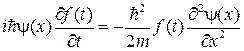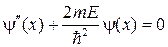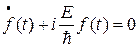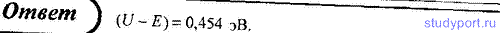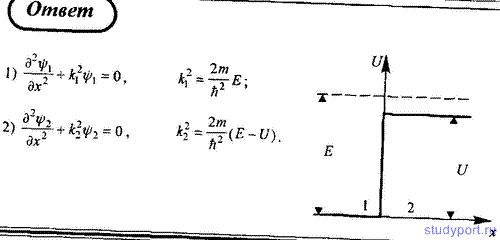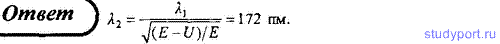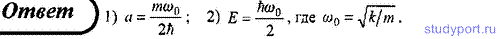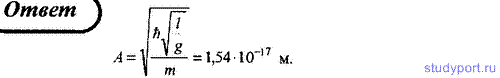Найти решение временного уравнения Шредингера для свободной частицы, движущейся с импульсом p в положительном направлении оси x.
Поскольку в данном случае потенциальная энергия частицы равна нулю U(x) = 0, то уравнение Шредингера будет иметь следующий вид:
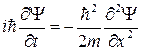
Решение данного уравнения будем искать методом разделения переменных, т.е. представим Y в виде произведения двух функций, одна из которых зависит только от координаты x, а другая – только от времени t.
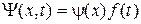
Подставляя (15) в (14) получим
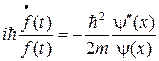
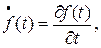
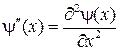
Т.к. обе части уравнения (16) являются функциями независимых переменных, то равенство правой и левой его частей возможно лишь тогда, когда они равны одной и той же константе. Из сравнения уравнения (16) со стационарным уравнением Шредингера можно видеть, что этой константой является E. Тогда
Общие решения данных дифференциальных уравнений должны иметь следующий вид (в этом нетрудно убедиться их непосредственной подстановкой):
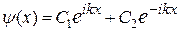
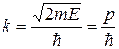
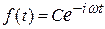
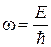
Тогда для частицы, движущейся в положительном направлении вдоль оси х, искомое решение уравнения (1) будет иметь вид
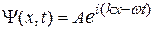
Данное решение будет конечным при Е > 0, причем Е в этом случае может быть любым. Волна, описываемая уравнением (17), имеет вид дебройлевской.
Плотность вероятности местоположения частицы 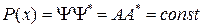
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Элементы квантовой механики
108. Электрон с энергией E = 5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите коэффициент D прозрачности потенциального барьера.
109. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определите в электрон-вольтах разность энергий U — E, при которой вероятность прохождения электрона сквозь барьер составит 0,5.
110. Протон с энергией E = 5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите вероятность прохождения протоном этого барьера. Во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях.
111. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U — E = 5 эВ. Определите, во сколько раз изменится коэффициент прозрачности D потенциального барьера для электрона, если разность U — E возрастает в 4 раза.
112. Частица с энергией E движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E > U. Запишите уравнение Шредингера для областей 1 и 2.
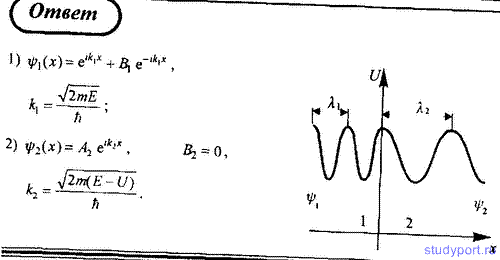
113. Для условия задачи 112 запишите решение уравнений Шредингера для областей 1 и 2. ψ -функция обычно нормируется так, что A1 = 1. Представьте графически качественный вид ψ -функций.
114. Частица с энергией E = 10 эВ движется в положительном направлении оси x, встречая на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 5 эВ. Определите коэффициент преломления n волн де Бройля на границе потенциального барьера.
115. Электрон с длиной волны де Бройля λ1 = 100 пм, двигаясь в положительном направлении оси x, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите длину волны де Бройля после прохождения барьера.
116. Частица с энергией E = 50 эВ, двигаясь в положительном направлении оси x, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 20 эВ. Определите вероятность отражения частицы от этого барьера.
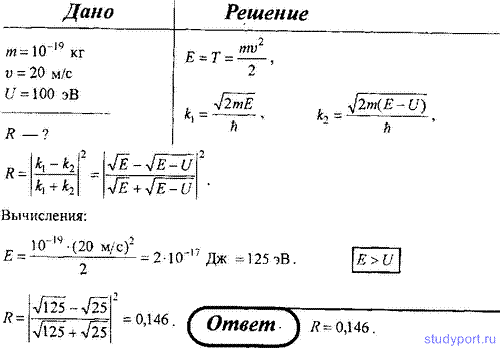
117. Частица массой m = 10 -19 кг, двигаясь в положительном направлении оси x со скоростью v = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите коэффициент отражения R волн де Бройля на границе потенциального барьера.
118. Частица с энергией Е движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E 2 обнаружения частицы в точке x = 0 области 2.
122. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E –корень( mk)/2 h* x^2 может быть решением уравнения Шредингера для гармонического осциллятора, масса которого m и постоянная квазиупругой силы k. Определите собственное значение полной энергии осциллятора.
124. Частица массой m движется в одномерном потенциальном поле U(x) = kx 2 /2 (гармонический осциллятор). Волновая функция, описывающая поведение частицы в основном состоянии, имеет вид ψ(x) = Ae — a x^2 , где A — нормировочный коэффициент; a—положительная постоянная. Используя уравнение Шредингера, определите: 1) постоянную a; 2) энергию частицы в этом состоянии.
126. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли.
127. Рассматривая математический маятник массой m = 100 г и длиной l = 0,5 м в виде гармонического осциллятора, определите классическую амплитуду A маятника, соответствующую энергии нулевых колебаний этого маятника.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Видео:Хренова М.Г. - Квантовая химия - 2. Атом водородаСкачать

«Волновые свойства частиц»
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
«ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ»
к решению задач по атомной физике
Методические указания разработаны кандидатом физико-математических наук, ассистентом кафедры нанотехнологии и кандидатом физико-математических наук, зав. кафедрой нанотехнологии .
Ответственный редактор канд. физ.-мат. наук
Компьютерный набор и верстка инженер
Печатается в соответствии с решением кафедры общей физики физического факультета РГУ, протокол от 01.01.01 г.
· Формула де Бройля, выражающая связь длины волны l с импульсом p движущейся частицы:
а) в классическом приближении (


б) в релятивистском случае (скорость v частицы сравнима со скоростью света с в вакууме 

· Связь длины волны де Бройля с кинетической энергией К частицы:
а) в классическом приближении 
б) в релятивистском случае 

· Соотношение неопределенностей Гейзенберга:
а) для координаты и импульса частицы 
б) для энергии и времени 
· В одномерном случае временное и стационарное уравнение Шредингера будут иметь вид


где i – мнимая единица, m – масса частицы; 
· Для случая трех измерений временное и стационарное уравнение Шредингера записывается в виде


где 
При решении уравнения Шредингера следует иметь в виду стандартные условия, которым должна удовлетворять волновая функция: конечность (во всем пространстве), однозначность, непрерывность самой Ψ – функции и ее производной.
· Вероятность P обнаружить частицу (в одномерном случае) в интервале от х1 до х2

· Коэффициент прозрачности D потенциального барьера U(x):

где х1 и х2 – координаты точек, между которыми U > E.
Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля l для двух случаев: 1) U1 = 51 В; 1) U2 = 510 кВ.
Длина волны де Бройля частицы зависит от ее импульса и определяется формулой

Связь импульса p с кинетической энергией К частицы для нерелятивистского (когда К 0, причем Е в этом случае может быть любым. Волна, описываемая уравнением (17), имеет вид дебройлевской.
Плотность вероятности местоположения частицы 
Частица массы m находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Показать, что собственные значения энергии частицы и ее нормированные собственные функции (0 частицы от центра.
Значение константы А найдем из условия нормировки пси-функции

где dV =4pr2dr– объем тонкого сферического слоя толщиной dr, находящегося на расстоянии r от центра. Тогда условие нормировки принимает вид


Как известно, среднее значение величины q, зависящей от координат

Тогда 
Частица массы m с энергией равной Е движется в положительном направлении оси х и встречает на своем пути бесконечно широкий потенциальный барьер высотой U., причем Е > U (рис.7) Для областей I и II: а) запишите уравнение Шредингера б) представьте графически качественный вид ψ – функций. Найти коэффициент отражения R и коэффициент прозрачности этого барьера.



На барьер падает частица массы m энергия которой Е, исходя из волновых представлений на барьер падает дебройлевская волна
Рис. 7 
Поскольку у всех трех волн (падающей, отраженной и прошедшей) частота одинакова, т. к.
Запишем уравнения Шредингера для областей I и II






Решением этих уравнений будут следующие функции:


Падающая волна характеризуется амплитудой a1, отраженная – b1 , прошедшая – а2. Поскольку в области x > 0 имеется только прошедшая волна, то b2 = 0.
Из условия непрерывности для y и y / в точке x = 0 следует


Решая совместно эти уравнения, получим



Обычно y — функция нормируется таким образом что а1 = 1, тогда

Качественный вид y — функций в областях I и II показан на рис. 8
Для определения интересующих нас коэффициентов отражения R и прозрачности D введем понятие потока плотности вероятности r. Скорость распространения вероятности такого потока совпадает со скоростью частицы

Таким образом v
k и плотность потока вероятности пропорциональна величине kψψ*. В соответствии с видом ψ – функции для падающей, отраженной и прошедшей волн имеем



Учитывая (26) получим следующие выражения для коэффициентов R и D:


Отсюда следует, что R + D = 1, что и должно быть по определению. Анализ выражений, полученных для R и D, показывает, что значения R и D не зависят от направления движения частицы. Заметим, что в классическом случае при Е>U R = 0.
Частица массы m падает слева на потенциальный барьер высотой U. (рис. 7). Энергия частицы равна Е, причем Е > U. Найти эффективную глубину хэф проникновения частицы под барьер, т. е. расстояние от границы барьера до точки, в которой плотность вероятности P нахождения частицы уменьшается в е раз. Вычислить хэф для электрона, если U — E = 1,0 эВ.
В данном случае вид уравнений Шредингера и ψ – функций будет совпадать со случаем, когда Е > U (см. задача №13 формулы (22) – (25)), однако k2, будет чисто мнимым

где i – мнимая единица, 
тогда плотность вероятности P(x) местоположения частицы в области II будет равна

Плотность вероятности нахождения частицы в точке х = 0


Качественный вид y — функций в областях I и II показан на рис. 8.
Т. к. эффективная глубина проникновения частицы определяется как расстояние, на котором плотность вероятности местонахож-
Рис. 8 дения частицы уменьшается в е раз то


Подставив численные значения, получим 
Частица с энергией Е = 50 эВ падает слева на прямоугольный барьер, бесконечной ширины высотой U = 20 эВ (рис 7). Определите вероятность отражения частицы от этого барьера.
Как было показано в предыдущей задаче, коэффициент отражения R равен

где k1 и k2 – волновые числа волн де Бройля в областях I и II.


Электрон с энергией Е = 4,9 эВ движется в положительном направлении оси х. Высота U потенциального барьера равна 5 эВ. При какой ширине барьера d вероятность P прохождения электрона через него будет равна 0,2?
Вероятность P прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности D. Тогда

Рис. 9 Так как для данного барьера (Рис. 9) U(x) = U, х1 = 0, х2 = d, то (27) примет вид

Потенцируя это выражение, получим


Произведя вычисления, получим d = 0.495 нм.
Найти вероятность прохождения частицы массой m с энергией Е сквозь потенциальный барьер, показанный на рис. 10.


В данном случае (рис.10)


Рис.10 тогда (28) примет вид

ОСНОВНЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ
Скорость света в вакууме
1. Иродов по квантовой физике: Учебное пособие для физ. спец. вузов. – М.: Высшая шк., 1991. – 175с.
2. Иродов физика. Основные законы: Учебное пособие для вузов. – М.: Лаборатория Базовых Знаний, 2001. – 271с.
3. , : Сборник задач по курсу физики с решениями: Учебное пособие для вузов. Изд. седьмое, стереотипное– М.: Высшая шк., 2006. – 591с.
4. Г, Воробьев по физике. Изд. пятое, переработанное и дополненное – М.: Высшая шк., 1988. – 527с.
5. Атомная физика. – М.: «Мир», 1970. – 483с.
6. Савельев общей физики. Т.3 — М.: Наука., 1982. – 304с.
7. Савельев вопросов и задач по общей физики. — М.: Наука, 1982. –271с.
💡 Видео
Урок 455. Уравнение ШрёдингераСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Уравнение ШрёдингераСкачать

Рубцов А. Н. - Введение в квантовую физику - Волновая функция и уравнение ШредингераСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Авакянц Л. П. - Введение в квантовую физику - Основы квантовой механикиСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

уравнение ШредингераСкачать

Корректный вывод уравнения Шрёдингера и его физический смысл: Липовка А.А. - Глобальная волнаСкачать

Урок 32. Уравнение ШрёдингераСкачать
Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ УРАВНЕНИЕ ШРЁДИНГЕРА | КОНДЕНСАТ (семинар) - КАЗАКОВ А. С. ФизФак МГУСкачать

Страупе С.С. - Введение в квантовую физику. Семинары - 6. Одномерное движение материальной точки.Скачать

Урок 454. Понятие о волновой функцииСкачать

Уравнение движенияСкачать

Квантовые числа. 1 часть. 10 класс.Скачать