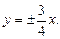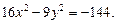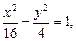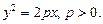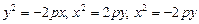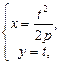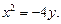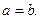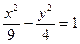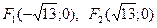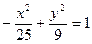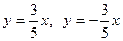Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Видео:Видеоурок "Гипербола"Скачать

Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Видео:§29 Эксцентриситет гиперболыСкачать

Задания для самостоятельного решения
I уровень
1.1. Определите характеристики (центр, полуоси, фокусы, эксцентриситет, уравнения директрис и асимптот) гиперболы 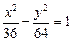
1.2. Составьте уравнение гиперболы, вершины которой находятся в точках A1(5, 0) и A2(5, 0), а расстояние между фокусами равно 14.
1.3. Составьте уравнение гиперболы, проходящей через точку М(2, 1) и имеющей асимптоты
1.4. Определите параметры гиперболы 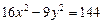
II уровень
2.1. Определите параметры (полуоси, координаты фокусов, эксцентриситет, уравнения директрис и асимптот) гиперболы
2.2 Составьте уравнение равносторонней гиперболы, зная ее фокус F(0, 1) и асимптоту x + y = 0.
2.3. Докажите, что уравнение определяет гиперболу, определите ее параметры и форму:
1) 16x 2 – 9y 2 – 64x – 54y – 161 = 0;
2) 9x 2 – 16y 2 + 90x + 32y – 367 = 0;
3) 16x 2 – 9y 2 – 64x – 18y + 199 = 0.
2.4. Убедившись, что точка A(–5; 9/4) лежит на гиперболе 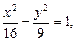
III уровень
3.1. Гипербола касается прямых 5x – 6y – 16 = 0, 13x – 10y – – 48 = 0. Запишите уравнение гиперболы при условии, что ее оси совпадают с осями координат.
3.2. Составьте уравнения касательных к гиперболе
1) проходящих через точку A(4, 1), B(5, 2) и C(5, 6);
2) параллельных прямой 10x – 3y + 9 = 0;
3) перпендикулярных прямой 10x – 3y + 9 = 0.
Парабола
Параболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
Параметры параболы:
Точка F(p/2, 0) называется фокусом параболы, величина p – параметром, точка О(0, 0) – вершиной. При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.
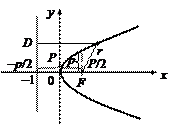 |
Величина 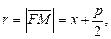
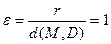
Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 24).
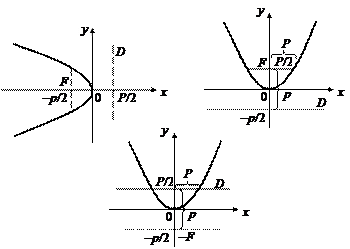
Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 25).:
 |
Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:
где t – произвольное действительное число.
Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:
1) 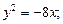
Решение.1. Уравнение y 2 = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y 2 = –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 26).
 |
2. Уравнение x 2 = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x 2 = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 27).
Пример 2.Определить параметры и вид кривой x 2 + 8x – 16y – 32 = 0. Сделать чертеж.
Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:
(x + 4) 2 – 16 – 16y – 32 =0;
В результате получим
Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх ( 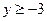
 |
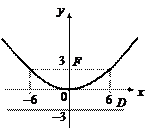
Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = 3 и точки F(0; 3).
Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x 2 = 2py с параметром p = 2 · 3 = 6, т. е. x 2 = 12y (рис. 29).
 |
Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Значит, искомое уравнение
(y + 2) 2 = –2 · 4(x – 3) или (y + 2) 2 = = –8(x – 3).
Видео:Асимптоты функции. 10 класс.Скачать

Равносторонняя гипербола
Дата добавления: 2015-08-31 ; просмотров: 3872 ; Нарушение авторских прав

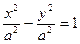
тогда уравнение равносторонней гиперболы имеет вид
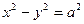
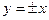
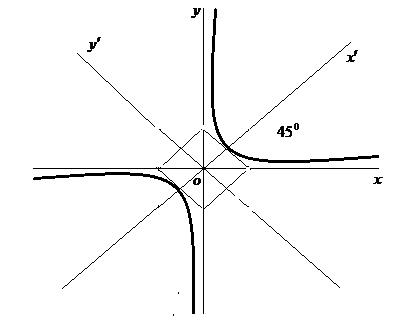
Из школьного курса известно, что уравнение гиперболы 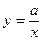
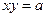
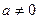
Можно доказать, если систему координат OXY повернуть на 45 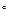
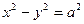
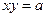
Поэтому про школьную гиперболу говорят – это равносторонняя гипербола, отнесенная к своим асимптотам.
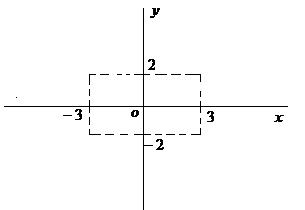
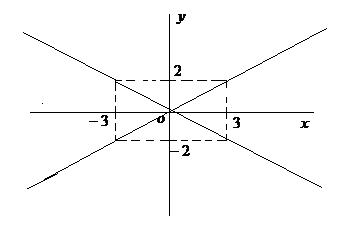
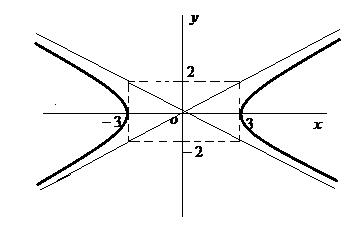
Задача 27Построить гиперболу 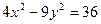
1 Запишем каноническое уравнение гиперболы, разделив обе части на 36, получим
2 Найдем полуоси гиперболы
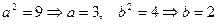
A(-3;0), C(3;0) – действительные вершины
B(0;2), D(0;-2) – мнимые вершины
4 Составим уравнения асимптот по формулам (4.4)
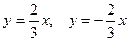
Выполним построение ( выполнить все этапы построения в одной системе координат) (рис.30)
1 этап – построить «основной» прямоугольник, по координатам вершин
2 этап – провести асимптоты ( диагонали прямоугольника)
3 этап – поострить гиперболу
Задача 28 Построить гиперболу 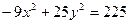
1 Запишем каноническое уравнение гиперболы, разделив обе части на 225, получим
2 Найдем полуоси гиперболы
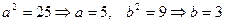
3 Координаты вершин:
A(-5;0), C(5;0) – мнимые вершины
B(0;3), D(0;-3) – действительные вершины
4 Уравнения асимптот:
📹 Видео
Фокусы гиперболыСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

ГиперболаСкачать

Математический анализ, 15 урок, АссимптотыСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Асимптоты функции. Наклонная асимптота. 10 класс.Скачать

Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

§23 Построение гиперболыСкачать

182 Алгебра 9 класс. Найдите Асимптоты гиперболы.Скачать

ГиперболаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Асимптоты графика функции. Практика. Пример 1.Скачать

Задание 10. ЕГЭ профиль. Горизонтальные и вертикальные асимптоты гиперболы.Скачать
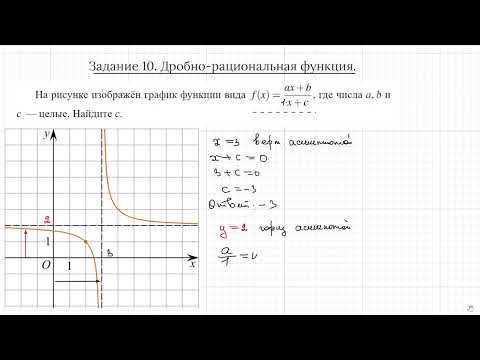
180 Алгебра 9 класс. Асимптоты. Укажите асимптоты гиперболыСкачать

§21 Каноническое уравнение гиперболыСкачать