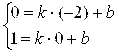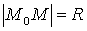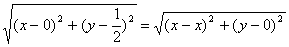Задание
Составить уравнение множества точек плоскости, равноудалённых от точки F (7; 3) и от прямой x — 2y = 11
Решение
Расстояние от точки А(x1, y1) до прямой Ax + By + C = 0 равно длине перпендикуляра, опущенного из этой точки на прямую.
Она определяется по формуле
Видео:9 класс, 7 урок, Уравнение прямойСкачать

d1 = (Ax1 + By1 + C)/(A^2 + B^2)^0.5 = (x1 — 2y1 — 11)/(5^0.5)
Расстояние d2 между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле
d2 = ((x2 — x1)^2 + (y2 — y1)^2)^0.5
Из условия равноудалённости следует, что d1 = d2
(x1 — 2y1 — 11)/(5^0.5) = ((x2 — x1)^2 + (y2 — y1)^2)^0.5
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Нужно возвести обе части в квадрат и привести подобные слагаемые
Получается квадратное уравнение, то есть геометрическим местом точек равноудалённых от заданной точи и прямой является парабола.
1.6. Первая основная задача аналитической геометрии на плоскости
Основных задач аналитической геометрии на плоскости две. Первая из них: Для заданной линии найти ее уравнение. Вторая задача – обратная: По заданному уравнению линии построить линию.
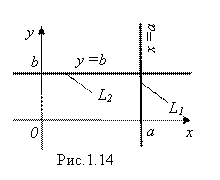
Пример 1. Найти уравнения вертикальной прямой L1 и горизонтальной прямой L2, изображенных на рис. 1.14.
Решение. Уравнения этих прямых очевидны: X= A – уравнение прямой L1, Y = B – уравнение прямой L2. Действительно, этим уравнениям удовлетворяют координаты любой точки соответствующих прямых, и только они. В частности, Y = 0 – это уравнение оси Ox, а X = 0 – уравнение оси Oy.
Видео:Составляем уравнение прямой по точкамСкачать

Пример 2. Найти уравнение прямой L, изображенной на рис. 1.15.
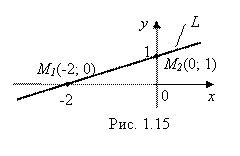
Используем рис. 1.15. Так как точки М1(-2; 0) и М2 (0; 1) лежат на прямой L, то их координаты (X; Y) должны удовлетворять уравнению прямой. Подставляя эти координаты в уравнение прямой Y = Kx + B, получим систему из двух равенств:
Решая ее, находим: 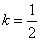
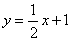
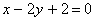
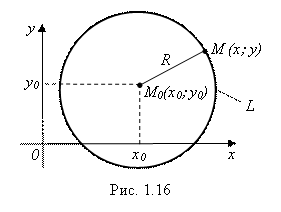
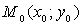
Решение. Для любой точки М(X; Y) окружности L, и только для точек этой окружности, имеет место равенство:
Реализуя это равенство с помощью формулы (3.1) расстояния между двумя точками, получим:
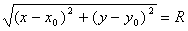
Возводя обе части этого равенства в квадрат, получим равносильное равенство:
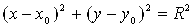
Видео:Найти точку на прямой, равноудалённую от двух данных точекСкачать

Это и есть искомое уравнение указанной окружности L.
В частности, если центр окружности совпадает с началом координат (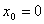
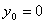
Это уравнение, кстати, совпадает с уравнением (4.11), полученным ранее другим путем.
Пример 4. Найти уравнение линии, состоящей из точек, равноудаленных от оси Ох и от точки 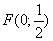
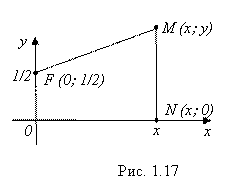
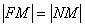
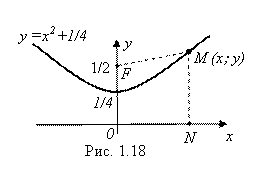
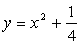
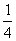
А теперь рассмотрим вопрос о Приближенных уравнениях линий. Чаще всего этот вопрос возникает, когда речь идет о линиях, полученных в результате экспериментов.
А именно, пусть экспериментальным путем изучается зависимость Y = F(X) между двумя величинами. Например, зависимость урожайности культуры Y от количества внесенных под нее удобрений X; пройденного пути Y от времени движения X; прибыли предприятия Y от величины затрат X и т. д. В ходе эксперимента для ряда значений X определяются соответствующие значения Y, что приводит к экспериментальной таблице вида
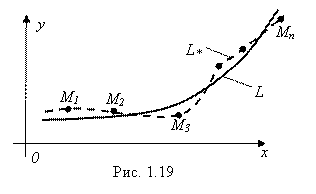
В этой задаче фактически идет речь о нахождении уравнения Y = F(X) линии L по точкам М1, М2, … МN, которые, вообще говоря, на этой линии не лежат, так как они содержат в себе неизбежные погрешности эксперимента и, кроме того, содержат результат влияния различных неучтенных факторов (помех). Поэтому искомая линия L может отличаться от линии L*, непосредственно соединяющей экспериментальные точки. В частности, линия L* может иметь весьма причудливую форму, в то время как сама линия L будет простой и гладкой (например, прямой). Линия L должна как бы сглаживать линию L*, устраняя ее незначительные перепады, связанные с неточным положением экспериментальных точек.
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

При нахождении эмпирической формулы Y = F(X), а значит, и соответствующей ей линии L, приходится решать две частные задачи.
Первая из них – выбор Типа эмпирической формулы. То есть выбор того класса функций, к которому принадлежит искомая функция Y = F(X). Во многих случаях класс функций, из которого подбирается эмпирическая формула, подсказывается теоретическими представлениями о характере изучаемой зависимости (зависимость линейная вида Y = Kx или Y = Kx + B, квадратичная вида 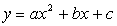
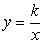
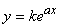
После того, как вид эмпирической формулы выбран, то есть первая частная задача решена, остается определить Наилучшие значения входящих в эту формулу числовых коэффициентов. Эта задача (вторая частная задача) уже более легкая, ибо решается стандартным методом – Методом наименьших квадратов. В соответствии с этим методом наилучшими значениями параметров эмпирической формулы считаются те, при которых сумма квадратов отклонений экспериментальных точек от эмпирической кривой Y = F(X) была бы минимальной.
Вручную реализовывать метод наименьших квадратов трудоемко, но это и не требуется – это обычно делается по стандартным программам на ЭВМ.
Впрочем, в простейшем (и наиболее часто встречающимся на практике) случае, когда экспериментальные точки располагаются приблизительно по прямой, можно обойтись и без метода наименьших квадратов – можно все сделать вручную, графическим путем.
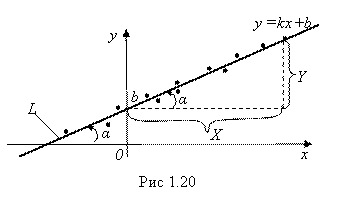
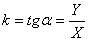
Кстати, этим путем можно построить и достаточно хорошие эмпирические формулы для ряда экспериментальных кривых – параболы, гиперболы и т. д., но на этом останавливаться не будем.
1. Написать уравнение прямой, проходящей через начало координат и точку 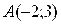
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

2. Написать уравнение линии, по которой движется точка М(x; y), равноудаленная от начала координат и от точки A(-4; 2). Лежат ли на этой линии точки B(-2;1), C(2;3), D(1;7)?
3. Найти уравнение линии, по которой движется точка, оставаясь постоянно вдвое ближе к оси Ох, чем к оси Оу. Построить линию по ее уравнению.
Ответ: 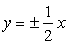
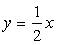
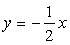
4. Найти уравнение линии, состоящей из таких точек, что разность расстояний от каждой из них до точек F1(-2;-2) и F2(2;2) равна 4. Построить линию по ее уравнению.
Ответ: 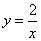
5. По данным эксперимента, представленным в таблице, графическим путем подобрать эмпирическую формулу вида Y = Kx + B.
🎥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой: метод трёх точекСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Уравнение параллельной прямойСкачать

Уравнение прямой на плоскости. Решение задачСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение прямой на плоскостиСкачать

Уравнение прямой по двум точкамСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать