Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
- Угол наклона прямой и угловой коэффициент прямой
- Уравнение с угловым коэффициентом
- Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
- Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
- Контрольная работа: Краткие сведения и задачи по курсу векторной и линейной алгебры
- Уравнение прямой с угловым коэффициентом
- 💡 Видео
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
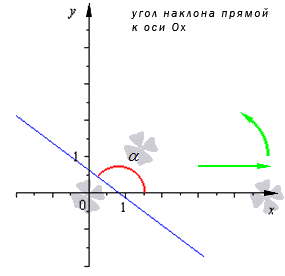
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
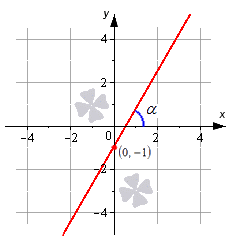
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Видео:Составляем уравнение прямой по точкамСкачать
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Видео:УЧИМСЯ ПОНИМАТЬ ЛИНЕЙНУЮ ФУНКЦИЮ. Уравнения прямой с угловым коэффициентом, по точкам и в отрезкахСкачать
Контрольная работа: Краткие сведения и задачи по курсу векторной и линейной алгебры
Краткие сведения и задачи по курсу векторной и линейной алгебры
Найти скалярное произведение 
.
При каком значении α векторы 
и 
ортогональны?
;
;
;
;
;
;
Два вектора ортогональны, когда их скалярное произведение равно нулю.
Для прямой М 1 М 2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М 1 (0,-3) М 2 (2,1).
Общий вид уравнения прямой с угловым коэффициентом записывается в виде:
значит для прямой М 1 М 2
Общий вид уравнения прямой, проходящей через две точки записывается в виде:
,
значит для прямой М 1 М 2
Общий вид уравнения прямой в отрезках записывается в виде:
,
Уравнения прямой в отрезках для прямой М 1 М 2
;
В треугольнике М 0 М 1 М 2 найти уравнение медианы, высоты, проведенных их вершины М 0 , а также уравнение средней линии EF, параллельной основанию М 1 М 2 .(М 0 (-1,-2); М 1 (0,-3); М 2 (2,1)).
Найдём координаты точки М 3 , координаты середины стороны М 1 М 2 :
уравнения прямой, проходящей через две точки записывается в виде:
,
уравнение для высоты М 0 М 3 :
Найдём уравнение прямой М 1 М 2 :
Из условия перпендикулярности (k 2 =-1/k 1 ) следует, что k 2 =1/2.
Уравнения прямой с угловым коэффициентом записывается в виде:
тогда уравнение для высоты примет вид:
Расстояние от точки М(x 0 ,y 0 ) до прямой Ax+By+c=0 находится по формуле:
Чтобы найти длину высоту, найдём расстояние от точки М 0 (-3,-5) до прямойМ 1 М 2 , уравнение которой имеет вид -x+2y-4=0. Подставим данные в формулу(1):
Найдём координаты точек Е иF.
Для точки Е: x=-1/2; y=-5/2; E(-1/2;-5/2).
Для точки F: x=1/2; y=-1/2; F(1/2;-1/2).
Уравнение прямой EF:
y+5/2=-2x-1 или 2x+y+3,5=0.
По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).
(1)
Воспользуемся параллельным переносом (O’(-3,-1))
(2)
Подставим (2) в (1), получим
кривая второго порядка является эллипсом.
т.к.
Координаты центра: O’(-3,-1).
Преобразовать к полярным координатам уравнения линии.
1)
2) 
Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:
Ответы на вопросы
Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную 
.
Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Система уравнений в матрично-векторной форме записывается в виде: 
.
Решение системы уравнения при помощи обратной матрицы:
Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?
Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:
Выполняются элементарные преобразования, вследствие чего можно получить два исхода:
получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;
система приводится к лестничному виду.
Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.
Если число уравнений меньше чем число неизвестных, то решений бесконечное множество. В этом случае неизвестные разделяются на зависимые и свободные. Число зависимых неизвестных совпадает с числом уравнений.
т.к. detA
0, то матрица является невырожденной.
А 11 =3;А 12 = -1;А 13 = -10;А 21 =0;А 22 =0;А 23 = -1;А 31 =0;А 32 = -1;А 33 = -1.
;
.
.
.
5. Найти скалярное произведение .
При каком значении α векторы и ортогональны?
;
;
;
;
;
;
Два вектора ортогональны, когда их скалярное произведение равно нулю.
Для прямой М 1 М 2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М 1 (2,-2) М 2 (1,0).
Общий вид уравнения прямой с угловым коэффициентом записывается в виде:
значит для прямой М 1 М 2
Общий вид уравнения прямой, проходящей через две точки записывается в виде:
,
значит для прямой М 1 М 2
Общий вид уравнения прямой в отрезках записывается в виде:
,
здесь
Уравнения прямой в отрезках для прямой М 1 М 2
;
В треугольнике М 0 М 1 М 2 найти уравнение медианы, высоты, проведенных их вершины М 0 , а также уравнение средней линии EF, параллельной основанию М 1 М 2 .(М 0 (-3,-5); М 1 (2,-2); М 2 (1,0)).
Найдём координаты точки М 3 , координаты середины стороны М 1 М 2 :
уравнения прямой, проходящей через две точки записывается в виде:
,
уравнение для высоты М 0 М 3 :
Найдём уравнение прямой М 1 М 2 :
Из условия перпендикулярности (k 2 =-1/k 1 ) следует, что k 2 =-1/2.
Уравнения прямой с угловым коэффициентом записывается в виде:
тогда уравнение для высоты примет вид:
Расстояние от точки М(x 0 ,y 0 ) до прямой Ax+By+c=0 находится по формуле:
Чтобы найти длину высоту, найдём расстояние от точки М 0 (-3,-5) до прямойМ 1 М 2 , уравнение которой имеет вид 2x+y-2=0. Подставим данные в формулу(1):
Найдём координаты точек Е иF.
Для точки Е: x=-1/2; y=-7/2; E(-1/2;-7/2).
Для точки F: x=-1; y=-5/2; F(-1;-5/2).
Уравнение прямой EF:
y+7/2=-2x-1 или 2x+y+4,5=0.
По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).
(1)
Воспользуемся параллельным переносом (O’(-2,2))
(2)
Подставим (2) в (1), получим
кривая второго порядка является эллипсом.
т.к.
Координаты центра: O’(-2,2).
Преобразовать к полярным координатам уравнения линии.
1) 
2) 
Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс,. Поэтому первое уравнение можно отбросить. Следовательно получаем:
Ответы на вопросы
Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную .
Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Система уравнений в матрично-векторной форме записывается в виде:
.
Решения системы уравнения при помощи обратной матрицы:
Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?
Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:
Выполняются элементарные преобразования, вследствие чего можно получить два исхода:
получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;
система приводится к лестничному виду.
Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.
Если число уравнений меньше чем число неизвестных, то решений бесконечное множество. В этом случае неизвестные разделяются на зависимые и свободные. Число зависимых неизвестных совпадает с числом уравнений.
r=2; система совместима.
х 3,x 4 – свободные переменные
;
.
т.к. detA0, то матрица невырождена.
А 11 =-1; А 12 =-3; А 13 =-1;А 21 =-3;А 22 =1;А 23 =2;А 31 =2;А 32 =-1;А 33 = -3.
.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Уравнение прямой с угловым коэффициентом
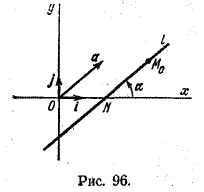
Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М0 параллельно направляющему вектору а (рис. 96).
Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l. (Имеется в виду угол, меньший 180°.)
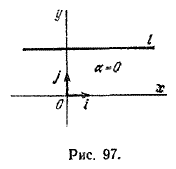
Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох, то угол наклона принимается равным нулю (рис. 97).
Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k:
Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.
Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу), не имеет углового коэффициента.
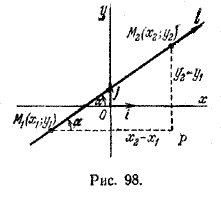
Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M1(x1; у1) и M2(x2; у2) и пусть, например, 0 x1, у2 > у1 (рис. 98).
Тогда из прямоугольного треугольника M1РM2 находим
Аналогично доказывается, что формула (2) верна и в случае 90° 3 х + 3у — 7 = 0.
Приведем данное уравнение к виду
Следовательно, k = tg α = — 1 /√ 3 , откуда α = 150°
Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = 2 /5
Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.
Если α = 30°, то k = tg 30° = √ 3 /3. Подставив в уравнение (4) значения x1, y1 и k, получим
💡 Видео
Угловой коэффициент прямойСкачать
Уравнение прямой на плоскостиСкачать
Угловой коэффициент прямой. Решение задач.Скачать
Видеоурок "Уравнение прямой, проходящей через две точки"Скачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
9 класс, 7 урок, Уравнение прямойСкачать
Уравнения стороны треугольника и медианыСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Видеоурок "Общее уравнение прямой"Скачать
§11 Уравнение прямой, проходящей через две точки на плоскостиСкачать
Уравнение прямой линии с угловым коэффициентом проходящей через точкуСкачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
Уравнение прямой на плоскости. Решение задачСкачать
