- УСЛОВИЕ:
- РЕШЕНИЕ:
- ОТВЕТ:
- Решения пользователей
- РЕШЕНИЕ ОТ vk54215494
- Написать комментарий
- 1 ответ
- Онлайн калькулятор. Угол между плоскостями.
- Найти угол между плоскостями
- Ввод данных в калькулятор для вычисления угла между плоскостями
- Дополнительные возможности калькулятора вычисления угла между плоскостями
- Теория. Угол между плоскостями
- Двугранные углы. Углы между плоскостями. Перпендикулярность плоскостей
- 🔥 Видео
УСЛОВИЕ:
Составьте уравнения плоскостей делящих пополам двугранные углы, образованные плоскостями x-2y+2z+6=0 и 4x+2y-4z+5=0
РЕШЕНИЕ:
ОТВЕТ:
Добавил slava191 , просмотры: ☺ 11785 ⌚ 05.01.2015. математика 1k класс
Решения пользователей
РЕШЕНИЕ ОТ vk54215494
«..Мы всю левую часть умножили на 2.»
для чего, почему и всегда ли так нужно делать?
Написать комментарий
Делим обе части равенства на π
и умножаем на 4
+pi k, k in Z
Можно правую часть записать в виде двух ответов:
x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].
x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]
[b]x=-5 – наибольшее отрицательное [/b]
О т в е т. x=1+8n in Z или x=3+ 8n, n in Z
корни чередуются так:
. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .
[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)
a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член
4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0
5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.
∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.
складываем оба равенства:
2* ∠ А=126 градусов.
По формулам приведения:
sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1
sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1
sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z
Найдем корни, принадлежащие указанному отрезку с помощью неравенства:
-286 ° ≤ 90 ° +360 ° *k ≤ 204 °
-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °
-376 ° ≤ 360 ° *k ≤ 114 °
Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]
Значит, указанному отрезку принадлежат два корня:
x=90 ° +360 °* ([green]-1[/green])=-270 °
x=90 ° +360 °*[red]0[/red]=90 °
7. KT- средняя линия трапеции:
Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)
Высоты треугольников АКО и СОК равны половине высоты трапеции
S_( Δ АКО)+S_( Δ COK)=44
S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=
О т в е т. [b]176[/b]
B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды
Задание: cоставить уравнение плоскости(u), делящей пополам острый двугранный угол, образованный плоскостью(p1) 3x-4y+6z-2=0 с координатной плоскостью Oyz.
Окей, вторая плоскость(p2) получается задается уравнением By+Cz=0. Произвольная точка М(x0,y0,z0) принадлежит искомой плоскости только тогда, когда d(M,p1)=d(M,p2), то есть расстояния от точки, до заданных плоскостей плоскостей одинаковые, составила уравнение: $$ frac > = frac + C^ > > $$
Ответ должен быть(дан в пособии) $$ (3-sqrt )x-4y+6z-2=0$$ что явно не получится из того уравнения, что я составила. Как можно решить данную задачу?
задан 19 Окт 19:58
Условие надо хотя бы верно записывать. Наверняка так:
Угол, образованный плоскостью $% ; (p1): 3x-4y+6z-2=0 ;$% с координатной плоскостью $%Oyz$%.
@KristinaM: вторая плоскость, то есть Oyz, задаётся уравнением x=0. Поэтому никаких B, C там нет, а будет просто |x|. Тогда после раскрытия модулей возникнут две плоскости. Одна — та, что из ответа. Другая — ей перпендикулярная. По идее, там надо распознать, какая именно из этих плоскостей подходит, то есть какие углы будет острыми. Это легко проверить при помощи рассмотрения векторов нормали к плоскостям и их скалярных произведений.
К слову сказать, By+Cz=0 есть семейство плоскостей, проходящих через ось Ox.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

1 ответ
Нормали к плоскостям равной длины: $%;vec =(3; -4; 6); ; vec =(sqrt ; 0; 0),;$% угол между которыми острый. Тогда нормаль к биссекторной плоскости: $% ; vec =(3+sqrt ; -4; 6);-$% сумма нормалей.
Стало быть, уравнение: $%; (3+sqrt )x -4y+ 6z-2=0, ;$% учитывая точку $%(0; 1; 1)$%.
Для того, чтобы оценить ресурс, необходимо авторизоваться.
В учебно-методическом пособии излагаются теоретические основы аналитической геометрии в пространстве, приводятся решения большого числа задач. Пособие содержит варианты задач (с ответами) для самостоятельного решения, список формул и рекомендуемой литературы. Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов строительных специальностей направления 6533500 «Строительство» всех форм обучения. Подготовлено кафедрой высшей математики УГТУ-УПИ.
Видео:Двугранный угол. Признак перпендикулярности плоскостей. Видеоурок 10. Геометрия 10 классСкачать

Онлайн калькулятор. Угол между плоскостями.
Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между плоскостями.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между плоскостями и закрепить пройденный материал.
Видео:10 класс - Геометрия - Двугранный уголСкачать

Найти угол между плоскостями
Уравнение 1-ой плоскости:
Уравнение 2-ой плоскости:
Ввод данных в калькулятор для вычисления угла между плоскостями
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления угла между плоскостями
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Угол между плоскостями
Двугранный угол между плоскостями равен углу образованному их нормальными векторами.
Если заданы уравнения плоскостей A1 x + B1 y + C1 z + D1 = 0 и A2 x + B2 y + C2 z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α = | |A1·A2 + B1·B2 + C1·C2| |
| √ A1 2 + B1 2 + C1 2 √ A2 2 + B2 2 + C2 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Двугранные углы. Углы между плоскостями.
Перпендикулярность плоскостей
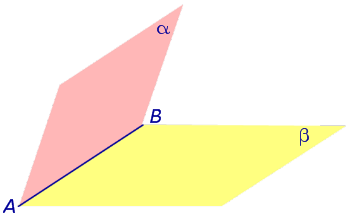
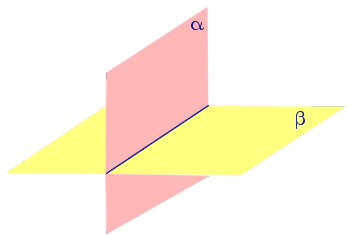
Двугранным углом называют часть пространства, ограниченную двумя полуплоскостями с общей границей (рис. 1)
Полуплоскости α и β , ограничивающие двугранный угол, называют гранями двугранного угла , а их общую границу AB называют ребром двугранного угла .
Двугранные углы называют равными двугранными углами , если их можно совместить.
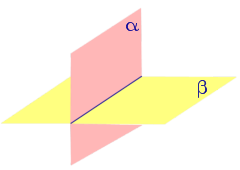
При пересечении двух плоскостей образуются четыре двугранных угла (рис. 2). Наименьший из этих углов обычно и называют углом между плоскостями .
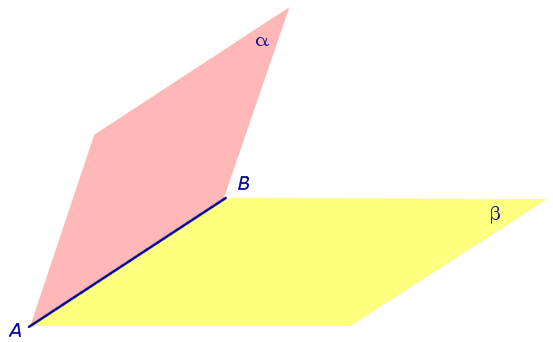
Если при пересечении двух плоскостей образовалось 4 равных двугранных угла, то такие двугранные углы называют прямыми двугранными углами , а сами плоскости называют перпендикулярными плоскостями (рис. 3).
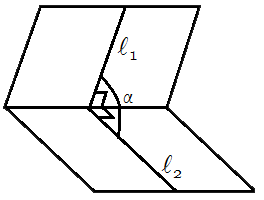
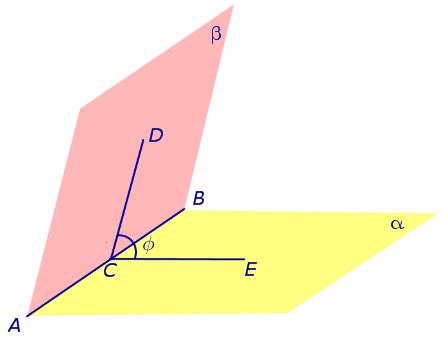
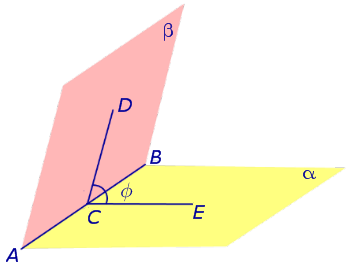
Выберем произвольную точку С на ребре AB двугранного угла и проведем через нее перпендикуляры CD и CE в каждой из граней двугранного угла. Угол DCE , образованный перепендикулярами CD и CE, называют линейным углом двугранного угла (рис. 4).
На рисунке 4 угол φ является линейным углом двугранного угла с гранями α и β и ребром AB .
Линейные углы двугранных углов используются, в частности, для того, чтобы измерять двугранные углы. Например, если линейный угол двугранного угла равен 30° ( или 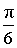
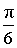

🔥 Видео
Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать

Геометрия 10 класс (Урок№11 - Перпендикулярность плоскостей.)Скачать

Уравнение плоскости. 11 класс.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

11 класс, 8 урок, Уравнение плоскостиСкачать

Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Перпендикулярность плоскостей - определениеСкачать

Двугранный уголСкачать

Уравнение плоскости. Практическая часть. 11 класс.Скачать

№174. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и ACB прямые, ACСкачать

Видеоурок "Общее уравнение плоскости"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать