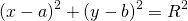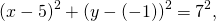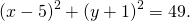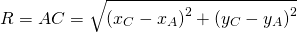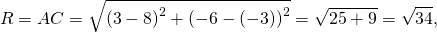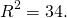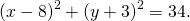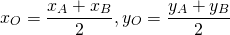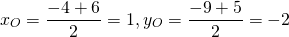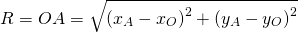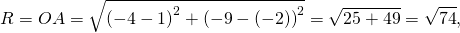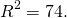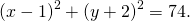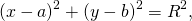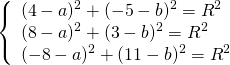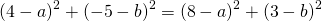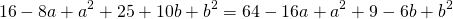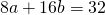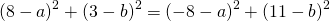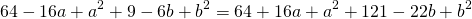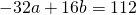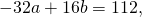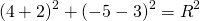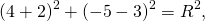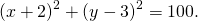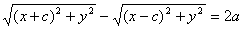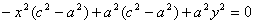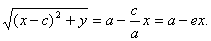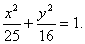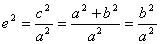Написать уравнение окружности имеющей центр в фокусе параболы y 2px и окружности (2 видео)

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Видео:Уравнение окружности (1)Скачать

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Решение аналогично решению задания 4. В результате получим уравнение

Написать уравнение окружности имеющей центр в фокусе параболы y 2px и окружности

Ах 2 + 2Вху + Су 2 + 2 Dx + 2 Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) — уравнение эллипса.

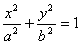
2) — уравнение “мнимого” эллипса.

3) — уравнение гиперболы.

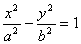
4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2 px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

8) y 2 = 0 – пара совпадающих прямых.

9) ( x – a ) 2 + ( y – b ) 2 = R 2 – уравнение окружности.

В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

2 x 2 + 2 y 2 – 8 x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4 x + 2,5 y – 2 = 0

x 2 – 4 x + 4 –4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0

( x – 2) 2 + ( y + 5/4) 2 – 25/16 – 6 = 0

( x – 2) 2 + ( y + 5/4) 2 = 121/16

Отсюда находим О (2; -5/4); R = 11/4.

Определение. Эллипсом называется линия, заданная уравнением .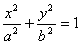

О пределение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

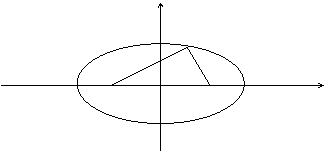
с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

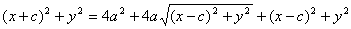
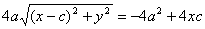
Доказательство: В случае , если точка М находится на пересечении эллипса с вертикальной осью, r ₁ + r ₂ = 2 (по теореме Пифагора). В случае , если точка М находится на пересечении эллипса с горизонтальной осью, r ₁ + r ₂ = a – c + a + c . Т.к. по определению сумма r ₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a 2 = b 2 + c 2

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Определение. Величина k = b / a называется коэффициентом сжатия эллипса, а величина 1 – k = ( a – b )/ a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

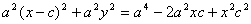
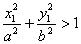
Если для точки М( х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М( х , у), принадлежащей эллипсу верны соотношения:

r ₁ = a – ex , r ₂ = a + ex .

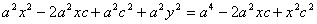
Доказательство. Выше было показано, что r ₁ + r ₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r ₂ = a + ex . Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

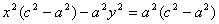
x = a / e ; x = — a / e .

Теорема. Для того , чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F ₂ (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Видео:Составляем уравнение окружностиСкачать

Пример. Составить уравнение эллипса, если его фокусы F ₁ (0; 0), F ₂ (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: 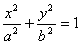. Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .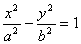

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

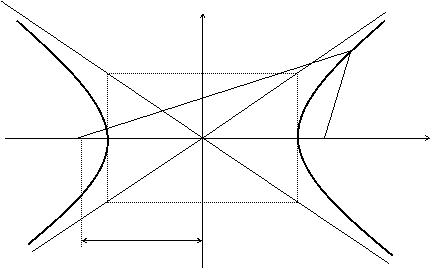
По определению ï r ₁ – r ₂ ï = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М( х , у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение 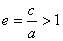называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2 :

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a / e от него, называются директрисами гиперболы. Их уравнения: .

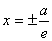
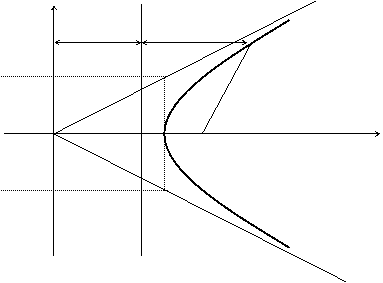
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.