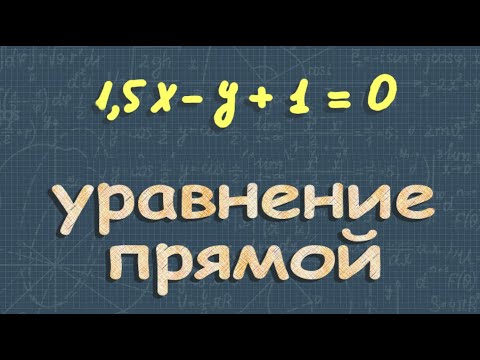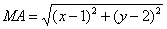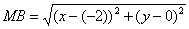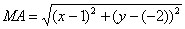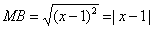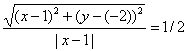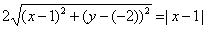Написать уравнение множества точек удаленных от прямой 4x 3y 0 на 4 единицы

Дана прямая 4x + 3y + 1 = 0. Найти уравнение прямой, параллельной данной и отстоящей от нее на 3 единицы.

Очевидно, что искомых прямых будет две. Отклонение точек одной из искомых прямых от данной будет равно +3, а другой -3; .

Уравнение семейства прямых, параллельных данной, будет таким:

Из этого семейства требуется отобрать две искомые прямые. После приведения его к нормальному виду получим

(два знака в знаменателе мы удерживаем пока потому, что знак C нам неизвестен). Возьмем на данной прямой произвольную точку, например, . Подставим ее координаты в левую часть последнего уравнения и, учитывая, что отклонение точек данной прямой от искомых равно , для определения C получим уравнение

, откуда

Четыре случая: сводятся к двум: , откуда C₁ = 16; C₂ = -14. Подставляя эти значения C в уравнение семейства прямых 4x + 3y + C = 0, получим, что искомых прямых две:

4x + 3y + 16 = 0 и 4x + 3y — 14 = 0.

Решение допускает простую проверку, которую рекомендуется сделать.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Множество точек на плоскости

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как


то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:


то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составить уравнение геометрического места точек одинаково удаленных

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему нахождения геометрического места точек (ГМТ) по определенным условиям: удаленности от начала координат или произвольных точек, удаленности от кривых и прямых и т.п.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Геометрическое место точек: решения онлайн

Задача 1. Написать уравнение геометрического места точек, удаленных от прямой $х + 2у – 5 = 0$ на расстояние $sqrt $.

Задача 2. Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки $(5;0)$ относятся как $2:1$.

Задача 3. Составить уравнение множества точек, для каждой из которых выполняется следующее условие: квадрат расстояния до точки $A(2,0)$ на 16 больше квадрата расстояния до оси ординат.

Задача 4. Составить уравнение линии, для каждой точки которой расстояние от точки $A(0,1)$ вдвое меньше расстояния от прямой $y=4$.

Задача 5. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек $A(-3,0)$ и $B(0,3)$ равна 26. Построить эту линию.

Задача 6. Составить уравнение геометрического места точек, отношение расстояний которых до данной точки $A(2;0)$ и до данной прямой $x=4,5$ равно числу $2/3$. Полученное уравнение привести к простейшему виду и затем построить кривую.

Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку F(2;-4); ox– ось симметрии.

Ответ: .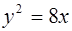

Задача 67.

Составить уравнение геометрического места точек, одинаково удаленных от точки F(2;0) и от прямой .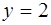

Ответ: .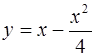

Задача 68.

Составить каноническое уравнение параболы, если ее фокус находится в точке пересечения прямой 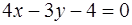с осью 0х.

Ответ: .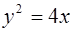

Задача 69.

На параболе 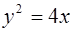найти точку, фокальный радиус которой равен 4.

Ответ: , .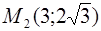

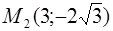
Задача 70.

Написать уравнение окружности, проходящей через начало координат и точки пересечения параболы 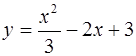с осями координат.

Ответ: .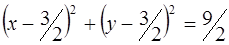

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8921 – | 7229 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение геометрического места точек, одинаково удаленных от точки F(0,2) и от прямой y=4. Найти точки пересечения этой кривой с осями координат и построить её

задан 23 Дек ’13 19:51

Надо приравнять квадраты расстояний от точки то точки, то есть $%x^2+(y-2)^2$%, и от точки до прямой, то есть $%(y-4)^2$%. После упрощений получится уравнение параболы. Остальное просто.

Здравствуйте

Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

📹 Видео

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Составляем уравнение прямой по точкамСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Множества и операции над нимиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Геометрия 9 класс. Тема: "Уравнение прямой".Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Множества. Операции над множествами. 10 класс алгебраСкачать

9 класс, 2 урок, Множества и операции над нимиСкачать

№975. Найдите координаты точек пересечения прямой 3x-4y + 12 = 0 с осями координатСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

УРАВНЕНИЕ ПРЯМОЙСкачать