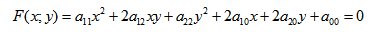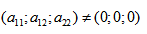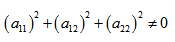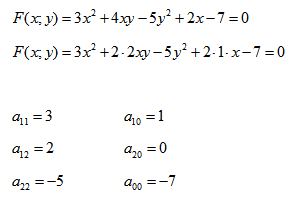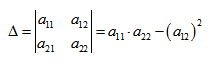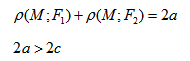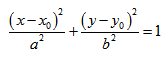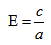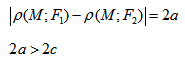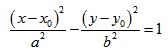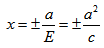Линии второго порядка
1. Основные понятия.
6. Общее уравнение линий второго порядка.
ОСНОВНЫЕ ПОНЯТИЯ
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел 
ОКРУЖНОСТЬ
Простейшей кривой второго порядка является окружность.
Определение. Окружностью радиуса R с центром в точке 


Каноническое уравнение окружности 
Эллипс
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Каноническое уравнение эллипса 

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.



Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
Определение.Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: 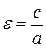
Замечание. Для эллипса 
Определение.Прямые 
Теорема. Если 
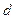


Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.
Если же 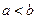



Пример. Составьте уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), а большая ось равна 2.
Уравнение эллипса имеет вид: 
Расстояние между фокусами: 2c = 
a 2 – b 2 = c 2 = 
По условию большая ось равна 2, то есть 2а = 2, откуда получаем, что
а = 1, b = 
Тогда искомое уравнение эллипса имеет вид: 
Гипербола
Определение. Гиперболойназывается линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы 

Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:
Ось 2а называется действительной осью гиперболы.
Ось 2b называется мнимой осью гиперболы.
Прямоугольник со сторонами 2а и2b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты, уравнения которых
Замечание.Для гиперболы эксцентриситет 
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы. Их уравнения: 
Определение. Гипербола называется равносторонней, если ее полуоси равны ( 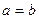
Ее каноническое уравнение 
Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается 

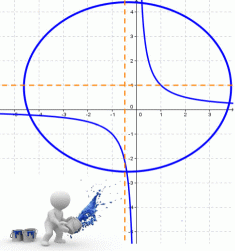
Кривая, определяемая уравнением 



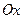
Гиперболы 

Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением
Найдем фокусное расстояние для эллипса:
Тогда искомое уравнение гиперболы 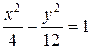
Парабола
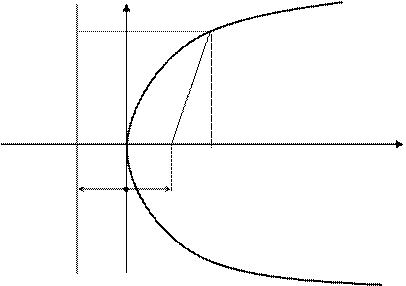
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы y 2 = 2px .
- Кривые второго порядка — определение и построение с примерами решения
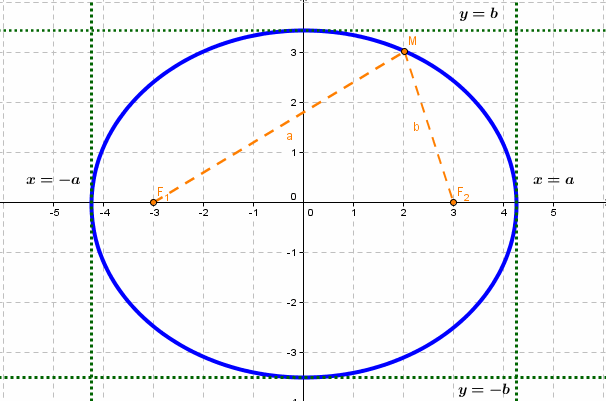
- Эллипс
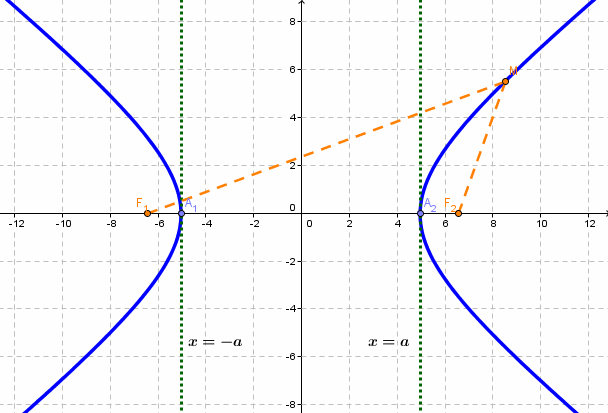
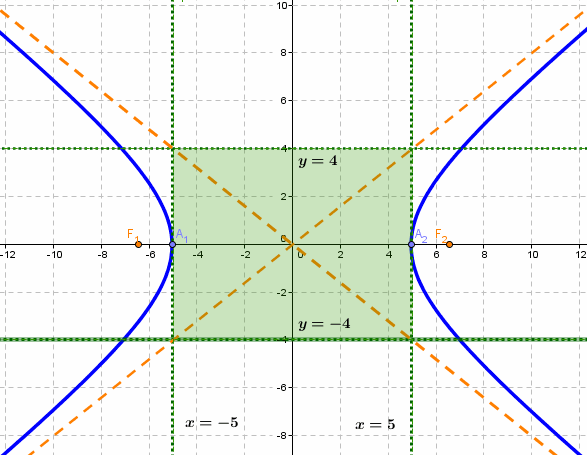
- Гипербола
- Кривые второго порядка на плоскости
- Кривые второго порядка
- Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
- Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
- Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
- Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
- 📸 Видео
Видео:Видеоурок "Гипербола"Скачать

Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Видео:213. Фокус и директриса параболы.Скачать

Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Кривые второго порядка
Видео:Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Видео:Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

или можно встретить следующую форму записи:
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Видео:Фокус и директриса параболы 1Скачать

Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ F1 и F2 — фокусы.
 |
 |
 | 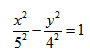 |
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
📸 Видео
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

§28 Эксцентриситет эллипсаСкачать

кривые второго порядка (решение задач)Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

165. Найти фокусы и эксцентриситет эллипса.Скачать

Видеоурок "Парабола"Скачать