Написать уравнение кривой по которой движется точка m если расстояние (7 видео)

3.1. Линии второго порядка. Каноническое уравнение эллипса

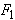
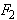
Определение. Эллипсом называется геометрическое место точек плоскости для которых сумма расстояний до двух фиксированных точек и , называемых фокусами, есть величина постоянная.

Выведем уравнение эллипса в соответствии с данным определением. Для этого зафиксируем декартову систему координат ХОу как показано на рисунке.

Согласно определению эллипса для точки М имеем , где А — некоторая постоянная. В координатах

Подставим эти значения в основное равенство, получим уравнение

После стандартного метода «уничтожения» радикалов (возведения обеих частей уравнения в квадрат (см. пример 1.)) получим каноническое уравнение эллипса

(1)

Где . Величины А и B, называются соответственно Большой и Малой Полуосями эллипса.

Замечание. В частности, при из (1) имеем уравнение окружности радиуса А с центром в начале координат

. (2)

1. Эллипс имеет две взаимно перпендикулярные оси симметрии Х и У (их называют главными осями эллипса) и центр симметрии О (его называют центром эллипса).

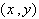
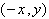
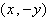
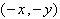
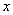
Утверждение следует из того, что замена координат на или или не изменяет вид уравнения (1). При этом, в первом случае, при преобразовании , имеем ось симметрии У, во втором — ось симметрии , а в третьем — центр симметрии О.

2. Эллипс полностью содержится в прямоугольнике

Из уравнения (1) имеем . Аналогично, .

3. Эллипс получается равномерным сжатием окружности.

Рассмотрим окружность . Произведем равно-мерное сжатие плоскости к оси Ох: . Подставим эти значения в уравнение окружности (2), имеем . После деления на получим уравнение (1).

Построим эллипс на основании его свойств и уравнения (1)

Пример 1. Написать уравнение кривой по которой движется точка M, если сумма расстояний от нее до точек и остается постоянной и равной .

Решение. Согласно условию задачи

Возведем обе части уравнения в квадрат и приведем подобные члены, получим

Еще раз возводим в квадрат и приведем подобные члены

Пример 2. На эллипсе найти точку, расстояние от которой до фокуса в четыре раза больше расстояния чем до фокуса .

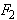
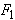
Решение. Запишем уравнение эллипса в каноническом виде:

Найдем координаты фокусов эллипса

Согласно условию задачи

Выразим Из уравнения эллипса , подставим в данное уравнение и приведем подобные члены, получим квадратное уравнение Его корни — лишний корень, т. к. . Тогда . Отв.

Содержание

Задача 26616 4.1.80) Написать уравнение кривой, сумма.
Условие
Решение
Кривые второго порядка
📸 Видео

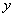
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Задача 26616 4.1.80) Написать уравнение кривой, сумма.

Условие

4.1.80) Написать уравнение кривой, сумма расстояний от каждой точки которой до точек F1(-2; 0) и F2(2; 0) равна 2sqrt(5)

Решение

Пусть M(x;y) — произвольная точка кривой.
F_(1)M=sqrt((x-(-2))^2+(y-0)^2)=sqrt((x+2)^2+y^2);
F_(2)M=sqrt((x-2)^2+(y-0)^2)=sqrt((x-2)^2+y^2);
По условию
F_(1)M+F_(2)M=2sqrt(5)

Возводим в квадрат.

x^2+4x+4+y^2=20-2*2sqrt(5)sqrt((x-2)^2+y^2)+x^2-4x+4+y^2
4sqrt(5)*sqrt((x-2)^2+y^2)=20-8x;
sqrt(5)*sqrt((x-2)^2+y^2)=5-2x
Возводим в квадрат
5*((x-2)^2+y^2)=25 — 20x+4x^2
5x^2- 20x+20+y^2=25 — 20x + 4x^2
x^2 +5 y^2=5
(x^2/5)+y^2=1 — уравнение эллипса
с полуосями a=sqrt(5) и b=1

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка

8.1. Написать уравнение окружности с центром С(-4;3), радиусом R=5 и построить ее. Лежат ли на этой окружности точки А(-1;-1), В(3;2), О(0;0)?

Ответ: А иО – на окружности, В – вне ее.

8.2. Построить окружности: 1) х 2 +у 2 -4х+6у-3=0; 2) х 2 +у 2 -8х=0; 3) х 2 +у 2 +4у=0.

8.3. Построить эллипс х 2 +4у 2 =16, найти его фокусы и эксцентриситет.

Ответ:

8.4. Построить эллипс 9х 2 +25у 2 =225. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнение директрис.

8.5. Написать каноническое уравнение эллипса, если: а) а=3, b=2; б) а=5, с=4; в) с=3, е=3/5; г) b=5, е=12/13; д) с=2 и расстояние между директрисами равно 5; е) е=1/2 и расстояние между директрисами равно 32.

Ответ: а) ; б) ; в) ; г) ; д) ; е) .

8.6. Написать каноническое уравнение эллипса, зная, что: 1) расстояние между фокусами равно 8, а малая полуось b=3;2) большая полуось а=6, а эксцентриситет е=0,5.

Ответ: 1) 2)

8.7. Земля движется по эллипсу, в одном из фокусов которого находится Солнце. Наименьшее расстояние от Земли до Солнца равно приблизительно 147,5 млн км, а наибольшее 152,5 млн км. Найти большую полуось и эксцентриситет орбиты Земли.

Ответ: а=150 млн км,

8.8. Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси Ох, проходит через точку М(-4; ) и имеет эксцентриситет е=3/4. Написать уравнение эллипса и найти фокальные радиус-вектор точки М.

Ответ:

8.9. Эллипс, главные оси которого совпадают с координатными осями, проходит через точки М₁(2; ) и М₂(0;2). Написать его уравнение, найти фокальные радиусы точки М₁ и расстояния этой точки до директрис.

Ответ: .

8.10. Эллипс, симметричный относительно осей координат, проходит через точки М(2 ) и А(6;0). Написать его уравнение, найти эксцентриситет и расстояния от точки М до фокусов.

Ответ:

8.11. Написать простейшее уравнение эллипса, у которого расстояния от одного из фокусов до концов большой оси равны 5 и 1.

Ответ: или

8.12. Установить, что каждое из следующих уравнений определяет эллипс, найти его центр С, полуоси, эксцентриситет и уравнения директрис:

Ответ: а) С(3;-1), а=3; b= , е=2/3, D₁: 2х+3=0; D₂: 2х-15=0;

в) С(1;-2), а=4; b= , е=1/2, D₁: у+10=0; D₂: у-6=0.

8.13.Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке F(-1;0), чем к прямой х=-4.

Ответ:

8.14.Написать уравнение кривой, по которой движется точка М, если сумма расстояний от нее до точек F₁(-1;-1) и F₂(1;1) остается постоянной и равной 2 .

8.15. Написать уравнение кривой, по которой движется точка М, если расстояние от нее до точки F(3;0) остается в два раза меньше расстояния до прямой х+у-1=0.

8.16. Построить эллипс , его директрисы и найти расстояния от точки эллипса с абсциссой х=-3 до правого фокуса и правой директрисы.

8.17. Построить гиперболу 16х 2 -9у 2 =144. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

8.18.Построить гиперболу х 2 -4у 2 =16 и ее асимптоты. Найти фокусы, эксцентриситет, угол между асимптотами.

Ответ:

8.19. Написать каноническое уравнение гиперболы, если: а) а=2, b=3; б) b=4, с=5; в) с=3, е=3/2; г) а=8, е=5/4; д) с=10 и уравнения асимптот ; е) е=3/2 и расстояние между директрисами равно 8/3.

Ответ: а) б) в) ; г)

д) е)

8.20. Гипербола симметрична относительно осей координат, проходит через точку М(6;-2 ) и имеет мнимую полуось b=2. Написать ее уравнение и найти расстояния от точки М до фокусов.

Ответ:

8.21.Убедившись, что точка М(-5;9/4) лежит на гиперболе , найти фокальные радиусы этой точки и ее расстояния до директрис.

8.22.Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса .

Ответ: .

8.23. Найти точки гиперболы , находящиеся на расстоянии 7 от фокуса F₁.

Ответ: (-6; ).

8.24.Построить гиперболу , ее директрисы и найти расстояния от точки гиперболы с абсциссой х=5 до левого фокуса и левой директрисы.

Ответ: Директриса х= 3,2, е=1,25, r=10,25, d=8,2.

8.25.Написать каноническое уравнение гиперболы, зная, что расстояния от одной из ее вершин до фокусов равны 9 и 1.

Ответ: или .

8.26. Найти точки пересечения асимптот гиперболы х 2 -3у 2 =12 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

Ответ: (0; 0) и (6; ).

8.27. Установить, что каждое из следующих уравнений определяет гиперболу, найти ее центр, полуоси, эксцентриситет, уравнения асимптот и директрис:

Ответ: а) С(2;-3), а=3, b=4, е=5/3, уравнения асимптот: 4х-3у-17=0 и 4х+3у+1=0; уравнения директрис: 5х-1=0 и 5х-19=0; б) С(-5;1), а=8, b=6, е=5/4, уравнения асимптот: 3х+4у+11=0 и 3х-4у+19=0; уравнения директрис: х=-11,4 и х=1,4; в) С(2;-1), а=4, b=3, е=5/4, уравнения асимптот: 4х+3у-5=0 и 4х-3у-11=0; уравнения директрис: у=-4,2 и у=2,2.

8.28. Построить следующие параболы и найти их параметры:

8.29. Построить параболы, заданные уравнениями: 1) у 2 =4х; 2) у 2 =-4х; 3) х 2 =4у; 4) х 2 =-4у, а также их фокусы и директрисы и написать уравнения директрис.

8.30. Составить уравнение геометрического места точек, одинаково удаленных от точки F(0;2) и от прямой у=4. Найти точки пересечения этой кривой с осями координат и построить ее.

Ответ:

8.31. Написать уравнение параболы с вершиной в начале координат, если известно, что:

а) парабола расположена в левой полуплоскости симметрично относительно оси Ох и р=1/2;

б) парабола расположена симметрично относительно оси Оу и проходит через точку М(4;-8);

в) фокус параболы находится в точке F(0;-3).

8.32. Написать уравнение параболы: 1) проходящей через точки (0;0) и (-1;2) и симметричной относительно оси Ох; 2) проходящей через точки (0;0) и (2;4) и симметричной относительно оси Оу.

Ответ: 1) 2) .

8.33.Установить, что каждое из следующих уравнений определяет параболу, найти координаты ее вершины А и величину параметра р:

8.34. Вычислить фокальный радиус точки М параболы у 2 =12х, если у(М)=6.

8.35. Зеркальная поверхность прожектора (рис.2) образована вращением параболы вокруг ее оси симметрии.

Рис.2

Диаметр зеркала 80 см, а глубина его 10 см. На каком расстоянии от вершины параболы нужно поместить источник света, если для отражения лучей параллельным пучком он должен быть в фокусе параболы?

8.36.Определить область расположения кривой . Построить кривую.