Написать уравнение эллипса зная его центр и концы двух сопряженных диаметров (2 видео)

Содержание

Написать уравнение эллипса зная его центр и концы двух сопряженных диаметров
Глава 22. Диаметры линий второго порядка
Эллипс
Определение эллипса.
Фокусы, эксценриситет и директрисы эллипса.
Уравнение касательной к эллипсу.
05.4. Задачи и размышления
Задачи и размышления
Уравнение кривой второго порядка
🎥 Видео

Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Написать уравнение эллипса зная его центр и концы двух сопряженных диаметров

Видео:ЭллипсСкачать

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

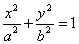
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

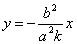
Если гипербола задана уравнением

, (2)

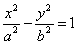
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

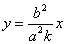
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

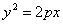
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

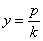
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

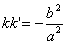
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

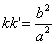
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Эллипс

Видео:11 класс, 52 урок, ЭллипсСкачать

Определение эллипса.

Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>+frac<y^><b^>=1label
$$
при условии (a geq b > 0).

Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).

Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.

Рис. 8.1. Эллипс

В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_), (M_) и (M_) (рис. 8.1). Следовательно, справедливо следующее утверждение.

Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.

Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^+y^=a^). При каждом (x) таком, что (|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Фокусами называются точки (F_) и (F_) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Отметим, что (varepsilon Утверждение 2.

Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_=|F_M|=a-varepsilon x, r_=|F_M|=a+varepsilon x.label
$$

Очевидно, что (r_^=(x-c)^+y^). Подставим сюда выражение для (y^), найденное из уравнения эллипса. Мы получим
$$
r_^=x^-2cx+c^+b^-frac<b^x^><a^>.nonumber
$$

Учитывая равенство eqref, это можно преобразовать к виду
$$
r_^=a^-2cx+frac<c^x^><a^>=(a-varepsilon x)^.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).

Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_+r_=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^+y^>=2a-sqrt<(x+c)^+y^>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=asqrt<(x+c)^+y^>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^x^+a^y^=a^b^), равносильному уравнению эллипса eqref.

Рис. 8.4. Фокусы и директрисы эллипса.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_(x_, y_)) — точка на эллипсе и (y_ neq 0). Через (M_) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ > 0) это график (f_(x)=bsqrt<1-x^/a^>), для (y_ Утверждение 5.

Касательная к эллипсу в точке (M_(x_, y_)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Рис. 8.5.

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

05.4. Задачи и размышления

Задачи и размышления

Знакомство со свойствами эллипса, гиперболы и параболы вызывает желание изучить способы построения этих кривых. Рассмотрим некоторые из таких способов.

1. Эллипс можно построить с помощью нити длиной 2а, закрепленной концами в фокусах (рис. 5.20). Очевидно, что длина нити останется неизменной, а фокусы фиксированы. Перемещая нить в натянутом состоянии, получим эллипс.

Рис. 5.20. Построение эллипса с помощью нити,
закрепленной в его фокусах.

Этот способ не всегда может быть удобен на практике. Дадим другой вариант построения эллипса, также вытекающий из его определения.

2. Пусть известно полуфокусное расстояние эллипса C и его большая полуось а.

Располагая фокусы F1 и F2 на расстоянии 2с, проводим дуги окружностей радиусами И поочередно из первого и второго фокусов, выбирая их так, чтобы

Точки пересечения окружностей будут лежать на эллипсе.

При этом допустимые значения и должны удовлетворять условиям:

Откуда следуют эти ограничения?

Меняя и В допустимых границах и строя соответствующие пары окружностей, в их пересечении будем получать точки, принадлежащие искомому эллипсу. Попарные значения и удобно выбрать, используя отрезок длиной 2а (рис. 5.21).

Рис. 5.21. Выбор допустимых значений модулей
фокальных радиусов.

Вершины эллипса, лежащие на малой оси, найдутся при пересечений дуг окружностей c радиусами , проведенных из фокусов и , как из центров.

Рис. 5.22. Построение эллипса по опорным точкам,
получаемым с помощью циркуля.

Для нахождения вершин эллипса, расположенных на большой оси, проводим дуги окружности радиуса a + c из фокусов F1 и F2, как из центров, до пересечения с этой осью.

Докажите, что полученная кривая – эллипс.

3. Рассмотрим еще один способ отыскания точек, принадлежащих эллипсу, с помощью построений, выполняемых линейкой. Построим прямоугольник АBСD, большая сторона которого AD равна 2а – длине большой оси эллипса, а длина меньшей стороны АВ равна 2b – его малой оси (рис. 5.23). Стороны АВ и ВС делим на одинаковое число равных частей. Точки деления соединяем с точками А и D. Выделенные на рисунке точки пересечения лежат на дуге эллипса.

Докажите этот факт.

Рис. 5.23. Построение эллипса по опорным точкам
с помощью линейки.

Подобным способом можно построить параболу (рис. 5.24).

Рис. 5.24. Построение параболы по опорным точкам
с помощью линейки.

Обоснуйте этот способ. Каким будет каноническое уравнение эллипса при известной длине отрезков AB и BC?

4. Рассмотрим один из возможных способов построения гиперболы. Будем считать известными расстояние 2с между фокусами F1 и F2 и разность модулей фокальных радиусов , где 2A – длина ее действительной оси.

Поместим в фокус F1 конец линейки (рис. 5.25), к другому концу которой в точке А прикреплен шнур, длина которого меньше длины линейки на 2а. Другой конец шнура закреплен в фокусе F2.

Рис. 5.25. Построение гиперболы с помощью натянутого шнура и линейки.

При вращении линейки вокруг фокуса F1 натянутый нитью острый конец карандаша (точка М) опишет некоторую кривую.

Для любой точки М на этой кривой будет справедливо:

Что соответствует свойствам гиперболической кривой. Мы получили правую ветвь гиперболы. Аналогично строится ее левая часть.

5. Придумайте новые способы построения эллипса, гиперболы, параболы и обоснуйте их.

Известные понятия диаметра окружности и ее хорды можно обобщить на эллипс, гиперболу и параболу.

Диаметром эллипса (гиперболы) называется любая прямая, проходящая через центр кривой. Диаметром параболы назовем любую прямую, параллельную ее оси, включая и саму ось.

Всякая прямая может пересекать коническое сечение не более чем в двух точках. Если точек пересечения две, то отрезок прямой с концами в точках пересечения называется хордой.

У рассматриваемых кривых обнаруживается одно неожиданное свойство: Середины параллельных хорд конических сечений лежат на их диаметре (рис. 5.26).

Рис. 5.26. Расположение середин параллельных хорд конических сечений.

Для доказательства этого свойства рассмотрим сначала эллипс и гиперболу. Оно очевидно, когда хорды перпендикулярны вертикальной оси симметрии этих кривых. Возможны другие случаи. Пусть семейство параллельных хорд задается уравнением:

Меняя b, мы будем получать параллельные прямые. Уравнения эллипса и гиперболы можно объединить следующей записью:

Координаты концов хорд должны удовлетворять следующей системе уравнений:

Подставляя из второго уравнения этой системы выражение для координаты у в первое, получим:

По теореме Виета легко найти

Полусумма решений и будет являться абсциссой хc середины хорды:

Используя уравнение хорды, находим ординату ее середины:

Таким образом, середины параллельных хорд лежат на прямой

Проходящей через центр эллипса или гиперболы, то есть являющейся диаметром кривой. Угловой коэффициент этого диаметра

Он называется сопряженным по отношению к диаметру , параллельному хордам.

Интересно, что свойство сопряженности диаметров взаимно. Так, угловой коэффициент диаметра, сопряженного диаметру

Рассмотрим теперь параллельные хорды параболы

При разных значениях b. Их концы должны удовлетворять системе:

Выполняем очевидные преобразования аналогично предыдущему:

Это означает, что середина хорды имеет ординату

Таким образом, геометрическое место середин хорд параболы – прямая, параллельная оси 0х, то есть диаметр параболы.

6. Дано семейство параллельных прямых,

На которых располагаются параллельные хорды эллипсов:

Всегда ли они будут иметь один и тот же сопряженный диаметр?

7. Дана парабола х = 2у2, ее диаметр и семейство параллельных хорд, образующих с осью 0х угол j= 0,2. Найти длину хорды, пересекающей ось абсцисс в точке х = 2.

8. Хорда эллипса

Наклонена под углом j к оси 0х и имеет длину l. Найдите координаты ее концов. Исследуйте решение.

Вписаны треугольники АВL и СDL так, что стороны АВ=l и СD=m расположены параллельно, а медианы КL и МL лежат на одной прямой. Найти длины медиан. Доказать, что прямая МL пройдет через начало координат. Исследовать решение задачи в зависимости от входящих в него параметров.

10. Дан параллелограмм со сторонами a и b, угол между которыми j. Построить несколько эллипсов, которые могут быть описаны около этого параллелограмма, и найти их уравнения.

11. Доказать, что сумма квадратов двух сопряженных полудиаметров эллипса равна сумме квадратов его полуосей.

12. Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, равна площади прямоугольника, построенного на полуосях эллипса.

13. По изображению эллипса найти с помощью циркуля и линейки его центр.

14. Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра, параллельны паре его сопряженных диаметров.

15. Доказать, что отрезки, отсекаемые директрисами на асимптотах, считая от центра гиперболы, равны действительной полуоси. Пользуясь этим свойством, построить директрисы гиперболы.

Рассмотрим параметрические уравнения эллипса. В связи с этим обратимся к задаче.

Пусть точка М делит отрезок АВ на части a и b. Его концы скользят по сторонам прямого угла. Какую траекторию опишет при этом точка М?

Для решения задачи введем прямоугольную декартовую систему координат, расположив ее начало в вершине угла, а оси координат – по направлению сторон прямого угла (рис.5.27). Пусть точка М имеет координаты х и у, а угол , который образован отрезком AB с отрицательной ориентацией оси Ох, равен t радиан.

Рис. 5.27. Вывод параметрических уравнений эллипса

При перемещении концов отрезка А и В по координатным осям (во всех четырех координатных углах) точка М(х, у) опишет кривую, параметрические уравнения которой легко находится:

Этой кривой является эллипс, в чем можно убедиться, исключая параметр t. Действительно,

16. Найдите параметрические уравнения гиперболы и параболы.

17. Точка М, брошенная под углом к горизонту с начальной скоростью (рис.5.28а), если пренебречь сопротивлением воздуха, движется согласно уравнениям:

Где g — ускорение силы тяжести. На возвышенности, образующей с горизонтом угол , располагается перпендикулярно ей стержень высоты h.

Расстояние от подножья возвышенности до точки М равно l, а до основания стержня – d.

При каких углах точка М сможет перелететь через стержень?

Исследуйте допустимые углы перелета точки М через квадрат, установленный на возвышении вместо стержня (рис.5.28б).

Рис. 5.28. Траектория точки М, преодолевающей препятствия.

18. На рис.5.29 указаны проекции стойки. Ее основание ограничено дугами эллипса. Для крепления стойки к поверхности предполагается просверлить отверстия в тех ее точках, которые соответствуют фокусам эллипса. Используя чертеж детали, опишите аналитически этот эллипс, вычислите его фокусы, укажите на чертеже точки для сверления отверстий и вычислите расстояние от этих точек до наиболее удаленных точек стойки.

19. Верхний слой воды в наклоненном цилиндрическом стакане имеет форму эллипса (рис.5.30). Докажите этот факт и найдите полуоси эллипса, если радиус цилиндра R, а угол наклона .

Рис. 5.30. Верхний слой воды в наклоненном стакане.

20. Найдите траекторию точки, которая во все время движения остается вдвое ближе от заданной прямой, чем от заданной точки.

21. Найдите траекторию точки, для которой во все время движения произведение расстояний до двух данных пересекающихся прямых есть величина постоянная.

На основании первого закона Кеплера Земля движется вокруг Солнца по эллиптической орбите, в одном из фокусов которой расположено наше светило. Найдем скорость Земли в точке наибольшего удаления планеты от Солнца, если эксцентриситет орбиты e=0,0167; большая полуось a=149504000 км; масса Солнца mc=1,97×1030 кг (рис. 5.31).

Рис. 5.31. Орбита вращения Земли вокруг Солнца

Движение Земли в поле гравитации подчиняется закону сохранения энергии, согласно которому во всякой точке орбиты ее полная механическая энергия остается постоянной. Пусть и – радиус-векторы, определяющие, соответственно, наиболее и наименее удаленное положение Земли на орбите вокруг Солнца. Если

Есть кинетическая энергия Земли в точках A и B орбиты соответственно, где m3 – ее масса, и равенства

;

Характеризуют ее потенциальную энергию в гравитационном поле Солнца в этих точках, где G=6,67×10-11 м3/кгс2 – гравитационная постоянная, то

;

Это уравнение содержит две неизвестные: и . Чтобы преодолеть возникшую трудность, воспользуемся вторым законом Кеплера, согласно которому, радиус-вектор планеты за одинаковые промежутки времени зачерчивает одинаковые площади. Примем упрощенную гипотезу: за малые промежутки времени траекторию Земли можно считать прямолинейной. Тогда площади соответствующих секторов выразятся приближенно следующим образом:

;

И мы придем к соотношению:

Из которого находим связь между скоростями и :

Получаем следующее уравнение относительно неизвестной :

М/с.

Вот с какой скоростью мчится наша Земля в космическом пространстве. А ведь эта скорость минимальная. В точке В она будет еще выше.

22. Найдите наименьшую и наибольшую скорость Марса на орбите вокруг Солнца, используя соответствующие справочные данные.

Третий закон Кеплера гласит: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит:

23. Используя этот результат, найдите большую полуось орбиты первого искусственного спутника Земли, который был запущен в 1957 году в СССР и имел период обращения 1 час 55 минут по эллиптической орбите, если период обращения Луны вокруг Земли равен 655,2 ч., большая полуось лунной орбиты составляет 382000 км и наименьшее удаление искусственного спутника от центра Земли – 6603 км. Радиус Земли принять равным 6378 км.

Интересно отметить, что скорость, которую необходимо сообщить искусственному спутнику вблизи поверхности Земли в горизонтальном направлении, чтобы он начал двигаться в качестве спутника по круговой орбите радиуса R (рис.5.32), определяется формулой:

Принимая g=9,81 м/с2, , получим . Это значение скорости называется первой (1) космической скоростью.

Если скорость V1 будет стремиться к значению

Равного для Земли, , то орбита искусственного спутника станет эллиптической и, достигнув, величины V2, второй космической скорости – станет параболической.

При скорости, большей второй космической, спутник будет двигаться по гиперболе.

В последних двух случаях, спутник навсегда покинет Землю и удалится в межпланетное пространство.

Рис. 5.32. Зависимость формы орбиты искусственного спутника Земли от начальной скорости.

24. Между Землей и Луной пролетает космический аппарат так, что расстояния от него до поверхности Земли и до поверхности Луны постоянно остаются равными между собой. Составьте математическую модель, описывающую это движение. В каких условиях она допускает упрощения?

25. На самолетах и кораблях во время второй мировой войны действовала навигационная система, использовавшая разницу времени между моментами приема радиосигналов от двух пар станций, которые испускали их одновременно. Составьте математическую модель этой навигационной системы и оцените ее достоинства и недостатки.

В прожекторах, фарах автомобилей используется параболоид вращения, который получается при вращении параболы вокруг собственной оси: лучи, выходящие из источника света, помещенного в фокус, не рассеиваются, а, отразившись от стенок параболоида, идут параллельно этой оси. Используется и обратный эффект. «Тарелка» – так называется параболическая антенна для спутниковой связи, собирает в одну точку телевизионные сигналы, идущие из космоса. Фокальные свойства кривых второго порядка давали повод для мифотворчества. Очевидно, что в повести «Гиперболоид инженера Гарина» А. Толстой имел в виду все-таки параболоид.

Еще раньше зародилась легенда об Архимеде из Сиракуз, который сжег флот римлян, обороняя свой город с помощью параболических зеркал.

26. Составьте технический проект такой «пушки», которая могла бы поражать противника на расстоянии 50-500 м. Попробуйте оценить ее поражающую мощь.

Вернемся к задаче Паппа, которая была поставлена в начале главы, как к одной из первых решенных Р. Декартом аналитическим методом. Дадим ее общую формулировку.

Даны 2n прямых, лежащих в одной плоскости. Найти геометрическое место точек в этой плоскости, таких, что произведение расстояний от каждой точки этого множества до первых n прямых d1×D2. . ×Dn и произведение расстояний от этих же точек до следующих n прямых dn+1×Dn+1×. ×D2n находились бы для всех точек в одном и том же постоянном отношении L:

Попытка решить ее для n=3 (рис. 5.33) была предпринята нами ранее. Рассмотрим общий случай. Введем систему координат, выбирая ее начало в произвольной точке плоскости и опишем положение заданных прямых соответствующими нормальными уравнениями:

Рис. 5.33. Задача Паппа при n=3.

Пусть – произвольная точка искомого геометрического места точек. Найдем расстояния от нее до данных прямых:

Это и есть уравнение искомой кривой относительно координат x’ и у’ ее точек. Оно будет иметь степень n, в частном случае, например, для четырех прямых 2n=4; n=2 мы получим уравнение второй степени. Такое уравнение, как это уже отмечалось на стр.180, определяет одно из конических сечений. Это весьма неожиданный результат.

27. Каковы возможные обобщения задачи Паппа?

Видео:Видеоурок "Гипербола"Скачать

Уравнение кривой второго порядка

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Диаметры кривой. Главные оси. Асимптоты. Уравнение кривой, отнесенной к сопряженным направлениям; уравнение кривой, отнесенной к асимптотам.

Если в кривой второго порядка провести все хорды одного и того же направления, то геометрическое место середин этих хорд представит некоторую прямую, которую называют диаметром, сопряженным данным хордам. Уравнение диаметра:

где есть угловой коэффициент сопряженных хорд. Меняя , т.е. меняя направление хорд, получим бесчисленное множество диаметров; все они проходят через центр кривой. У параболы все диаметры параллельны между собой.

Направление хорд и направление сопряженного им диаметра называются сопряженными направлениями относительно данной кривой. Зависимость между двумя сопряженными направлениями следующая:

Сопряженными диаметрами называются такие два диаметра, из которых каждый делит пополам хорды, параллельные другому. У параболы сопряженных диаметров нет, так как все диаметры имеют одно и тоже направление.

Главными осями кривой называются диаметры, перпендикулярные к сопряженным хордам; их направления называются главными направлениями.

В случае прямоугольной системы координат главные направления определяются из уравнения:

где – угол между одним из главных направлений и направлением оси .

В случае косоугольной системы координат имеем:

Всякая кривая второго порядка имеет два главных направления, за исключением окружности, для которой главные направления неопределенные.

Угловой коэффициент определяется для всех диаметров параболы по формуле:

если для старших коэффициентов параболы введены обозначения:

Главная ось параболы как один из ее диаметров имеет это же направление и в случае прямоугольных координат она изображается уравнением

Второе главное направление параболы перпендикулярно к ее диаметрам, но второй главной оси у параболы нет. Если отнести кривую у двум сопряженным направлениям, т.е. выбрать за оси координат прямые, имеющие сопряженные направления относительно этой кривой, то в уравнение кривой не войдет член с произведением координат (). У параболы кроме того, исчезнет ещё один из старших членов ().

Если центральную кривую отнести к двум сопряженным диаметрам (или к главным осям), то уравнение ее примет вид:

Простейшее уравнение параболы мы получим, поместив начало координат в вершину, т.е. в точку пересечения параболы с главной осью (), выбрав главную ось за ось абсцисс (, и ) и касательную в вершине (она перпендикулярна к оси) за ось ординат:

При таком же выборе осей координат центральная кривая изобразится уравнением

Асимптоты кривой можно рассматривать как те ее диаметры, которые сами себе сопряжены. Угловые коэффициенты асимптот определяются из уравнения

Асимптоты могут быть только у центральных кривых: гипербола имеет две действительные асимптоты, эллипс – две мнимые; в случае пересекающихся прямых асимптоты совпадают с этими прямыми.

Если принять асимптоты гиперболы за оси координат, то уравнение этой гиперболы примет вид:

587. Найти два сопряженных диаметра кривой , из которых один проходит через начало координат.

Решение . Данная кривая центральная, потому что . Уравнение всякого ее диаметра будет где — угловой коэффициент сопряженного диаметра. Так как искомый диаметр проходит через начало координат, то свободный член его уравнения должен равняться нулю, т.е. откуда . Вставив это значение параметра в общее уравнение диаметра и преобразовав его, получим: . Это уравнение одного из искомых диаметров; его угловой коэффициент ; следовательно, уравнение сопряженного диаметра будет:

588. Через точку (1;-2) проведен диаметр кривой . Найти уравнение этого диаметра и диаметра ему сопряженного.

589. Дана кривая . Найти ее диаметр, параллельный оси абсцисс, и диаметр, ему сопряженный.

590. Найти два сопряженных диаметра кривой , из которых один параллелен оси ординат.

591. Дана кривая и один из ее диаметров . Найти диаметр, ему сопряженный.

592. Составить уравнение диаметра кривой , параллельного прямой .

593. Определить диаметр кривой , образующий угол в с осью абсцисс. Угол .

594. Дана кривая: . Найти геометрическое место середин ее хорд: 1) параллельных оси ; 2) параллельных оси ; 3) параллельных прямой .

595. Найти диаметр кривой , проходжящей через середину хорды, отсекаемой этой кривой на прямой .

596. Найти середину хорды, отсекаемой кривой на прямой .

597. Найти такие сопряженные диаметры кривой , которые образуют между собой угол в . Угол .

598. Найти зависимость между угловыми коэффициентами прямых, имеющих сопряженные направления относительно:

1) эллипса ; 2) гиперболы .

599. Через точку (1;-3) провести хорду эллипса , сопряженную диаметру .

600. Найти направления и длину двух сопряженных диаметров эллипса , из которых один проходит через точку (2;3).

601. Найти угол между двумя сопряженными диаметрами эллипса , из которых один образует угол в с большой осью.

602. Определить длину тех сопряженных диаметров эллипса , которые образуют между собой угол .

Указание . В этой задаче удобно воспользоваться теоремами Аполлония: и , где и – полуоси эллипса; и — сопряженные полудиаметры его; – угол между этими сопряженными диаметрами.

603. Даны размеры двух сопряженных диаметров эллипса и и угол между ними . Вычислить длину его осей.

604. Определить угол между двумя сопряженными диаметрами гиперболы , зная, что действительный из этих диаметров втрое больше действительной оси.

605. Найти уравнения двух сопряженных диаметров гиперболы , угол между которыми равняется .

606. Дана парабола: . Написать уравнение диаметра этой параболы:

1) проходящего через начало координат;

2) сопряженного хордам, параллельным оси ;

3) сопряженного хордам, параллельным оси ;

4) образующего угол с сопряженными хордами;

5) перпендикулярного к сопряженным хордам.

Во всех случаях угол

607. Найти диаметр параболы , сопряженный тем хордам, которые наклонены под углом в к оси параболы.

608. Написать уравнение диаметра параболы , сопряженного с прямой .

609. Найти главные оси кривых:

Во всех случаях угол

610. Каковы будут главные оси распавшейся центральной кривой?

611. Найти ось параболы .

Решение . Все диаметры данной параболы имеют угловой коэффициент . Ось параболы есть диаметр, сопряженный перпендикулярным хордам, т.е. хордам с угловым коэффициентом (система координат предполагается прямоугольной). Уравнение всякого диаметра этой параболы будет при мы получим уравнение оси: .

612. Найти ось симметрии и вершину каждой из следующих парабол:

Во всех случаях угол

Указание . Вершина параболы находится как точка пересечение параболы с ее осью.

613. Найти общий диаметр двух кривых:

614. Составить уравнение кривой второго порядка, проходящей через начало координат, если известны две пары сопряженных ее диаметров:

Решение . Угловые коэффициенты сопряженных диаметров удовлетворяют уравнению: . Угловые коэффициенты данных диаметров: и , , ; вставляя эти значения в указанное уравнение, получим:

Координаты центра искомой кривой мы можем определить, решая совместно уравнения двух диаметров: , . Эти координаты должны удовлетворять уравнениям: и которые данном случае перепишутся так: и ; вставим вместо : и вычисленные их значения и тогда получим: и . Кроме того, кривая проходит через начало координат; значит, , и уравнение кривой будет:

615. Две пары прямых:

служат сопряженными диаметрами кривой второго порядка. Составить уравнение этой кривой, зная, что она проходит через точку (1;1).

616. Выяснить особенности в выборе осей координат, если кривые даны следующими уравнениями:

617. Относительно некоторой прямоугольной системы координат кривая дана уравнением: . Преобразовать это уравнение, приняв за оси координат главные оси кривой.

618. Отнести к главным осям кривые, данные относительно прямоугольной системы координат уравнениями:

619. Уравнение кривой, отнесенной к двум сопряженным диаметрам, составляющим угол , имеет вид: . Найти уравнение той же кривой относительно ее главных осей.

620. Отнести к главным осям кривые:

621. Выяснить особенности в выборе осей координат, если параболы даны следующими уравнениями:

622. привести к простейшему виду уравнение параболы ; .

623. Привести к простейшему виду уравнения следующих парабол:

624. Отнести к вершине следующие центральные кривые:

Во всех случаях .

625. Найти асимптоты следующих гипербол:

626. Доказать, что все кривые, уравнения которых отличаются друг от друга только свободными членами, имеют общие асимптоты. Найти, например, асимптоты кривых при различных значениях параметра λ.

627. Доказать, что если две кривые имеют общие асимптоты, то все члены их уравнений, кроме свободных членов, имеют пропорциональные коэффициенты.

628. Составить общее уравнение для всех кривых. Имеющих прямые и своими асимптотами.

629. кривая второго порядка проходит через точку (1;-1) и имеет своими асимптотами две прямые: и . Составить уравнение этой кривой.

630. Составить уравнение кривой, касающейся прямой и имеющей прямые и своими асимптотами.

630*. Какому условию удовлетворяют коэффициенты общего уравнения гиперболы, если гипербола равносторонняя?

631. Какой вид имеет уравнение гиперболы, если одна из осей координат или обе оси параллельны асимптотам?

632. Составить уравнение гиперболы, проходящей через точки (2;1), (-1;-2) и (), при условии, что одна из ее асимптот совпадает с осью абсцисс.

633. Уравнение гиперболы, отнесенной к главным осям, имеет вид: . Преобразовать это уравнение, приняв асимптоты гиперболы за новые оси координат.

634. Отнести гиперболу к ее асимптотам.

635. Как преобразуется уравнение гиперболы , если за оси координат принять ее асимптоты? Угол .

636. Сколько членов второй степени и какие именно могут войти в уравнение: 1) эллипса4 2) гиперболы; 3) параболы?

Преобразование уравнения кривой второго порядка с помощью инвариантов.

Если одна и та же кривая второго порядка, отнесенная к двум различным произвольно выбранным системам координат с координатными углами и , изображается уравнениями:

то имеют место следующие равенства:

т.е. существуют выражения, составленные из коэффициентов уравнения кривой и соответствующего координатного угла, которые не меняют своей величины ни при каком преобразовании декартовых координат. Такие выражения называются инвариантами кривой второго порядка. Мы можем пользоваться тремя вышеприведенными инвариантами:

для упрощения уравнений кривой второго порядка, если только уравнение кривой после преобразования содержит не более трех коэффициентов.

637. Пользуясь инвариантами, отнести к главным осям кривую , зная что .

Решение . Искомое уравнение имеет следующий вид:

Для прямоугольных систем координат инварианты упрощаются, так как и , и мы будем иметь: ; . Найдем числовое значение этих инвариантов, исходя из данного уравнения:

Составим теперь выражения этих же инвариантов через коэффициенты преобразованного уравнения: . Так как инварианты не меняют своей величины при преобразовании координат, то мы можем приравнять между собой найденные для них выражения, содержащие коэффициенты первоначального и преобразованного уравнения;. Из этой системы уравнений мы определяем неизвестные коэффициенты преобразованного уравнения: ;, и искомое уравнение будет . Таким образом, пользуясь инвариантами, можно привести уравнение кривой к простейшему виду, не отыскивая ее центра, осей и не составляя формул преобразования координат.

638. Пользуясь инвариантами, привести к простейшему виду уравнения следующих кривых:

при условии, что все они отнесены к прямоугольной системе координат.

639. Пользуясь инвариантами, упростить уравнения следующих кривых:

Во всех случаях .

640. Упростить уравнения следующих кривых:

640*. Отнести к главным осям кривую , если известно, что .

641. Отнести гиперболу к ее асимптотам, пользуясь инвариантами. Угол .

Решение . Уравнение кривой, отнесенной к асимптотам, имеет вид:

Нам надо найти два неизвестных коэффициента , и новый координатный угол , т.е. угол между асимптотами. Найдем числовую величину инвариантов, пользуясь данным уравнением, при , : . Выражения этих инвариантов в новых коэффициентах будут:

Для определения трех величин , и имеем три уравнения:

Решив их, получим: , ; и ; искомое уравнение будет: . Выбираем направление осей так, чтобы гипербола была расположена в нормальном угле и вертикальном к нему угле; тогда после упрощений получим: .

642. Отнести к асимптотам гиперболы, данные относительно прямоугольной системы координат уравнениями:

643. Относительно некоторой прямоугольной системы координат кривая изображается уравнением . Составить уравнение этой же кривой относительно ее вершины.

Указание . Отнести кривую к вершине – значит принять одну из осей кривой за ось абсцисс, перенести начало координат в вершину и принять касательную в вершине за ось ординат.