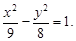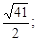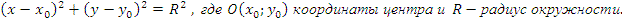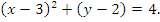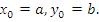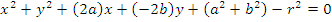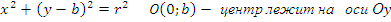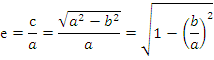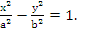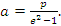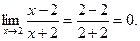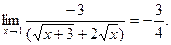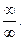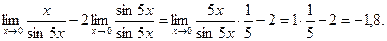Две гиперболы называются сопряженными (рис. 52), если они имеют общий центр О и общие оси, но действительная ось одной из них является мнимой осью другой.
На рис. 52 


есть уравнение одной из сопряженных гипербол, то другая представляется уравнением
Сопряженные гиперболы имеют общие асимптоты 
© 2022 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
Видео:Гипербола (часть 7). Директрисы гиперболы. Высшая математика.Скачать

Кривые второго порядка
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных, называемых фокусами, есть величина постоянная, равная 2a, и большая чем расстояние между фокусами, равное 2c (рисунок 6).
 |
| Рисунок 6 |
Простейшее каноническое уравнение эллипса получается в системе координат, в которой за ось абсцисс выбрана прямая, соединяющая фокусы, начало координат 0 − середина отрезка, концами которого служат фокусы, ось ординат – прямая, проходящая перпендикулярно оси ОX через точку 0. Тогда уравнение эллипса примет следую-
щий вид:
где
При таком выборе системы координат оси координат совпадают с осями симметрии эллипса, а начало координат − с центром симметрии. Точки А1(a; 0), А2(–a; 0), В1(0; b), В2(0; –b) называются вершинами эллипса. Отрезки, заключенные между вершинами, называются осями эллипса: большая (фокальная) ось А1А2 = 2a, малая ось В1В2 = 2b. Параметры a и b уравнения равны полуосям эллипса. Эксцентриситетом (e) эллипса называется отношение расстояния (2c) между фокусами к большей оси (2a), т. е. 
Пример 11. Составить каноническое уравнение эллипса, зная, что малая полуось равна 3 и эксцентриситет
Уравнение будем искать в виде
Из условия b = 3. Так как с одной стороны 




Ответ:
Тест 22. Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид:
1)
2)
3)
Тест 23. Дано уравнение эллипса
Вычислить длину осей, фокусное расстояние, эксцентриситет:
1) 16; 9; 25;
2) 8; 6; 2
Пример 12. Дан эллипс 
Уравнения директрис следующие: 
b 2 = 20. Следовательно, a = 6, 

Уравнение эллипса, центр которого находится в точке (х0; у0), а оси симметрии параллельны осям координат, имеет вид
Тест 24. Центр эллипса 
Гиперболой называется множество точек плоскости, модуль разности от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a, и меньшая чем расстояние между фокусами, равное 2c (рисунок 7).
 |
Простейшее каноническое уравнение гиперболы имеет вид

Прямая, соединяющая фокусы F1, F2 гиперболы, служит осью абсцисс, начало координат находится в середине между фокусами; при этом оси координат совпадают с осями симметрии гиперболы, начало координат – с ее центром симметрии (оси и центр гиперболы).
Гипербола имеет две действительные вершины А1(a; 0), А2(–a; 0) на фокальной оси; отрезок А1А2 = 2a называется действительной осью гиперболы, отрезок В1В2 = 2b – мнимой осью гиперболы. Таким образом, параметры a и b в уравнении гиперболы равны длинам действительной и мнимой полуосей соответственно.
Если a = b, то гипербола называется равносторонней.
Если мнимая ось гиперболы имеет длину 2a и направление по оси x, а действительная ось, длиной 2b, совпадает с осью y, то уравнение такой гиперболы имеет следующий вид:

где
Гиперболы (1) и (2) называются сопряженными гиперболами.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к действительной оси: e = 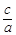


Если точка, двигаясь по гиперболе, неограниченно удаляется, то расстояние ее от одной из асимптот стремится к нулю. Асимптоты являются диагоналями прямоугольника со сторонами 2a, 2b (рисунок 7).
Пример 13.Составить уравнение гиперболы, оси которой совпадают с осями координат, зная, что:
1. Расстояние между вершинами равно 8, а расстояние между фокусами – 10.
2. Действительная ось равна 6, гипербола проходит через точку
(9; –4).
1. Уравнение гиперболы имеет вид
Так как расстояние между вершинами равно 8, то 2a = 8 или a = 4. Учитывая, что расстояние между фокусами равно 10, имеем 2c = 10, откуда c = 5. Найдем b 2 из соотношения b 2 = c 2 – а 2 , т. е. b 2 = 5 2 – 4 2 =
= 25 – 16 = 9.
Ответ:
2. Так как действительная ось равна 6, то 2a = 6 или a =3. Поэтому уравнение гиперболы принимает вид 




Ответ:
Тест 25. Уравнение гиперболы, действительная ось которой равна 10 и лежит на оси ОX, а мнимая ось равна 16 и лежит на оси ОY, имеет вид:
1)
2)
3)
Тест 26. Дано уравнение гиперболы 
1) 10; 16; 2
2) 4; 5;
3) 5; 4;
Пример 14. Дана гипербола 
Из уравнения а 2 = 16, b 2 = 25. Откуда a =4, b =5. Найдем 


Уравнения асимптот 
Ответ: x = 
Тест 27. Указать, принадлежит ли точка (0; 2) гиперболе 
Уравнение гиперболы, центр которой находится в точке (х0; у0), действительная ось совпадает с осью ОX, мнимая – с осью ОY, имеет вид
Тест 28. Центр гиперболы 
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Парабола
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой параболы (рисунок 8).
 |
| Рисунок 8 |
Если за ось абсцисс принять перпендикулярную прямую, проведенную из фокуса к директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид
где р – параметр параболы, расстояние от фокуса параболы до ее директрисы.
Парабола имеет одну ось симметрии, которая совпадает при таком выборе системы координат с осью X. Единственная вершина параболы совпадает с началом координат и является единственной точкой пересечения параболы с осями.
Пример 15. Составить уравнение параболы, зная, что фокусы имеют координаты (0; 5), ось ординат служит осью симметрии, а вершина находится в начале координат.
Так как осью симметрии является ось ОY, то уравнение будет иметь вид х 2 = 2ру, так как фокус в общем случае имеет координаты 

Тест 29. В уравнении параболы у 2 = 3х значение параметра p равно:
2) 
Тест 30. Среди уравнений второго порядка указать уравнение гиперболы:
1)
2)
3)
Если вершина параболы находится в точке (x0; y0), то ее каноническое уравнение примет следующий вид:
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Векторная алгебра
При изучении различных разделов экономики, механики, физики, других учебных дисциплин приходится иметь дело с величинами, для характеризации которых в выбранной системе единиц достаточно указать их численные значения. Эти величины называются скалярными. К числу скалярных величин можно отнести длину, площадь, объем, массу, температуру и т. п. Встречаются, тем не менее, такие величины, для определения которых необходимо знать их направления в пространстве. Указанные величины будем называть векторными. Примерами векторных величин являются сила, скорость, ускорение.
Геометрические векторные величины изображаются с помощью направленных отрезков.
Связанным вектором (или направленным отрезком) называется любой отрезок прямой, если только указано, какая из двух ограничивающих его точек является начальной, какая – конечной. Если точка А – начало отрезка, а точка В – его конец, то связанный вектор будем обозначать 
Длиной 
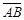

Связанные векторы 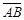


Два ненулевых связанных вектора 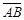

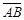

Свободным вектором а (или просто вектором) назовем множество равных между собой связанных векторов. При дальнейшем из контекста будет ясно, какой вектор имеется в виду (связанный или свободный). Для задания вектора достаточно указать какой-либо один вектор из всего множества <AB, CD, MN, ¼> равных связанных векторов, например, 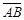
Рассмотренные понятия (длина, направление и т. п.), которые введены для связанных векторов, имеют аналоги также и для свободных. Часто векторы обозначают одной жирной строчной буквой: 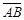
Линейные операции над векторами
Определим для свободных векторов операции их сложения, вычитания, умножения вектора на действительное число.
Суммой двух векторов a и b по правилу треугольника называется такой третий вектор с, что начало его совпадает с началом вектора а, а конец – с концом вектора b.
Иногда вместо с = а+bпишут 
… + аn конечного числа векторов называется такой вектор а, который замыкает ломаную линию, построенную из данных векторов а1, а2,…, аn таким образом, что начало каждого последующего вектора совпадает с концом предыдущего. Указанный вектор а направлен из начала первого вектора суммы в конец последнего (правило многоугольника) (рисунок 10).
c = a + b
На рисунке 11 изображена сумма а = а1 + а2 + а3 + а4 + а5 векторов а1, а2, а3, а4, а5.
Произведением вектора а на число a называется вектор b = a а, длина которого равна 
a 0 будем обозначать единичный вектор, имеющий направление вектора а.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка
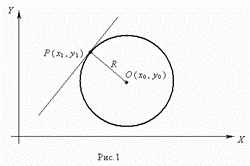
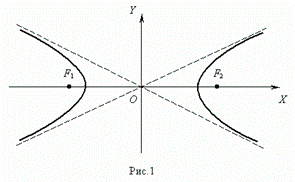
Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.
Уравнение окружности имеет вид
Например:
Переход от последнего уравнения к общему виду. Для удобства заменим
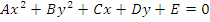

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: 
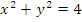
Пусть Р ( х1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:
Условие касания прямой y = m x + k и окружности х 2 + у 2 = R 2 :
ПРИМЕР 1. 
Решение: Разделив уравнение на 2 и сгруппировав члены уравнения, получим х 2 — 4х +у 2 + 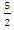
(х 2 — 
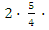


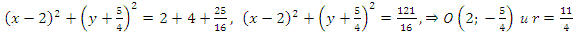
Ответ: 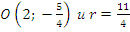
Эллипсом ( рис. ) называется множество точек плоскости, сумма расстояний которых до двух данных точек F1 и F2 , называемых фокусами эллипса, есть величина постоянная, равная 2a.

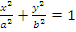
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ , при a CD = 2 b – малой осью эллипса.
При изменении e от 0 до 1, эллипс будет из окружности, постепенно, сжимаясь,
трансформироваться во всё более и более вытянутую кривую пока не перейдет в
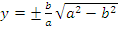
Аналогично 
Достаточно рассмотреть его часть в 1 четверти и тогда y > 0 и х > 0, можно построить график функций
· Отрезок прямой соединяющий две точки эллипса называется хордой.
Оси симметрии – просто Ось эллипса.
Точка пересечения – центр.
· Точки в которых эллипс пересекает оси называются вершинами.
· Осями называют также отрезки B1B = 2b, A1A = 2a
Фокальная ось – ось на которой расположены фокусы.
Если 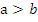
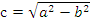
Если 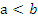
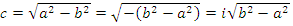
величина. Фокусы будут на оси ординат, фокальной осью будет 2b.
Пусть Р ( х1 , у 1 ) – точка эллипса, тогда уравнение касательнойк эллипсув данной
точке имеет вид: 
Условие касания прямой y = m x + k и эллипса х 2 / a 2 + у 2 / b 2 = 1 :
ПРИМЕР 3.Найти каноническое уравнение эллипса, зная его большую полуось а =5 и эксцентриситет е = 0,6..
Решение: Зная, что e 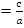


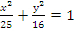
Ответ: 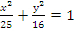
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек F1 и F2 , называемых фокусами гиперболы, есть величина постоянная, равная 2a.
Каноническое уравнение гиперболы.
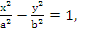
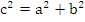
Гипербола 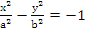
Числа a и b называются соответственно вещественной и мнимыми полуосями гиперболы.
· Ось гиперболы – прямая соединяющая её фокусы.
· Расстояние от начала координат до одного из фокусов гиперболы, называют фокусами расстояний гиперболы.
· Расстояние от начала координат до одной из вершин гиперболы называют большой или вещественной полуосью гиперболы a,
· Расстояние от вершины гиперболы до асимптоты в доле направления параллельное оси ординат называется малой или мнимой полуосью гиперболы b,
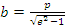
· y = 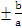
· Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом 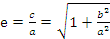

· Расстояние от фокуса до гиперболы вдоль прямой параллельной Оси ординат называется фокальным параметром р, 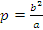
· Парацентрическое расстояние (r.p.) – расстояние от фокуса до ближайшей вершины гиперболы 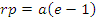
· Предельным параметром называют расстояние от фокуса до одной из асимптот гиперболы. Предельный параметр равен малой полуоси гиперболы.
Пусть Р ( х1 , у 1 ) – точка гиперболы, тогда уравнение касательнойк гиперболев данной
точке имеет вид: 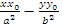
Условие касания прямой y = m x + k и гиперболы х 2 / a 2 — у 2 / b 2 = 1 :
ПРИМЕР 1.Написать каноническое уравнение гиперболы, проходящей через точку М( 
Решение: По условию 2с = 20, с =10. Запишем каноническое уравнение гиперболы 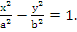


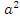
Решим систему уравнений 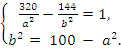
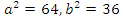
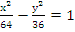
Ответ:
ПРИМЕР 2.Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен 13/12.
Решение: По условию 2с=26, с=13 и e =c/a=13/12. Следовательно, большая полуось гиперболы a = 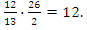

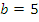
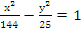
Ответ: 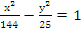
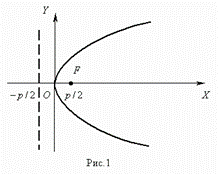
Каноническое уравнение параболы( рис. ) :
Число р — параметр параболы. Начало координат О(0;0) – вершина параболы, а ось ОХ является осью симметрии параболы. Точка F(p/2; 0) – фокус параболы, х = -р/2 директриса параболы.
Пусть Р ( х1 , у 1 ) – точка параболы, тогда уравнение касательной к параболев данной точке имеет вид: у 1 y = p ( x + х1) .
Условие касания прямой y = m x + k и параболы y 2 = 2 p x: 2 m k = p .
ПРИМЕР 4.Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси Ох. равна 16, а расстояние этой хорды от вершины равно 6.
Решение: Так как известны длина хорды и расстояние ее от вершины, то, следовательно, известны координаты конца этой хорды – точки М, лежащей на параболе. Уравнение параболы имеет вид y 2 = 2px; полагая в нем х = 6 и у = 8, находим 8 2 =2р
2 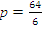
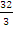
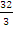
Ответ: y 2 = 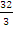
Число А называется пределом функции f(x) при 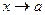
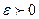
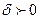
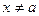
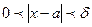


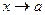
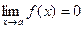
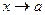
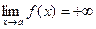
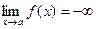
Свойства б/м и б/б функций:
· Если f(x) и g(x) – б/м при 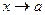
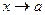
· Если f(x) — б/м при 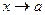
· Если при 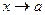

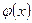
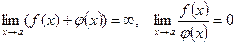
· Если f(x) — б/м при 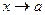
· Если f(x) — б/б при 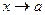
Теоремы о пределах.
1. Если f(x) имеет предел при 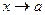
2. Предел суммы функций равен сумме пределов этих функций.
3. Предел произведения функций равен произведению пределов этих функций.
4. Предел частного двух функций равен частному пределов этих функций.
5. Постоянный множитель можно выносить за знак предела
6. Если n – натуральное число, то 
1) 

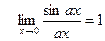
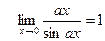
2) 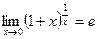

ПРИМЕР 1.На основании определения предела переменной величины доказать, что
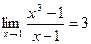
Решение: На основании определения предела переменной величины

ПРИМЕР 2.Найти пределы функции:
а) 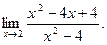
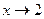
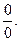
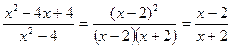
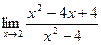
б) 
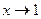
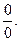
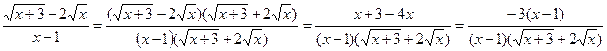

в) 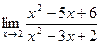
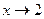
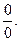
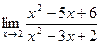
г) 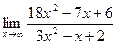

Решение: Сведем к бесконечно малым величинам, разделив каждое слагаемое числителя и знаменателя на наибольшую степень, т.е. х 2 .
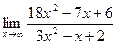

так как при 
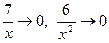
д) 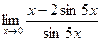
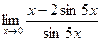
е) 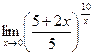
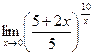
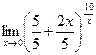
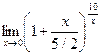
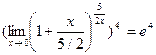
ж) 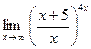


💥 Видео
Видеоурок "Гипербола"Скачать

213. Фокус и директриса параболы.Скачать

Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

§24 Каноническое уравнение параболыСкачать

§29 Эксцентриситет гиперболыСкачать

ГиперболаСкачать

Семинар кривые второго порядка 1Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Лекция 14, 2021. Вывод уравнения эллипса и гиперболыСкачать

Фокус и директриса параболы 1Скачать

Кривые 2 порядка: директрисы, полярное и общее уравнения | 15 | Константин Правдин | ИТМОСкачать

Кривые второго порядкаСкачать

11 класс, 52 урок, ЭллипсСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать