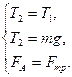Написать уравнение движения для шарика (6 видео)

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

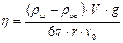
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Содержание

Ламинарное движение шарика в жидкости. Формула Стокса
§ 1.3. Уравнение движения математического маятника
Уравнение для тангенциальной составляющей ускорения
🔥 Видео

Видео:Физика - уравнения равноускоренного движенияСкачать

Ламинарное движение шарика в жидкости. Формула Стокса

Стоксом было получено строгое решение задачи о ламинарном обтекания шарика безграничной жидкостью. В этом случае сила сопротивления F определяется формулой

, (14)

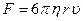
где h – коэффициент внутреннего трения жидкости, u –скорость шарика, r – радиус шарика.

Гидродинамический вывод формулы Стокса довольно сложен. Поэтому ограничимся анализом задачи с помощью теории размерности. На основании физических соображений и опыта можно считать, что сила F должна определяться параметрами h, u, r и плотностью жидкости r_ж. Искомый закон следует искать в виде степенного соотношения

, (15)

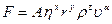
где А – безразмерный множитель, а x, y, z и a – подлежащие определению показатели степени. Выбор показателей степени определяется из того условия, что размерности левой и правой частей должны совпадать. Из опыта известно, сто при малых скоростях движения тела (ламинарное течение) сила сопротивления пропорциональна скорости (показатель степени a=1). Приравнивая показатели степени по массе, длине и времени в левой и правой частях уравнения (15), получим

1 = x + z, 1 = -x + 1 + y — 3z, -2 = -x — 1; (16)

x = 1, y = 1, z = 0. (17)

Таким образом получим

Безразмерный множитель А не может быть определен из соображения размерности, но строгое решение этой задачи дает для этого множителя значение 6p.

Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют сила тяжести, архимедова сила и сила вязкого трения, зависящая от скорости u. На основании второго закона механики будем иметь

, (19)

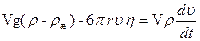
где V – объем шарика, r – его плотность, r_ж – плотность исследуемой жидкости, g – ускорение силы тяжести.

Решая это уравнение найдем

, (20)

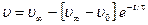
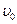
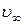
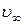
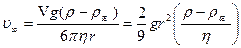
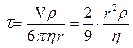
где – скорость шарика в момент начала его движения, которая в опытах обычно равна нулю, – установившаяся скорость движения шарика, t – время релаксации. При этом величины и t соответственно равны

; . (21)

Из уравнения (20) видно, что скорость шарика экспоненциально приближается к установившейся скорости 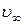. Установление скорости определяется временем релаксации t. Если время падения шарика в несколько раз больше времени релаксации (t>>t), то процесс установления скорости можно считать закончившимся.

Поэтому для некоторой части пути, ограниченной метками А и В, где движение шарика будет равномерным, скорость шарика равна

где l – расстояние, t – время падения шарика между метками А и В.

Подставляя значение скорости в уравнение (21), получим:

. (23)

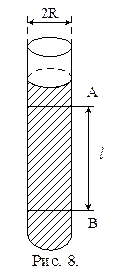
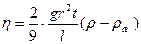
Данное уравнение справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние стенок, т.е. ввести поправки на влияние боковых стенок. Формула для определения коэффициента вязкости с учетом поправок принимает следующий окончательный вид:

. (24)

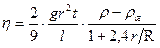
Соотношение (24) используется для определения вязкости жидкостей методом Стокса. Опуская шарик радиусом r в сосуд с исследуемой жидкостью, и измеряя время t прохождения шариком некоторого расстояния l можно найти коэффициент внутреннего трения жидкости h.

При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Известно, что характер обтекания определяется значением числа Рейнольдса, которое определяется из формулы (6)

. (25)

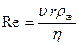
Для тел сферической формы обтекание будет ламинарным при условии Re

Дата добавления: 2015-12-16 ; просмотров: 5318 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение графических задач на равномерное движениеСкачать

§ 1.3. Уравнение движения математического маятника

Рассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Можно пренебречь и ее массой по сравнению с массой шарика. Таким образом, вместо реального маятника — шарика определенного размера на нити, которая, конечно, немного деформируется при движении и имеет массу, мы вправе рассматривать простую модель: материальную точку, подвешенную на нерастяжимой невесомой нити. Такая модель маятника называется математическим маятником в отличие от реального маятника, называемого физическим. Маленький шарик на длинной тонкой нити должен вести себя практически так же, как и математический маятник. Выведем маятник из положения равновесия и отпустим. На шарик будут действовать две силы: сила тяжести = m, направленная вертикально вниз, и сила упругости нити _у, направленная вдоль нити (рис. 1.8).

Конечно, при движении маятника на него еще действует сила трения. Но мы будем считать ее пренебрежимо малой.

Силу тяжести удобно разложить на две составляющие: тангенциальную _τ, направленную по касательной к траектории перпендикулярно к нити, и нормальную _n, направленную вдоль нити. Сила упругости нити _у и составляющая силы тяжести _п перпендикулярны к скорости маятника и сообщают ему нормальное ускорение. Действие этих сил не меняет скорости маятника по модулю, а приводит лишь к изменению направления скорости. Вектор скорости непрерывно поворачивается, так что в любой момент времени скорость направлена по касательной к дуге окружности — траектории маятника.

Тангенциальная составляющая _τ силы тяжести создает тангенциальное ускорение, характеризующее изменение скорости по модулю. Она всегда направлена к положению равновесия, и именно она вызывает колебания маятника.

При колебаниях шарика на нерастяжимой нити он всегда движется по дуге окружности, радиус которой равен длине нити l. Поэтому положение шарика в любой момент определяется одной величиной — углом α отклонения нити от вертикали (см. рис. 1.8). Будем считать угол α положительным, если маятник отклонен вправо от положения равновесия, и отрицательным, если он отклонен влево.

Уравнение для тангенциальной составляющей ускорения

Тангенциальная проекция силы тяжести в момент, когда нить маятника отклонена от положения равновесия на угол α, выражается так:

(Мы считаем значение проекции положительным, если составляющая силы направлена слева направо.) Знак «-» в уравнении (1.3.1) стоит из-за того, что _τ и α имеют противоположные знаки. При отклонении маятника вправо (α > 0) составляющая _τ силы тяжести направлена влево и ее проекция отрицательна: _τ 0.

Согласно второму закону Ньютона

Разделив левую и правую части этого уравнения на m, получим:

До сих пор считалось, что углы отклонения нити от вертикали могут быть любыми, в дальнейшем будем считать их малыми. При малых углах, если выражать угол α в радианах, sin α ≈ α. Следовательно,

Смещение шарика маятника от положения равновесия можно характеризовать не только углом, но и величиной, измеряемой длиной дуги ОА (см. рис. 1.8), взятой со знаком «+», если шарик смещается от положения равновесия вправо, и со знаком «-», если он смещается влево. Очевидно, что

где s — длина дуги ОА.

Подставив в уравнение (1.3.4) это значение α, получим:

приходим к окончательному виду уравнения движения маятника при малых углах отклонения от положения равновесия:

Это уравнение имеет такой же вид, как и уравнение (1.2.6) движения шарика, прикрепленного к пружине. Здесь только вместо проекции ускорения а_x стоит тангенциальное ускорение а_τ и вместо координаты х — величина s. Да и зависит уже не от жесткости пружины и массы груза, а от ускорения свободного падения и длины нити. Но по-прежнему ускорение прямо пропорционально смещению (определяемому дугой) шарика от положения равновесия. Если бы мы в случае маятника обозначили тангенциальное ускорение через а_x, а дугу через х, то оба уравнения (1.2.6) и (1.3.8) были бы неразличимы.

Важное заключение. Мы пришли к замечательному выводу: уравнения движения, описывающие колебания таких различных систем, как груз на пружине и маятник, одинаковы. Это означает, что движение шарика и колебания маятника происходят одинаковым образом. Смещения груза на пружине и шарика маятника от положения равновесия изменяются со временем по одному и тому же закону, несмотря на то, что силы, вызывающие колебания, имеют различную физическую природу. В первом случае это сила упругости, а во втором — составляющая силы тяжести.

Уравнение движения (1.2.6), как и уравнение (1.3.8), выглядит внешне очень просто: ускорение прямо пропорционально координате. Но решить его, т. е. определить, как меняется координата колеблющегося тела с течением времени, не просто. До сих пор в механике мы в основном рассматривали движение с постоянным ускорением. При колебаниях же ускорение меняется со временем, так как меняется сила, действующая на тело.