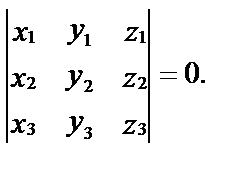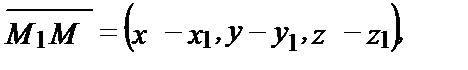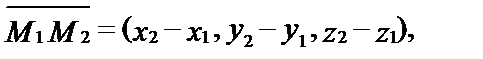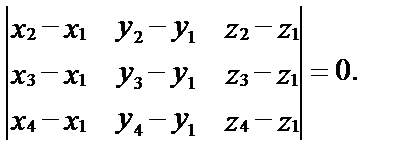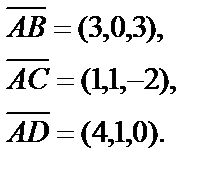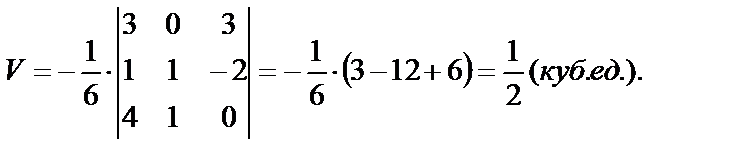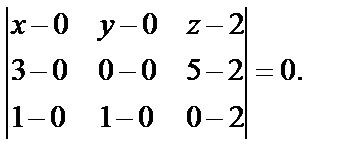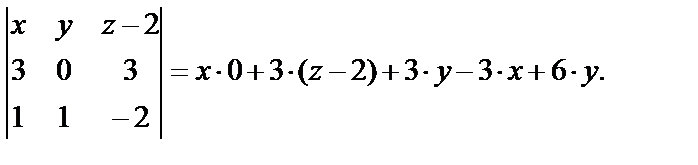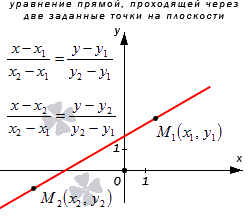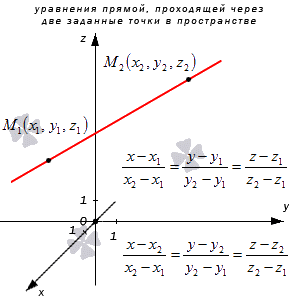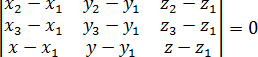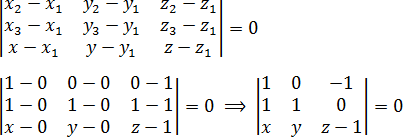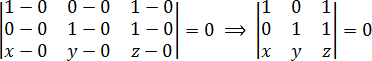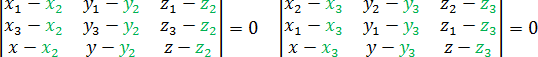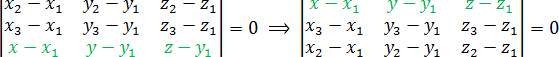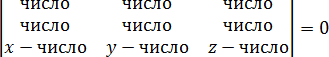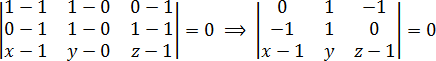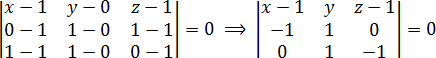Написать с помощью определителя 3 порядка уравнение прямой проходящей через точки (7 видео)

Применение определителей к решению некоторых задач аналитической геометрии

На плоскости уравнение прямой, проходящей через две данные точки, имеет вид:

– формула (3) в п. 4

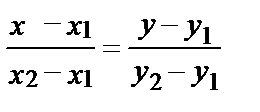
Это же уравнение можно получить и с помощью определителя, а именно:

(10)

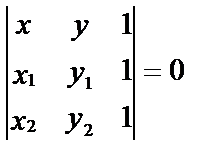
Чтобы убедиться, что это уравнение действительно определяет прямую, достаточно применить правило Сарруса к определителю.

С помощью формулы (10) легко получить условие принадлежности трех точек одной прямой, Если точки М₁(х₁, у₁), М₂(х₂, у₂) и М₃(х₃, у₃) лежат на одной прямой, то справедливо равенство

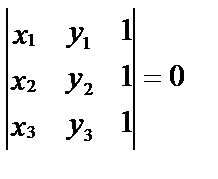
Без доказательства приведем формулу для вычисления площади треугольника по координатам его вершин:

или (11)

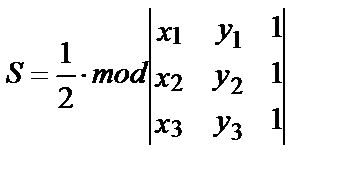
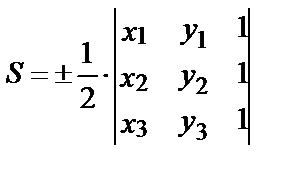
При вычислении определителя может получиться отрицательное число и, чтобы площадь S была положительным числом, следует взять либо абсолютную величину (модуль) определителя, либо выбрать нужный знак.

В векторной алгебре широко используются определители при рассмотрении таких операций как векторное произведение двух векторов, смешанное произведение трех векторов и т. д. Не имея возможности остановиться подробно на этих вопросах, мы тем не менее приведем некоторые формулы, которые используются при решении геометрических задач.

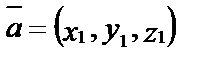
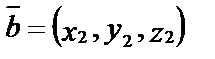
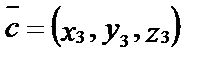
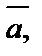
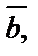
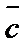
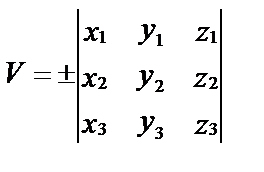
Если известны координаты трех векторов , , , то объем V параллелепипеда, построенного на векторах , как на ребрах, вычисляется по формуле:

. (12)

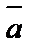
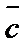
Тогда очевидно, что если векторы , и компланарны (т. е. лежат в одной или в параллельных плоскостях), то

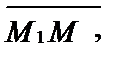
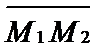
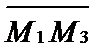
При помощи этой формулы получим уравнение плоскости, проходящей через три данные точки М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂), М₃(х₃, у₃, z₃). Векторы будут компланарны, если точка М(х, у, z) – любая точка этой плоскости.

Запишем координаты этих векторов:

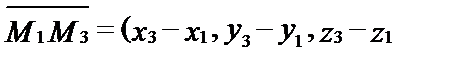
Используя условие компланарности, получим уравнение плоскости, проходящей через три данные точки:

(13)

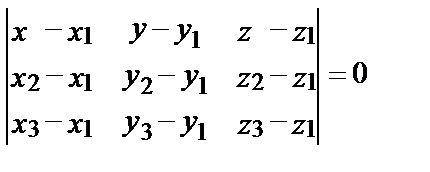
Наконец, условие принадлежности четырех данных точек М₁, М₂, М₃ и М₄ одной плоскости имеет вид:

Даны вершины пирамиды А(0, 0, 2), В(3, 0, 5), С(1, 1, 0), D(4, 1, 2). Вычислить объем пирамиды и составить уравнение ее грани АВС.

Найдем координаты векторов, выходящих из одной вершины:

Эти векторы служат ребрами пирамиды, объем которой составляет шестую часть объема параллелепипеда, построенного на тех же ребрах. Поэтому объем V пирамиды:

Заметим, что поскольку определитель равен –3, следует в формуле для вычисления объема выбрать знак минус. Итак, объем V= 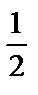куб. ед.

Грань АВС лежит в плоскости, проходящей через точки А(0, 0, 2), В(3, 0, 5), С(1, 1, 0).

Поэтому уравнение этой плоскости:

или

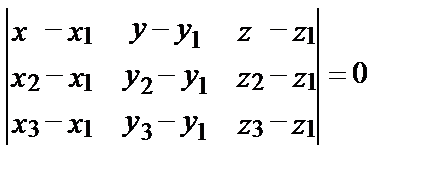
Итак, уравнение искомой плоскости 3z – 6 + 3у – 3х + 6у = 0 или

Содержание

Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Уравнение прямой, проходящей через две заданные точки на плоскости
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Задача C2: уравнение плоскости через определитель
Уравнение плоскости по трем точкам
Уравнение плоскости через определитель
Откуда берется формула с определителем?
Замена точек и строк определителя
🌟 Видео

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Видео:Составляем уравнение прямой по точкамСкачать

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

Видео:Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Задача C2: уравнение плоскости через определитель

В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:

Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:

Ax + By + Cz + D = 0

где числа A , B , C и D — коэффициенты, которые, собственно, и требуется найти.

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием обоснований и доказательств.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

Задача. Составьте уравнение плоскости, проходящей через точки:

Составляем определитель и приравниваем его к нулю:

a = 1 · 1 · ( z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · ( z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (− x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Задача. Составьте уравнение плоскости, проходящей через точки:

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − ( x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, рекомендуется — чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит а в какой — Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Откуда берется формула с определителем?

Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.

Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

Берем любую точку из первой тройки (например, и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:

Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка как раз то, что мы искали.

Видео:§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax + By + Cz + D = 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Задача. Составьте уравнение плоскости, проходящей через точки:

Итак, рассматриваем 4 точки:

Для начала составим стандартный определитель и приравниваем его к нулю:

a = 0 · 1 · ( z − 1) + 1 · 0 · ( x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · ( x − 1) + 1 · (−1) · ( z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

Все, мы получили ответ: .

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными не внизу, а вверху:

Вновь раскрываем полученный определитель:

a = ( x − 1) · 1 · (−1) + ( z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = ( z − 1) · 1 · 0 + y · (−1) · (−1) + ( x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Мы получили точно такое же уравнение плоскости: Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку но вполне можно было взять В общем, любую точку с известными координатами, лежащую на искомой плоскости.