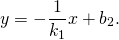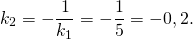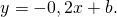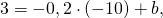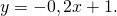Альтернативная формула
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).
Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /9x – 1 /3 (a = 4 /9). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .
Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой
В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
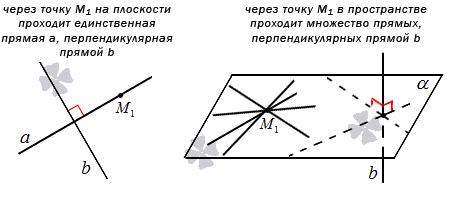
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .
По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .
Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .
Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .
Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.
После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .
Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Решение примеров
Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.
Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .
Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .
Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0
Полученное уравнение является искомым.
Ответ: 3 x + y — 12 = 0 .
Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .
Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.
Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .
Ответ: x 2 = y — 1 .
Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .
Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Уравнение перпендикулярной прямой
Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?
Пусть y=k1x+b1 — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид
Если эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b.
1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.
Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то
Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид
Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:
Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)
2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).
Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.
Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.
3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).
Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.
Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.
🎬 Видео
Составляем уравнение прямой по точкамСкачать
Часть 8 Уравнение прямой проходящей через точку и перпендикулярную к заданной прямойСкачать
Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать
12. Уравнения прямой в пространстве Решение задачСкачать
Уравнение параллельной прямойСкачать
Математика без Ху!ни. Уравнение плоскости.Скачать
9 класс, 7 урок, Уравнение прямойСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать
Уравнение прямой, проходящей через две точки, и прямой, перпендикулярной заданной прямойСкачать
Уравнение прямой, проходящей через данную точку в данном направленииСкачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
Видеоурок "Уравнение прямой, проходящей через две точки"Скачать
Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать
№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать
Уравнение прямой, проходящей через две точкиСкачать
