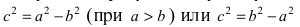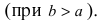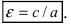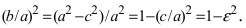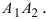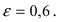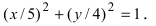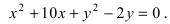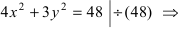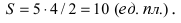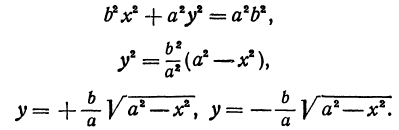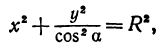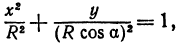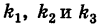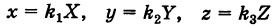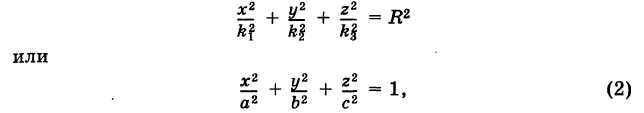Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 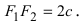
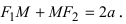
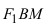
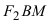
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 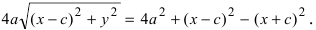
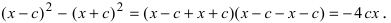
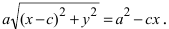
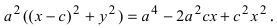
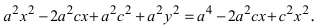
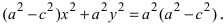
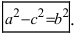
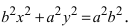
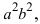
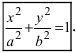
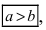
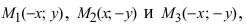
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 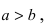
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 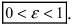
Если 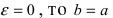
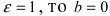
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 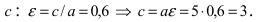
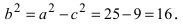
Пример:
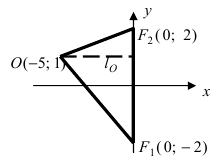
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 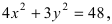
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
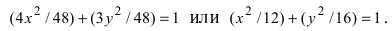
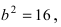
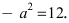
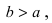
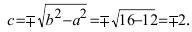
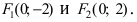
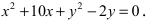
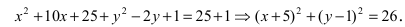
Построим в декартовой системе координат треугольник 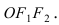
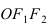
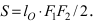
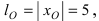
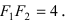
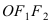
- Эллипс в высшей математике
- Уравнение эллипсоида
- Написать каноническое уравнение симметричного относительно осей координат
- Кривые второго порядка. Эллипс: формулы и задачи
- Понятие о кривых второго порядка
- Эллипс, заданный каноническим уравнением
- Решить задачи на эллипс самостоятельно, а затем посмотреть решение
- Продолжаем решать задачи на эллипс вместе
- 💡 Видео
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Эллипс в высшей математике
где 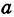
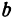
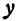
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
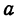

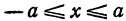
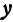
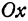
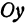
При 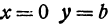
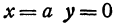
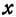

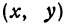
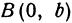
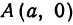
Полученная линия называется эллипсом. Число 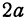
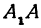
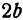
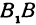
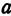
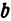
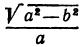
Пример:
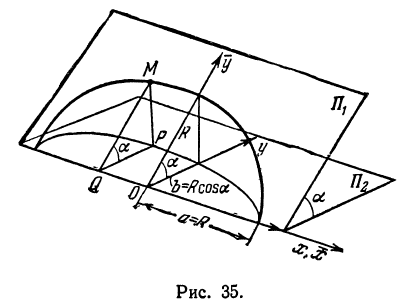
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 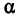
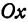
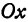
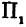
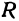
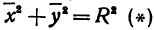
Пусть точка 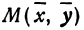
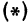
Обозначим проекцию точки 
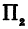
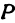
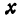
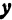


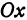
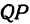
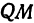
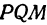
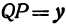
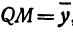
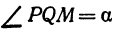
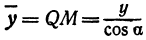


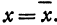
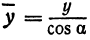
а это есть уравнение эллипса с полуосями 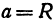
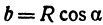
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 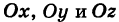
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 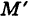
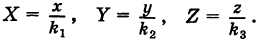
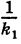
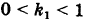
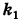
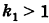
Подставляя эти формулы в уравнение (1), будем иметь
где 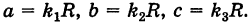
Величины 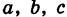
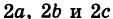
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Видеоурок "Гипербола"Скачать

Написать каноническое уравнение симметричного относительно осей координат
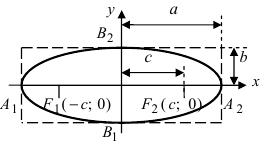
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а сумму расстояний от произвольной точки эллипса до фокусов – через 2 a . По определению 2 a > 2 c , то есть a > c .
Выберем систему координат так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпадало с серединой отрезка F 1 F 2 . Тогда фокусы имют координаты: F 1 (– c ;0) и F 2 ( c ;0) . Пусть M ( x ; y ) – произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Это уравнение равносильно первоначальному. Оно называется каноническим уравнением эллипса – кривой второго порядка .
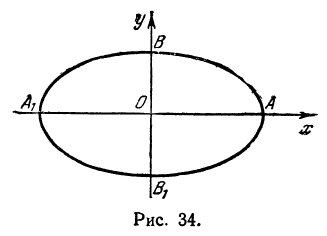
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (2.17) содержит x и y только в четных степенях, поэтому если точка ( x ; y ) принадлежит эллипсу, то ему также принадлежат точки (– x ; y ), ( x ;– y ), (– x ;– y ) . Отсюда: эллипс симметричен относительно осей 0 x и 0 y , а также относительно точки O (0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив y = 0, найдем точки A 1 ( a ; 0) и A 2 (– a ; 0), в которых ось 0 x пересекает эллипс. Положив в уравнении (2.17) x = 0, находим точки пересечения эллипса с осью 0 y : B 1 (0; b ) и B 2 (0;– b ). Точки A 1 , A 2 , B 1 , B 2 называются вершинами эллипса. Отрезки А1А2, В1В2, а также их длины 2 a и 2 b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.:
Следовательно, все точки эллипса лежат внутри прямоугольника, ограниченного прямыми x = ± a и y = ± b .
4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x | возрастает, | y | уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму овальной замкнутой кривой. Форма эллипса зависит от отношения 


Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε = 0 эллипс превращается в окружность.
Прямые 
Если r – расстояние от произвольной точки до какого–нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение 

Из равенства a 2 – c 2 = b 2 следует, что a > b . Если же наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2 b лежит на оси 0 y , а малая ось 2 a – на оси 0 x . Фокусы такого эллипса находятся в точках F 1 (0; c ) и F 2 (0;– c ) , где 
Пример 2.5. Составить уравнение линии, для каждой точки которой отношение расстояний от нее до точки A (3;0) и до прямой x = 12, равно числу ε =0,5 . Полученное уравнение привести к простейшему виду .
Решение . Пусть M ( x ; y ) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр MB на прямую . Тогда точка B( 12;y) . По условию задачи 
По формуле расстояния 
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой) 
Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины.
Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a = 6 378 245 м, b = 6 356 863 м, α = 1: 298,3.
Линия, проходящая вертикально через центр эллипсоида является полярной осью. Линия, проходящая через центр эллипсоида, перпендикулярно к полярной оси, – экваториальной осью. При пересечении поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно к полярной оси, образуется окружность, называемая экватором. Окружность, полученная от пересечения поверхности эллипсоида плоскостью, параллельной плоскости экватора, называется параллелью. Линия пересечения поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной линией называется географической широтой. Для определения долгот точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, называется географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости – фокусов, есть величина постоянная, равная 2 a .
Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2 c , а модуль разности расстояний от каждой точки гиперболы до фокусов через 2 a . По определению 2 a 2 c , то есть a c .
Выберем систему координат x 0 y так, чтобы фокусы F 1 и F 2 лежали на оси 0 x , а начало координат совпало с серединой отрезка F 1 F 2 . Тогда фокусы будут иметь координаты F 1( c ;0 ) и F 2 (– c ;0 ). На этой основе выведем уравнение гиперболы. Пусть M ( x ; y ) – ее произвольная точка . Тогда по определению | MF 1 – MF 2 |= 2 a , то есть 
где b 2 = a 2 – c 2 . Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического уравнения.
1. Уравнение (2.18) содержит x и y только в четных степенях. Следовательно, гипербола симметрична относительно осей координат 0 x и 0 y , и относительно точки O (0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (2.18) y =0 , находим две точки пересечения гиперболы с осью 0 x : A 1 ( a ; 0) и A 2 (– a ; 0).
Положив в (2.18) x = 0, получаем y 2 = – b 2 , чего быть не может. Т.е. гипербола ось 0 y не пересекает.
3. Из уравнения (2.18) следует, что уменьшаемое 
4. Из уравнения (2.18) гиперболы видно, что когда | x | возрастает, то | y | также возрастает . Это следует из того, что разность 
Прямая L называется асимптотой некоторой неограниченной кривой , если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном удалении т очки M вдоль кривой от начала координат.
Покажем, что гипербола 

Возьмем на прямой 

Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка | MN | стремится к нулю. Так как | MN | больше расстояния d от точки M до прямой L, то d стремится к нулю тем более ( и подавно) . Следовательно, прямые 
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы .
Эксцентриситет гиперболы – отношение расстояния между фокусами к величине её действительной оси, обозначается ε : 


Эксцентриситет равносторонней гиперболы равен 

Прямые 


Уравнение 
Значит , гиперболы 
Примечание. Если у кривой 2–го порядка смещен центр в некоторую точку O ’ ( x 0 ; y 0 ) , то она называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме: «Исследование общего уравнения 2–ой степени» (смотри схему 10), частными случаями которого являются данные формулы.
Видео:11 класс, 10 урок, Осевая симметрияСкачать

Кривые второго порядка. Эллипс: формулы и задачи
Видео:Видеоурок "Канонические уравнения прямой"Скачать

Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
💡 Видео
Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

§22 Исследование канонического уравнения гиперболыСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать

ЭллипсСкачать

Как найти точку, симметричную точке А(3;4) относительно начала координат. Как решать. Простой способСкачать

Симметрия относительно прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

§25 Исследование канонического уравнения параболыСкачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

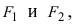
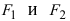
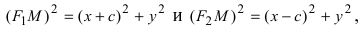
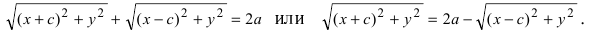
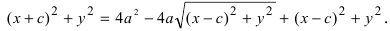
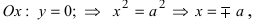 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 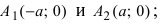
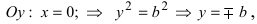 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 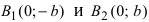 (Рис. 30).
(Рис. 30).