Написать каноническое уравнение эллипса если его большая полуось равна 6 а эксцентриситет равен 0 5

Математика | 5 — 9 классы

Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 6, а эксцентриситет ε = 3 / 5.

Канонический вид эллипса имеет вид :

Нужно найти а и b.

Найдем фокальное расстояние$c= frac$.

Зная формулу нахождения b, получим :

Теперь можем составить каноническое уравнение эллипса :

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Составить канонические уравнения : а) эллипса ; б)гиперболы ; в) параболы?

Составить канонические уравнения : а) эллипса ; б)гиперболы ; в) параболы.

Где А, В — точки, лежащие на кривой, F — фокус, a — большая (действительная) полуось, b — малая (мнимая) полуось, Е — эксцентриситет, у = + — kx — уравнения асимптот гиперболы, D — директриса кривой, 2с — фокусное расстояние.

A) 2a = 22, Е = √57 / 11 ; b) k = 2 / 3 ; 2c = 10 √13 ; c) ось симметрии Ox и А(27 ; 9).

Видео:§28 Эксцентриситет эллипсаСкачать

Написать канонические уравнение гиперболы, если известно, что а)расстояние между фокусами равно 10 и эксцентриситет равен 5 / 3?

Написать канонические уравнение гиперболы, если известно, что а)расстояние между фокусами равно 10 и эксцентриситет равен 5 / 3.

Видео:Написать каноническое уравнение эллипса, если известны b и cСкачать

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1?

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1.

Найдите его эксцентриситет.

Видео:§18 Каноническое уравнение эллипсаСкачать

Построить эллипс 25x ^ 2 + 16y ^ 2 = 400?

Построить эллипс 25x ^ 2 + 16y ^ 2 = 400.

Найти координаты его фокусов, длину осей и эксцентриситет.

Написать уравнение прямой, проходящей через его правый фокус и точку(1 ; — 3).

Пропустил тему и блин застреваю на каждом шагу(.

Видео:166. Найти каноническое уравнение эллипса.Скачать

Составить уравнение эллипса, фокальное расстояние которого равно 16 и эксцентриситет равен 4 / 5?

Составить уравнение эллипса, фокальное расстояние которого равно 16 и эксцентриситет равен 4 / 5.

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Составить уравнение гиперболы с фокусами на оси Ох, если длина ее действительной оси равна 12, а расстояние между фокусами равно 20?

Составить уравнение гиперболы с фокусами на оси Ох, если длина ее действительной оси равна 12, а расстояние между фокусами равно 20.

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Составить уравнение эллипса с фокусами на оси Ox, если его большая ось равна 16, а эксцентритет e = 0, 8?

Составить уравнение эллипса с фокусами на оси Ox, если его большая ось равна 16, а эксцентритет e = 0, 8.

Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Написать уравнение эллипса, если известно, что расстояние между фокусами эллипса равно 8, а малая полуось b = 3?

Написать уравнение эллипса, если известно, что расстояние между фокусами эллипса равно 8, а малая полуось b = 3.

Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Найти полуоси, фокусы и эксцентриситет эллипса 4x² + 9y² = 16?

Найти полуоси, фокусы и эксцентриситет эллипса 4x² + 9y² = 16.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Помогите пожалуйста задание решить))))))) Заранее спасибо = )Составить каноническое уравнениеА) эллипсаБ) гиперболыВ) параболы(А, В – точки лежащие на кривой, f — фокус, а — большая (действительная)по?

Помогите пожалуйста задание решить))))))) Заранее спасибо = )

Составить каноническое уравнение

(А, В – точки лежащие на кривой, f — фокус, а — большая (действительная)

полуось, в — малая (мнимая) полуось, е — экцентриситет, у = — + кх — уравнение асимптот

директриса кривой, 2с — фокусное расстояние).

Вопрос Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 6, а эксцентриситет ε = 3 / 5?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Найдём наибольший общий делитель НОД : 184 = 2 * 2 * 2 * 23 253 = 11 * 23 НОД (184 ; 253) = 23 — наибольшее число спортсменов в команде 184 : 23 = 8 маек — в 1 наборе 253 : 23 = 11 футболок — в 1 наборе Т. Е. каждый спортсмен получил в наборе 8 маек..

2 — прямоугольный ; 3 — прямоугольный ; 5 — равнобедренный ; 6 — равносторонний ; 8 — тупоугольный раносторонний ; 9 — прямоугольный равнобедренный ; 10 — остроугольный равносторонний.

2 — прямоугольный 3 — разносторонний 5 — равнобедренный 6 — равноугольный.

Жандос — 167 Алёша — 158 Санжар — 152 Виктор — 149.

Санжар — 152см, так как он третий по росту, а Алеша — 158см, так как он второй по росту.

Сначала, используя условие задачи, находим скорость теплохода по течению (105 : 5 = 21 км / ч) и против течения (105 : 7 = 15 км / ч). Пусть собственная скорость теплохода — х, а скорость течения — у. Составим систему уравнений : Решим систему, сл..

Число 180. 1 + 8 = 9 9 * 20 = 180.

Воттттт 5 + 1 + 4 + 3 — 2 = 12.

A) 97 + 3 + 55 = 155 24 + 6 + 38 + 52 + 17 = 137 200 + 345 = 545 425 + 75 + 143 = 643.

У Маши — переменная y является кол — вом конфет. У Кирилла — пусть будет переменная x У Коли — (y + x) — 15 Если я так понял.

Видео:ЭллипсСкачать

Кривые второго порядка. Эллипс: формулы и задачи

Видео:Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

,

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Видео:Видеоурок "Эллипс"Скачать

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

,

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

.

Точки и , обозначенные зелёным на большей оси, где

,

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

.

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

.

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

.

Получаем фокусы эллипса:

Видео:Видеоурок "Гипербола"Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Видео:11 класс, 52 урок, ЭллипсСкачать

Продолжаем решать задачи на эллипс вместе

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

,

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

,

где и — расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

.

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

.

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

,

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

Видео:213. Фокус и директриса параболы.Скачать

Написать каноническое уравнение эллипса если его большая полуось равна 6 а эксцентриситет равен 0 5

Вопрос по математике:

Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0,8. Найти расстояние между фокусами эллипса

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

📹 Видео

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

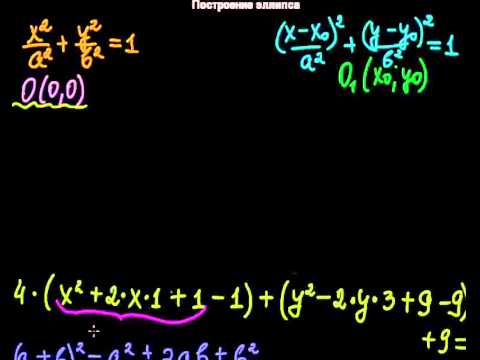
Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

§20 Построение эллипсаСкачать