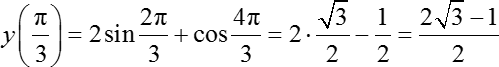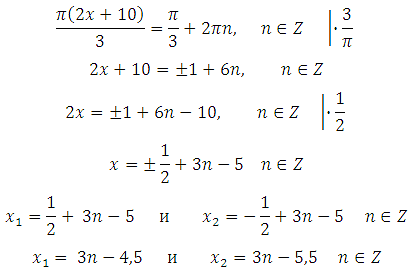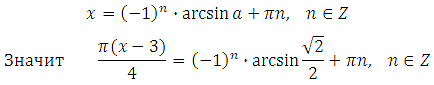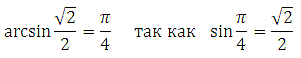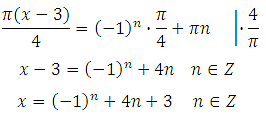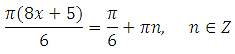Сегодня у нас заключительный урок на производные из ЕГЭ по математике. И как всегда по традиции последняя задача будет немножко нестандартной. Итак:
Задача B15. Найдите наибольшее значение функции на отрезке [0; π/3]:
y = 2sin 2 x + cos 4 x
- Общая схема вычисления наибольшего значения функции
- Экстремумы функции на отрезке: пояснение
- Локальный и глобальный экстремум функции: в чем разница?
- Решение задачи B15 с тригонометрией
- Производная тригонометрической функции
- Производная функции при линейной замене
- Считаем нули производной — точки экстремума
- Производная тригонометрической функции: отбор корней на отрезке
- Вычисление наибольшего значения функции
- Вычисление сложных значений тригонометрической функции
- Ключевые моменты в задачах B15 на производную функции
- Особенности записи корней тригонометрического уравнения
- Тригонометрические уравнения
- Тригонометрические уравнения
- Четность тригонометрических функций
- Тригонометрические тождества
- Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
- Обратные тригонометрические функции и простейшие тригонометрические уравнения.
- Арккосинус
- Арксинус
- Арктангенс
- 🔥 Видео
Видео:Найдите наибольшее и наименьшее значения тригонометрического выражения 1-4cosa. Как решить? Просто!Скачать

Общая схема вычисления наибольшего значения функции
Перед тем, как мы начнем решать эту задачу, хотел бы напомнить вам общий универсальный алгоритм поиска наибольшего и наименьшего значения функции на отрезке. Он состоит из 4 шагов:
1. Первый шаг состоит в том, что нужно найти производную нашей функции: y ‘ = ?
2. Второй шаг — производную мы приравниваем к нулю в результате решения у нас получится один или несколько корней: x , x , .
3. Затем берем эти корни и оставляем только те из них, которые лежат на отрезке, указанном в условии задачи — в нашем случае речь идет об отрезке [0; π/3]. Другими словами, мы вычеркиваем все корни, которые не лежат на интересующем нас отрезке: x , x ∈ [0; π/3].
4. Наконец, подставляем концы отрезка, а также оставшиеся корни в нашей исходное уравнение. Другими словами, мы находим y (0); y (π/3); y ( x 1); y ( x 2), т. е. значение функции в нулях производной.
Это стандартная схема, и мы применяли ее уже много раз.
Видео:ЕГЭ №9. Тригонометрические выражения.Тригонометрические уравнения | Математика | TutorOnlineСкачать

Экстремумы функции на отрезке: пояснение
Естественно, при взгляде на этот алгоритм у многих учеников сразу возникают вопросы. Первый и самый распространенный: «Почему это мы подставляем в нашу функцию концы отрезка? Неужели недостаточно просто посчитать функцию в нулях производной?»
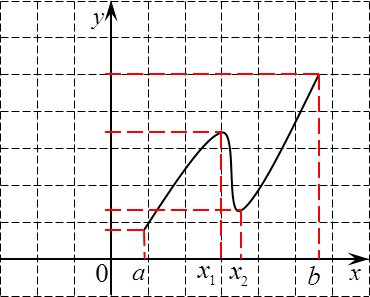
К сожалению, недостаточно. Взгляните вот на такую функцию:
На этом рисунке видно, что наибольшее значение функции достигается именно в правом верхнем конце отрезка — в точке b , а никак не в точке x 1, которая является точкой максимума и, соответственно, возникает при решении уравнения y ‘ = 0. То же самое и с наименьшим значением — оно достигается в точке a , но ни в коем случае не в точке x 2, которая также возникнет при решении y ‘ = 0.
Локальный и глобальный экстремум функции: в чем разница?
Вспомните определение производной и точки экстремума: в данном случае точка x 1 будет являться точкой локального максимума, т. е. на некотором интервале, достаточно небольшом, именно на этой точке будет приниматься наибольшее значение. То же самое касается и точки x 2. На некотором небольшом интервале, т. е. на определенном отступе от этой точки вправо или влево функция действительно будет принимать наименьшее значение именно в точке x 2.
Однако на глобальном отрезке никто этого не гарантировал. И часто случается так, что настоящее наибольшее или наименьшее значение функции достигается именно на концах рассматриваемого отрезка. Особенно это качается задач B15, которые любят давать на пробниках и разных демонстрационных ЕГЭ по математике.
Наибольшее или наименьшее значение функции совсем не обязательно достигается в нулях производной. Очень часто такие значения возникают на концах отрезка, где производная отлична от нуля.
В общем, чтобы подстраховаться и не допустить обидных ошибок на настоящем экзамене, настоятельно рекомендую вам считать значения функции не только в нулях производной, но и на концах отрезка, т. е. в нашем случае в точках х = 0 и х = π/3.
Видео:Найдите значение тригонометрического выраженияСкачать

Решение задачи B15 с тригонометрией
С теорией разобрались, давайте решать нашу задачу. Для начала нам нужно посчитать производную функции:
y = 2sin 2 x + cos 4 x
Производная тригонометрической функции
y ‘ = (2sin 2 x + cos 4 x )’ = (2sin 2 x )’ + (cos 4 x )’
И вот тут возникает проблема в данной задаче: дело в том, что внутри синуса и косинуса стоит не переменная х, а выражение 2х и даже 4х.
Как поступать с такими конструкциями? Конечно, можно воспользоваться производной сложной функции, посчитать и в итоге получить правильное значение, но давайте не будем лезть в дебри, а вспомним замечательную формулу, которая рассматривалась не нескольких уроках, посвященным подготовке к ЕГЭ по математике. Формула следующая:
x → kx + b
( f ( x ))’ → k ( f ‘ ( kx + b ))
Другими словами, замена переменной функции не проходит для всей функции бесследно. В случае, если вместо х мы подставляем линейную функцию, то перед новой производной появляется коэффициент.
Линейная замена переменной приводит лишь к одному дополнительному множителю в производной. Никаких сложных формул при линейной замене применять не нужно!
Это частный случай производной сложной функции. Однако сложные функции в реальном ЕГЭ не встречаются. Поэтому вам достаточно будет знать упрощенную конструкцию, которую мы записали. Ее очень легко применять.
Производная функции при линейной замене
Давайте посчитаем производную sin 2 x . Для этого вспомним такое:
Тогда производная от sin 2 x будет выглядеть так:
(sin 2 x )’ = 2 · cos 2 x
Все, производная 2sin 2 x найдена. Аналогично давайте разберемся и с производной cos 4 x :
(cos 4 x )’ = 4 · (−sin 4 x ) = −4 sin 4 x
А теперь собираем это все в одну конструкцию и получаем:
y ‘ = 4 cos 2 x − 4 sin 4 x
Считаем нули производной — точки экстремума
Итак, первый шаг нашего алгоритма выполнен, мы нашли производную. Теперь приравниваем эту производную к нулю и решаем полученное уравнение:
2 cos 2 x − 4 sin 4 x = 0
Перед нами обычное тригонометрическое уравнение и все, что нам требуется сделать в нем — это свести все тригонометрические функции к одному и тому же аргументу. Как правило, в таких задачах следует стремиться к наименьшему аргументу. Поэтому вспомним формулу двойного угла:
sin 2λ = 2 sin λ cos λ
В нашем случае это будет выглядеть так:
sin 4 x = sin 2 · 2 x = 2 · sin 2 x · cos 2 x
Обратите внимание! Мы пишем именно 2х, потому что в исходной формуле, которую мы разложили, вместо переменной λ стоит именно 2х.
Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта. Получим:
4 cos 2 x − 8 sin 2 x cos 2 x = 0
4 cos 2 x (1 − 2 sin 2 x · 1) = 0
Итак, мы разложили наше уравнение на множители. Теперь вспоминаем: произведение равно нулю, когда хотя бы один из множителей равен нулю. Запишем:
cos 2 x = 0
1 − 2 sin 2 x = 0
Первое уравнение решается элементарно:
2 x = π/2 + π n , n ∈ Z
А со вторым уравнением будет немного посложнее:
sin 2 x = 1/2
2 x = π/6 + 2π n
2 x = π − π/6 + 2π n
Напомню, что решение простейших тригонометрических уравнений, которые содержат синус, лучше записывать как совокупность из двух наборов корней.
Однако на этом решение уравнения еще не закончилось. Взгляните, мы нашли только 2х, а нужно найти просто х. Находим:
x = π/3 + π n /2;
x = π/12 + πn;
x = 5π/12 + π n .
Производная тригонометрической функции: отбор корней на отрезке
Уравнение решено. Переходим к третьему шагу: необходимо отобрать корны, которые лежат на отрезке [0; π/3].
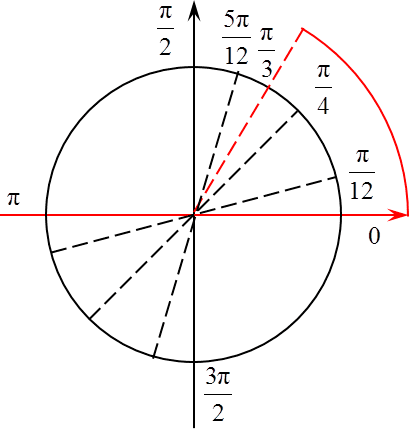
Для этого нам сначала потребуется начертить радар, а потом отметить на мне все три набора корней. На этом же отрезке отмечаем концы отрезка. Получим:
На самом деле из всего этого многообразия нас интересуют лишь две точки: π/4 и π/12. Все, третий шаг выполнен. Мы отобрали корни на отрезке.
Вычисление наибольшего значения функции
А теперь возвращаемся к условию задачи и вспоминаем, что нам нужно найти наибольшее значение функции на отрезке. Т. е. нужно взять функцию
y = 2sin 2 x + cos 4 x
И подставить в нее следующие числа:
- Оба конца нашего отрезка — числа 0 и π/3
- А также два корня производной, которую мы нашли: π/4 и π/12
Затем из полученных четырех значений функции надо выбрать наибольшее.
Давайте решать. В первую очередь предлагаю подставить корни нашей производной, т. е. числа π/4 и π/12. Получим:
y (π/4) = 2 · sin 2 · π/4 + cos 4 · π/4 = 2 · sin π/2 + cos π = 2 · 1 − 1 = 1
Подставляем второе число — x = π/12:
y (π/12) = 2 · sin 2 · π/12 + cos 4 · π/12 = 2 · sin π/6 + cos π/3 = 2 · 1/2 + 1/2 = 1,5
Все, с корнями из производной мы разобрались, теперь считаем значение функции на концах отрезка:
y (0) = 2 · sin 0 + cos 0 = 2 · 0 + 1 = 1
Вычисление сложных значений тригонометрической функции
Теперь подставляем правый конец отрезка:
y (π/3) = 2 · sin 2 · π/3 + cos 4 · π/3 = 2 · sin 2π/3 + cos 4π/3
Оба аргумента и в синусе, и в косинусе являются нестандартными значениями (их нет в классической таблице значений тригонометрических функций), поэтому давайте отметим их на тригонометрическом круге:
С помощью полученных данных вычисляем значение функции:
Это иррациональное число, которое нельзя записать в ответ. Следовательно, оно не является ответом к задаче.
Итого нам на выбор осталось три числа: y = 1; y = 1,5; y = 1. Требуется найти наибольшее значение. Следовательно, ответом будет являться y = 1,5. Все, задача решена.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Ключевые моменты в задачах B15 на производную функции
В заключение хотел бы еще раз обратить ваше внимание на два ключевых факта в решении этой задачи. В первую очередь, речь идет о производной сложной функции. В реальных задачах из ЕГЭ по математике встречается лишь упрощенная версия формулы, которую мы записали в самом начале решения задачи.
Итак, запомните: если в табличной производной заменить переменную х на линейное выражение kx + b , то и в самой производной нужно везде вместо х подставить выражение kx + b . Кроме того, перед самой производной нужно добавить множитель k — тот саамый, который стоял перед х во время замены.
Это универсальное правило, и оно работает всегда. Давайте посмотрим. Например, у нас есть следующая функция:
Возьмем большую степень, чтобы у вас не возникало соблазна раскрывать ее по формулам сокращенного умножения. А теперь мы хотим посчитать производную:
Как это сделать? Очень просто. Вспоминаем: производная функции y = x 101 является табличной и легко считается:
Теперь, если вместо переменной х мы хотим подставить выражение kx + b , например, 5х + 7, то получим, что производная такой функции будет равна:
y ‘ = 101 · (5 x + 7) 101 · 5
Последний множитель «5» появился из-за того, что вместо переменной х мы подставили линейную функцию 5х + 7, т. е. выражение, которое при х содержит множитель 5. Если бы перед их стоял коэффициент k = 10, мы умножили бы производную на 10.
При этом второе слагаемое — число b = 7 — никак не влияет на результат. Т.е. на итоговую производную влияет только коэффициент при х. Запомните это.
Особенности записи корней тригонометрического уравнения
Второй важный момент касается отбора корней и решения тригонометрических уравнений, а конкретно — я бы хотел поговорить про решение тригонометрических уравнений, содержащих синус.
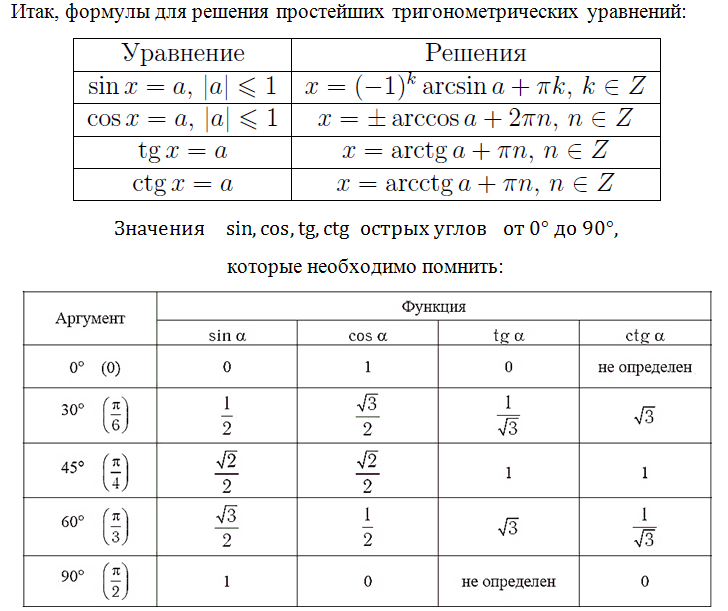
Как обычно нас учат записывать решение таких уравнений? Еще в школьных учебниках можно увидеть формулу:
sin x = a → x = (−1) n · arcsin a + π n , n ∈ Z
Естественно, многие ученики спросят: почему мы не используем эту формулу? Зачем разбивать эту формулу на какую-то совокупность, что-то там считать, усложняя себе задачу?
На самом деле такая запись имеет одно единственное преимущество — краткость. Во всем остальном работать с этой записью — сплошное мучение:
- Непонятно, что делать с множителем (−1) n . Как отмечать постоянно гуляющее то в плюс, то в минус число на тригонометрическом круге?
- Если вы захотите отбирать корни не с помощью тригонометрического круга, а с помощью двойного неравенства, опять же возникает проблема, потому что слагаемое (−1) n · arcsin a нужно будет вычитать из обеих частей неравенства. Затем полученную конструкцию нужно будет разделить на π, и вот тут возникает проблема: а что делать с множителем (−1) n ? Он снова будет мешать нам и служить источником многочисленных ошибок для большинства учеников.
Чтобы избежать этих многочисленных проблем, просто записывайте решение синуса в виде совокупности из двух уравнений, так, как мы и сделали сегодня при решении нашей задачи.
Вот и все замечания. Я специально детально рассказывал каждый шаг решения — настолько детально, что сам допустил ошибку при вычислении производной. Но ничего страшного, мы заметили ошибку вовремя, и поэтому итоговый ответ и все выкладки получись правильными.:)
Желаю вам удачи при решении сложных задач на ЕГЭ по математике, тренируйтесь в решении задач, смотрите видеоуроки и сдавайте ЕГЭ на «отлично». А у меня на этом все.
Видео:№13 Тригонометрические уравнения. Найти наибольшее значение функции y=√3sin5x-cos5xСкачать

Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!
Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Тригонометрические уравнения
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
$1$ радиан $=/≈57$ градусов
Значения тригонометрических функций некоторых углов
| $α$ | $0$ | $/$ | $/$ | $/$ | $/$ | $π$ |
| $sinα$ | $0$ | $/$ | $/$ | $/$ | $1$ | $0$ |
| $cosα$ | $1$ | $/$ | $/$ | $/$ | $0$ | $-1$ |
| $tgα$ | $0$ | $/$ | $1$ | $√3$ | $-$ | $0$ |
| $ctgα$ | $-$ | $√3$ | $1$ | $/$ | $0$ | $-$ |
- Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
- Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется (если же в формуле содержатся углы $90°$ и $270°$ ($π/2$ и $/$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos (90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому перед $sinα$ нужен знак $-$.
$сos (90° + α)= — sinα$ — это конечный результат преобразования
Вычислить $cos 840°$
У косинуса период повторения $2π$ или $360°$, мы можем из угла вычитать количество градусов кратное периоду.
$cos 840°=cos(720°+120°)=cos 120°$
По формуле приведения представим $120°$ как $90°+30°$
$cos(90°+30°) = -sin30= — 0.5$
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс, нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
3. $sin^ α+cos^ α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = / ; t ∈(/;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(/;2π)$ — это четвертая четверть, то синус в ней имеет знак минус.
Обратные тригонометрические функции и простейшие тригонометрические уравнения.
Арккосинус
Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $[0;π]$, косинус которого равен $а$.
$arcos(-a) = π-arccosa$, где $0≤а≤1$
Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение
$cos t =1, t = 2πk;k∈Z$
$cos t = 0, t = /+πk;k∈Z$
$cos t = -1, t=π+2πk;k∈Z$
Найдите наименьший положительный корень уравнения сos $/=-/$
Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на $/$
Чтобы найти наименьший положительный корень, подставим вместо к целые значения
Нам подходит $1.25$ – это и есть результат
Арксинус
Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-/;/]$, синус которого равен $а$.
$arcsin(-a)= — arcsin a$, где $0≤а≤1$
Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:
1. $t_1 = arcsin a+2πk;k∈Z$
$t_2 = (π- arcsin a)+ 2πk;k∈Z$
Арктангенс
$arctg a$ — это такое число, из отрезка $[-/;/]$, тангенс которого равен $а.$
$arctg(-a)= — arctg a$
Уравнение $tg t = a$ имеет решение $t= arctg a+πk;k∈Z$
🔥 Видео
Наибольшее и наименьшее значение функции. 10 класс.Скачать
Как найти наибольшее и наименьшее значения выражения cos α+√3 sin α. Тригонометрия. Простое решениеСкачать

Наибольшее и наим. значения функции на отрезкеСкачать
СЕКРЕТНЫЙ ЛАЙФХАК С ТРИГОНОМЕТРИЕЙ НА ЕГЭ #shorts #математика #егэ #огэ #тригонометрияСкачать

Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезкеСкачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Наибольшее и наименьшее значение функции. Когда есть логарифм.Скачать

Найдите наибольшее значение функции y=12cosx+6√3 x-2√3 π+6 на отрезке [0; π/2]Скачать
![Найдите наибольшее значение функции y=12cosx+6√3 x-2√3 π+6 на отрезке [0; π/2]](https://i.ytimg.com/vi/QCZTBUv7faQ/0.jpg)
Отбор корней по окружностиСкачать

Производная. Наибольшее и наименьшее значение тригонометрической функции. 10-11 классСкачать

№ 26704 Найдите наибольшее значение функции y=16tgx-16x+4π-5 на отрезке [-π/4; π/4].Скачать
![№ 26704 Найдите наибольшее значение функции y=16tgx-16x+4π-5 на отрезке [-π/4; π/4].](https://i.ytimg.com/vi/wMb3S9rLYrI/0.jpg)
Тригонометрическая окружность. Как выучить?Скачать