Содержание

Как нагрузочная прямая используется в проектировании схем
Анализ цепей с выпрямительными диодами, светодиодами и транзисторами
Создание нагрузочной прямой по вольт-амперной характеристике диода
Заключение
Ключ на биполярном транзисторе. Нагрузочная прямая.
Расчет ключа на биполярном транзисторе.
Контрольная работа. Выполним
Нагрузочные прямые постоянного и переменного тока
Радиотехнические устройства. Струтурные схемы
🎥 Видео

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Как нагрузочная прямая используется в проектировании схем

Из данной статьи из серии часто задаваемых инженерных вопросах (FEQ, Frequent Engineering Questions) вы узнаете, как использовать нагрузочную прямую при проектировании схем.

В этом учебном пособии будет описано, как нагрузочная прямая влияет на проектирование схемы, и как анализировать работу схемы, выбирая нагрузку по вольт-амперной характеристике.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Анализ цепей с выпрямительными диодами, светодиодами и транзисторами

Цепи, которые содержат нелинейные компоненты, такие как выпрямительные диоды, светодиоды или транзисторы, не могут быть всесторонне проанализированы с использованием методов, которые мы обычно применяем к цепям, состоящим только из резисторов, катушек индуктивности и конденсаторов.

Например, в следующей схеме мы не можем точно рассчитать напряжение на диоде, объединив два резистора в R_экв, и затем применив закон Ома.

Рисунок 1 – Пример диодной схемы

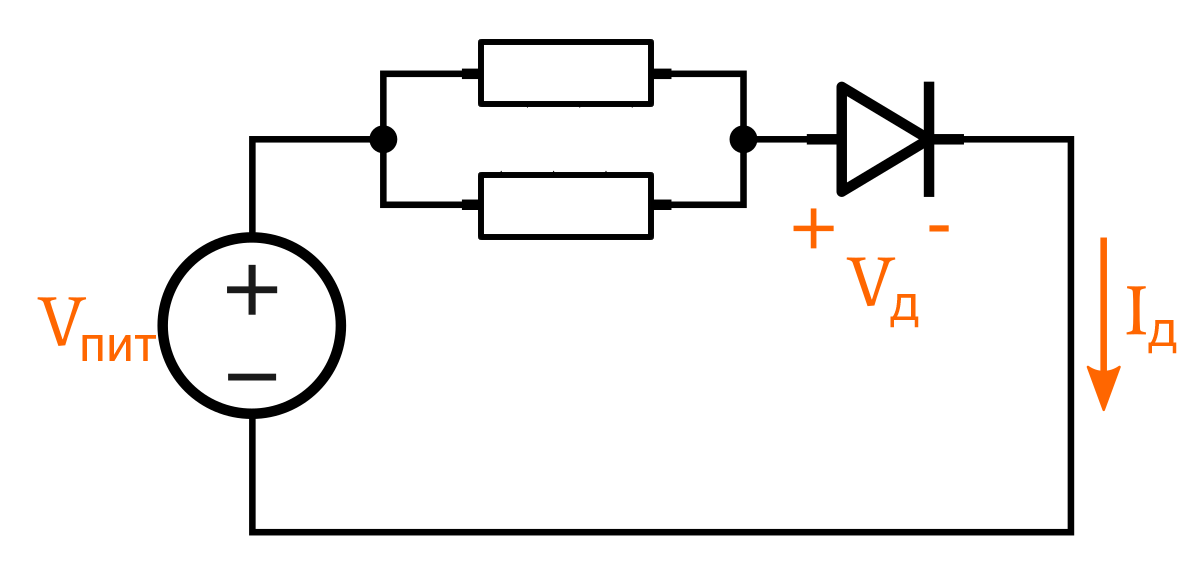
В таких случаях мы можем выполнить необходимый анализ, нарисовав диаграмму, состоящую из нагрузочной прямой и вольт-амперной характеристики нелинейного устройства.

Чтобы создать эту диаграмму, нам сначала нужно знать зависимость между током и напряжением нелинейного устройства. Эта информация может быть получена из технического описания устройства, или мы можем использовать кривые, которые представляют типовое поведение устройств, которые относятся к обобщенной категории, которая нас интересует, – например, стандартные кремниевые диоды или низковольтные NPN-транзисторы.

Затем мы создаем нагрузочную прямую на основе ограничений, налагаемых другими элементами схемы.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Создание нагрузочной прямой по вольт-амперной характеристике диода

В диодной схеме, показанной выше, мы знаем, что напряжение на диоде не может быть выше, чем напряжение питания V_пит. Мы также знаем, что ток через диод не может быть выше, чем V_пит/R_экв, потому что ток цепи ограничен этим значением резисторов; диод может оказывать дополнительное сопротивление току и, следовательно, создавать значение ниже, чем V_пит/R_экв, но он не может увеличить ток выше уровня, установленного резисторами.

Таким образом, мы имеем ограничение как для падения напряжения на диоде, так и для тока, протекающего через диод. Все точки, лежащие на прямой линии между этими двумя ограничениями, представляют все возможные комбинации тока и напряжения, которые возможны в ограничивающей обстановке, создаваемой линейными элементами цепи.

Рисунок 2 – График, показывающий пересечение нагрузочной прямой и ВАХ диода

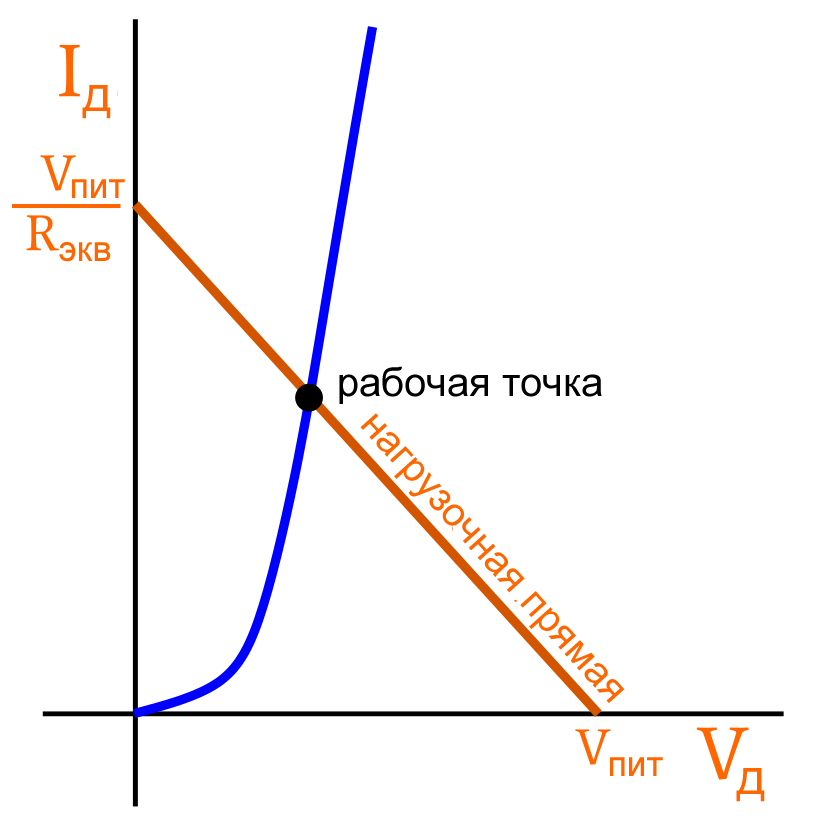
Эта прямая линия – это то, что мы называем нагрузочной прямой.

Только одна из этих точек соответствует сочетанию тока и напряжения, которое возможно при электрическом поведении диода, которое описывается «диодным уравнением». Мы находим эту точку, отмечая пересечение нагрузочной прямой и кривой вольт-амперной характеристики диода, как показано выше. Точка пересечения соответствует рабочей точке цепи.

Видео:Уравнение прямой на плоскостиСкачать

Заключение

Что вам нужно узнать о нагрузочных прямых? Поделитесь своими вопросами в комментариях ниже.

Видео:Построение нагрузочной прямой и определение рабочей токи на ВАХ НЭСкачать

Ключ на биполярном транзисторе. Нагрузочная прямая.

Приветствую всех снова на нашем сайте, сегодня продолжаем активно погружаться в нюансы работы транзисторов и переходим к практическому рассмотрению одной из схем — ключа на биполярном транзисторе.

Суть схемы довольно проста и заключается в том, что как и любой переключатель, транзистор должен находиться в одном из двух состояний — открытом (включенном) или закрытом (выключенном). То есть либо транзистор пропускает ток, либо не пропускает. Приступаем к детальному разбору.

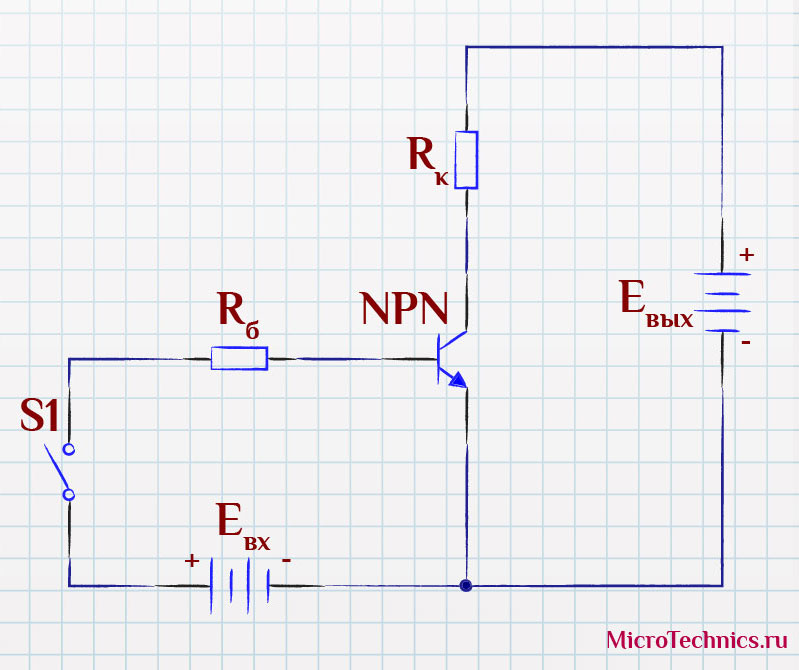
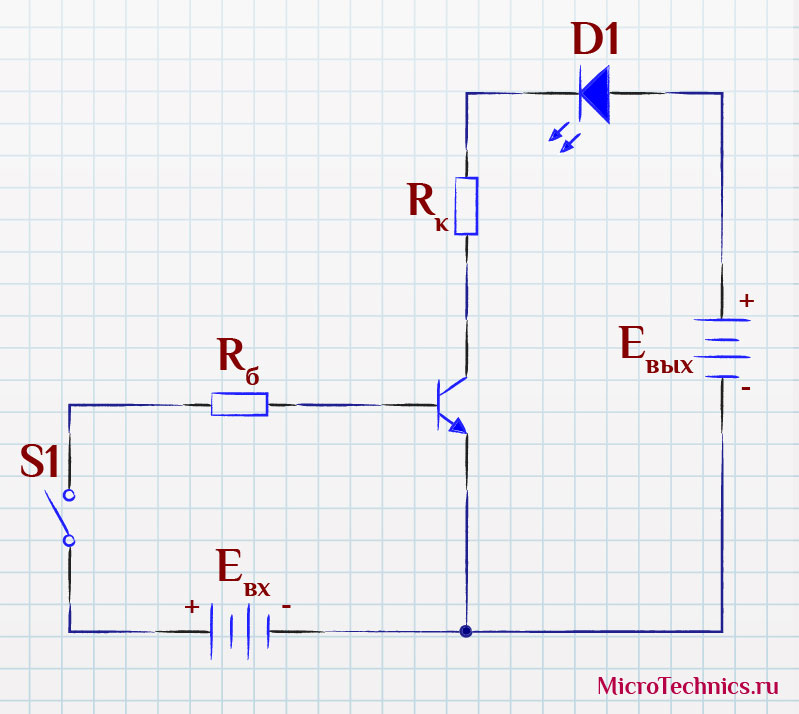
И первым делом рассмотрим непосредственно саму схему:

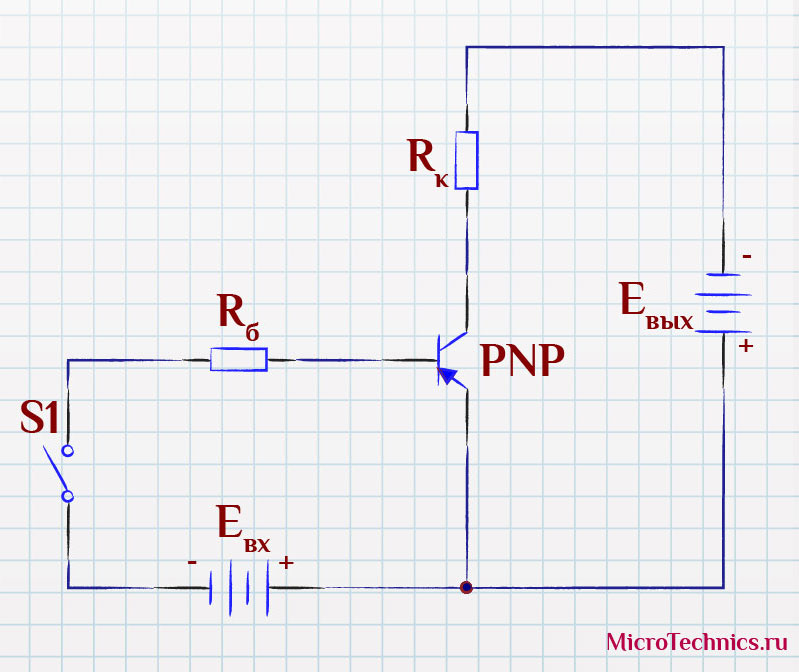
Здесь у нас используется n-p-n транзистор. А вот вариант для p-n-p:

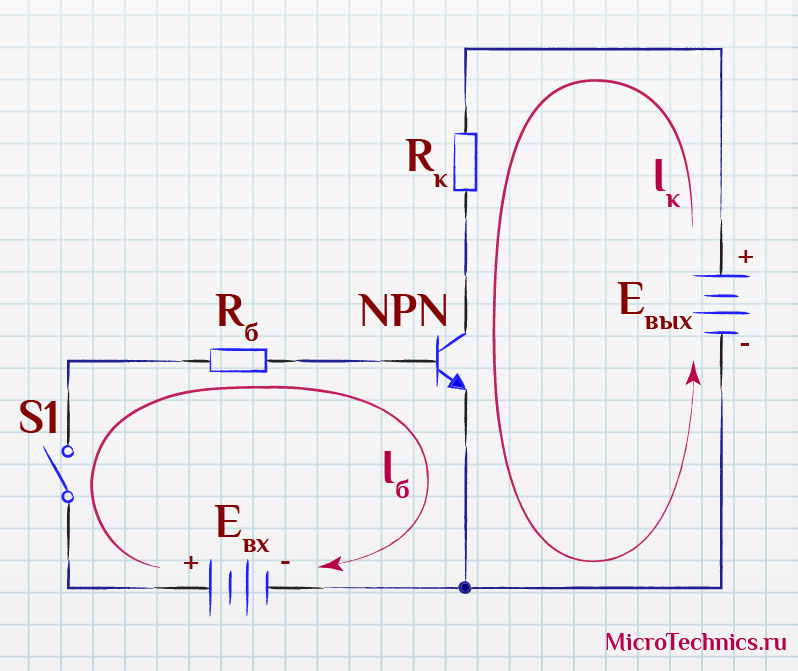
И по нашей уже устоявшейся традиции будем разбирать все аспекты работы на примере n-p-n транзистора. Суть и основные принципы остаются неизменными и для p-n-p. Так что работаем с этой схемой (здесь мы добавили протекающие по цепи токи):

Как вы уже заметили, схема очень напоминает включение транзистора с общим эмиттером. И действительно именно схема с ОЭ чаще всего используется при построении ключей. Только здесь у нас добавились два резистора ( R_б и R_к ). Вот с них и начнем.

Зачем нужен резистор в цепи базы?

Итак, нам нужно подать на переход база-эмиттер напряжение прямого смещения. Его величина указывается среди параметров конкретного транзистора и обычно составляет в районе 0.6 В. Также мы знаем, какой управляющий сигнал мы будем подавать на вход для того, чтобы открыть транзистор. Например, при использовании микроконтроллера (возьмем STM32 к примеру) для управления ключом, на входе цепи у нас будет либо 0 В (транзистор в данном случае закрыт), либо 3.3 В (транзистор открыт). В данной схеме сигнал на вход подается не с контроллера, а напрямую с источника напряжения E_ при замыкании переключателя S_1 .

Таким образом, получаем, что при 3.3 В на входе напряжение на резисторе R_б составит:

А теперь вспоминаем, что управление биполярным транзистором осуществляется изменением тока базы — а как его менять? Верно — изменяя сопротивление этого самого резистора. То есть, варьируя сопротивление резистора, мы меняем ток базы и, соответственно, этим самым вносим изменения в работу выходной цепи нашей схемы. Чуть позже мы рассмотрим практический пример для конкретных номиналов и величин и посмотрим на деле, как это работает.

Мы уже несколько раз использовали термины «транзистор открыт» и «закрыт». Понятно, что это означает наличие, либо отсутствие коллекторного тока, но давайте рассмотрим эти понятия применительно к режимам работы транзистора. И тут все достаточно просто:

для того, чтобы закрыть транзистор, мы стремимся перевести его в режим отсечки
а чтобы открыть — в режим насыщения

То есть при проектировании ключа на биполярном транзисторе мы преследуем цель переводить транзистор то в режим отсечки, то в режим насыщения в зависимости от управляющего сигнала на входе.

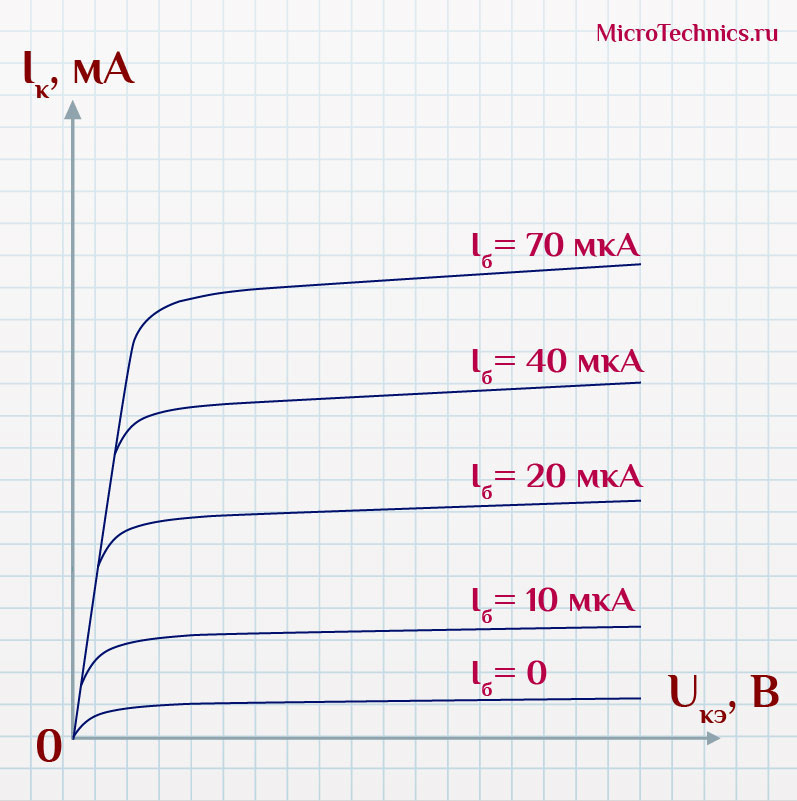
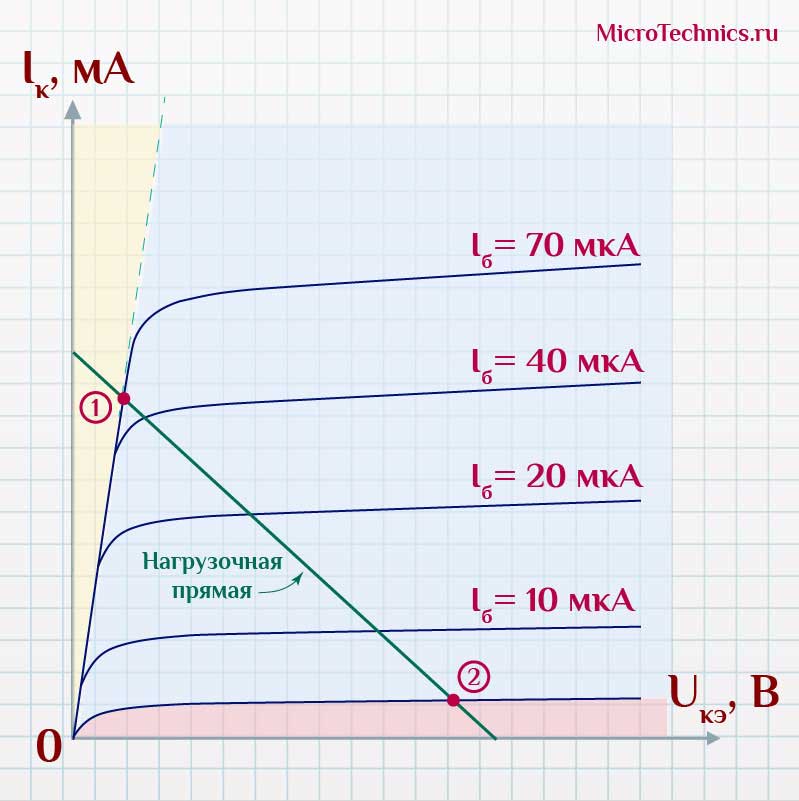
Переходим к рассмотрению коллекторной цепи разбираемой схемы. В данном резистор R_к выполняет роль нагрузки, а также ограничивает ток в цепи во избежания короткого замыкания источника питания E_ . И вот теперь пришло время вспомнить выходные характеристики, которые мы совсем недавно обсуждали:

Но в данном случае выходные параметры схемы определяются помимо всего прочего еще и нагрузкой (то есть резистором R_к ). Для коллекторной цепи мы можем записать:

Этим уравнением задается так называемая нагрузочная характеристика цепи. Поскольку резистор — линейный элемент ( U_R = I_R R ), то характеристика представляет из себя прямую (которую так и называют — нагрузочная прямая). Наносим ее на выходные характеристики транзистора и получаем следующее:

Рабочая точка в данной схеме будем перемещаться по нагрузочной прямой. То есть величины U_ и I_к могут принимать только те значения, которые соответствуют точкам пересечения выходной характеристики транзистора и нагрузочной прямой. Иначе быть не может.

И по итогу нам нужно обеспечить, чтобы в открытом состоянии рабочая точка оказалась в положении 1. В данном случае падение напряжения U_ на транзисторе будет минимальным, то есть почти вся полезная мощность от источника окажется на нагрузке. В закрытом же состоянии рабочая точка должна быть в положении 2. Тогда почти все напряжение упадет на транзисторе, а нагрузка будет выключена.

Теперь, когда мы разобрались с теоретическими аспектами работы ключа на транзисторе, давайте рассмотрим как же на практике производятся расчеты и выбор номиналов элементов.

Видео:§9 Уравнение прямой в отрезкахСкачать

Расчет ключа на биполярном транзисторе.

Добавим в схему полезную нагрузку в виде светодиода. Резистор R_к при этом остается на месте, он будет ограничивать ток через нагрузку и обеспечивать необходимый режим работы:

Пусть для включения светодиода нужно подать на него напряжение 3В ( U_д ). При этом диод будет потреблять ток, равный 50 мА ( I_д ). Зададим параметры транзистора (в реальных схемах эти значения берутся из документации на используемый транзистор):

Коэффициент усиления по току h_ = 100. 500 (всегда задан именно диапазон, а не конкретное значение)
Падение напряжения на переходе база-эмиттер, необходимое для открытия этого перехода: U_ = 0.6 medspace В .
Напряжение насыщения: U_ = 0.1 medspace В .

Мы берем конкретные значения для расчетов, но на практике все бывает несколько иначе. Как вы помните, параметры транзисторов зависят от многих факторов, в частности, от режима работы, а также от температуры. А температура окружающей среды, естественно, может меняться. Определить четкие значения из характеристик при этом бывает не так просто, поэтому нужно стараться обеспечить небольшой запас. К примеру, коэффициент усиления по току при расчете лучше принять равным минимальному из значений, приведенных в даташите. Если коэффициент в реальности будет больше, то это не нарушит работоспособности схемы, конечно, при этом КПД будет ниже, но тем не менее схема будет работать. А если взять максимальное значение h_ , то при определенных условиях может оказаться, что реальное значение оказалось меньше, и его уже недостаточно для обеспечения требуемого режима работы транзистора.

Итак, возвращаемся к примеру. Входными данными для расчета кроме прочего являются напряжения источников. В данном случае:

E_ = 3.3medspace В . Я выбрал типовое значение, которое встречается на практике при разработке схем на контроллерах. В этом примере подача и отключение этого напряжения осуществляется переключателем S_1 .
E_ = 9medspace В .

Первым делом нам необходимо рассчитать сопротивление резистора в цепи коллектора. Напряжения и ток выходной цепи во включенном состоянии связаны следующим образом:

При этом по закону Ома напряжение на резисторе R_ :

А ток у нас задан, поскольку мы знаем, какой ток потребляет нагрузка (в данном случае диод) во включенном состоянии. Тогда:

Итак, в этой формуле нам известно все, кроме сопротивления, которое и требуется определить:

Выбираем доступное значение сопротивления из стандартного ряда номиналов и получаем R_ = 120medspace Ом . Причем важно выбирать именно большее значение. Связано это с тем, что если мы берем значение чуть больше рассчитанного, то ток через нагрузку будет немного меньше. Это не приведет ни к каким сбоям в работе. Если же взять меньшее значение сопротивления, то это приведет к тому, что ток и напряжение на нагрузке будут превышать заданные, что уже хуже.

Пересчитаем величину коллекторного тока для выбранного значения сопротивления:

Пришло время определить ток базы, для этого используем минимальное значение коэффициента усиления:

А падение напряжения на резисторе R_б :

Теперь мы можем легко определить величину сопротивления:

Опять обращаемся к ряду допустимых номиналов. Но теперь нам нужно выбрать значение, меньшее рассчитанного. Если сопротивление резистора будет больше расчетного, то ток базы будет, напротив, меньше. А это может привести к тому, что транзистор откроется не до конца, и во включенном состоянии большая часть напряжения упадет на транзисторе ( U_ ), что, конечно, нежелательно.

Поэтому выбираем для резистора базы значение 5.1 КОм. И этот этап расчета был последним 👍 Давайте резюмируем, наши рассчитанные номиналы составили:

R_ = 5.1medspace КОм
R_ = 120medspace Ом

Кстати в схеме ключа на транзисторе обычно добавляют резистор между базой и эмиттером, номиналом, например, 10 КОм. Он нужен для подтяжки базы при отсутствии сигнала на входе. В нашем примере, когда S1 разомкнут, то вход просто висит в воздухе. И под воздействием наводок транзистор будет хаотично открываться и закрываться. Поэтому добавляется резистор подтяжки, чтобы при отсутствии входного сигнала потенциал базы был равен потенциалу эмиттера. В этом случае транзистор будет гарантированно закрыт.

Сегодня мы прошлись по классической схеме, которой я стараюсь придерживаться, то есть — от теории к практике. Надеюсь, что материал был понятен, а если возникнут какие-либо вопросы, пишите в комментарии, будем разбираться.

Видео:Составляем уравнение прямой по точкамСкачать

Контрольная работа. Выполним

Нагрузочные прямые постоянного и переменного тока

На выходных характеристиках транзистора точка покоя А , соответствующая выбранному значению тока базы, лежит на нагрузочной прямой постоянного тока (рис. 4.3). Её координаты обозначены как I 0 и U 0 . Нагрузочная прямая постоянного тока проходит через точку Е на оси абсцисс и точку Е / R К на оси ординат в соответствии с уравнением второго закона Кирхгофа для коллекторной цепи

E = U КЭ + R К I К .

(4.1)

Наклон нагрузочной прямой постоянного тока определяется сопротивлением выходной цепи постоянному току R = = R К . В общем случае оно включает все сопротивления, последовательно подключенные в выходной цепи транзистора к источнику питания.

Рис. 4.3 — Графическое представление работы каскада по постоянному и переменному току

Через разделительный конденсатор C 2 к коллектору подключена нагрузка R н , в которую передается часть переменной составляющей коллекторного тока. Другая часть ответвляется в резистор R К ( i к ( t ) = i н ( t ) + i R ( t ) ) . Следовательно, для переменной составляющей коллекторного тока резисторы R К и R н соединены параллельно. Их параллельное соединение называют сопротивлением выходной цепи переменному току:

= R К ‖ R н .(4.2)

При передаче сигнала мгновенные значения тока и напряжения в коллекторной цепи транзистора определяются соотношениями

I К = I 0 + i К ( t ) ;

(4.3)

U КЭ = U 0 + u вых ( t ) ,

(4.4)

причем переменные составляющие связаны уравнением

u вых ( t ) = − R

i К ( t ) .

(4.5)

Знак минус подчеркивает тот факт, что с ростом коллекторного тока напряжение на транзисторе (вследствие увеличения падения напряжения на резисторе RК ) уменьшается. Знак минус говорит о свойстве каскада с общим эмиттером инвертировать фазу входного сигнала при усилении.

Подставив в уравнение (4.5) значения переменных составляющих коллекторного тока и напряжения из (4.3) и (4.4), получим уравнение нагрузочной прямой переменного тока

U КЭ − U 0 = − R

( I К − I 0 ) .

(4.6)

Она проходит через точку покоя A ( I 0 , U 0 ) и точку на оси абсцисс с координатой U КЭ = U 0 + I 0 R

. По ней совершает колебания рабочая точка под действием сигнала, причем A ′ и A ″ определяют амплитуды переменных составляющих i К ( t ) и u вых ( t ) для заданной амплитуды изменения базового тока i Б ( t ) .

Путем рассмотренных графических построений легко определяется коэффициент усиления по напряжению при работе каскада в режиме большого сигнала.