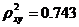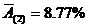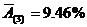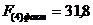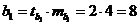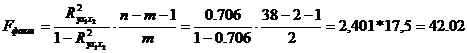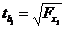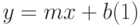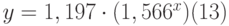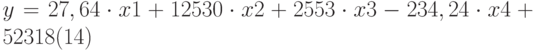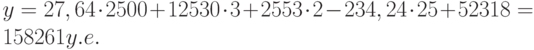С помощью метода наименьших квадратов мы получили лишь оценки параметров уравнения регрессии. Чтобы оценить надежность модели необходимо проверить, значимы ли ее параметры (т.е. значимо ли они отличаются от нуля в «истинном» уравнении регрессии – регрессии, построенной для генеральной совокупности). При этом используют статистические методы проверки гипотез. С помощью статистических методов проверки гипотез можно также проверить значимость коэффициента парной линейной корреляции, а также значимость коэффициента множественной корреляции (т.е. проверить значимо ли они отличаются от нуля в генеральной совокупности.
В качестве основной гипотезы (Н0) выдвигают гипотезу о незначимом отличии от нуля «истинного» параметра регрессии или коэффициента корреляции. Альтернативной гипотезой (Н1), при этом является гипотеза обратная, т.е. о неравенстве нулю «истинного» параметра или коэффициента корреляции. Мы заинтересованы в том, чтобы основная гипотеза была отвергнута. Для проверки этой гипотезы используется t-статистика критерия проверки гипотезы, имеющая распределение Стьюдента.
Найденное по данным наблюдений значение t-статистики (его еще называют наблюдаемым или фактическим) сравнивается с критическим значением t-статистики, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Критическое значение определяется в зависимости от уровня значимости (a) и числа степеней свободы, которое равно (n-h), n-число наблюдений, h – число оцениваемых параметров в уравнении регрессии. В случае линейной парной регрессии h=2, а число степеней свободы равно (n-2).
Если фактическое значение t-статистики взятое по модулю больше критического, то основную гипотезу отвергают и считают, что с вероятностью (1-a) «истинной» параметр регрессии (либо коэффициент корреляции) значимо отличается от нуля.
Если фактическое значение t-статистики меньше критического (по модулю), то нет оснований отвергать основную гипотезу, т.е. «истинной» параметр регрессии (либо коэффициент корреляции) незначимо отличается от нуля при уровне значимости a.
Для анализа статистической значимости полученных коэффициентов необходимо проверить гипотезу Н0: b г j=0 (при альтернативной Н1: b г j≠0). Статистика критерия проверки рассчитывается по формуле: 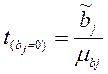
где bj — оценка коэффициента регрессии b1, полученная по наблюдаемым данным;
mbj – стандартная ошибка оценки коэффициента регрессии bj (корень из дисперсии оценки коэффициента регрессии – μ 2 [bj]; берется из оценки матрицы ковариаций 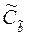
В случае парной линейной регрессии 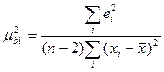
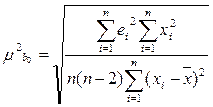
Сумму квадратов отклонений фактических значений результата от смоделированных — 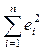
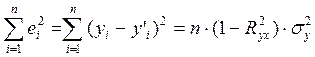
Если (п-т-1), то есть число степеней свободы, достаточно велико (не менее 8 — 10), то при 5%-ном уровне значимости и двусторонней альтернативной гипотезе критическое значение t-статистики приблизительно равно двум. Здесь, как и в случае парной регрессии, можно приближенно считать оценку незначимой, если t-статистика по модулю меньше единицы, и весьма надежной, если модуль t-статистики больше трех. Другие критерии качества полученного уравнения регрессии будут рассмотрены ниже.
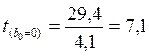
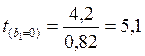
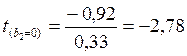
Так как │tнабл│>tкр (для всех параметров), то все параметры можно признать значимыми.
Для проверки гипотезы о незначимом отличии от нуля «истинного» коэффициента линейной парной корреляции: ryx г =0 (рассчитанного для генеральной совокупности) используют статистику критерия:
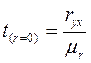
Для линейного парного уравнения регрессии:
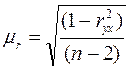
В парной линейной регрессии между наблюдаемыми значениями статистик критериев существует взаимосвязь: t (b1=0)=t(r=0).
Оценка значимости уравнения множественной регрессии в целом осуществляется путем проверки основной гипотезы Н0: R 2 г y(x1. xm)=0 или δ* 2 ≤ε* 2 (гипотеза о статистической незначимости уравнения регрессии). При этом альтернативная гипотеза — Н1: R 2 г y(x1. xm)¹0 или δ* 2 >ε* 2 (гипотеза о статистической значимости уравнения регрессии).
Для проверки основной гипотезы используют статистику, рассчитываемую по следующей формуле: 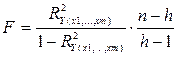
Данная статистика имеет F-распределение (Фишера-Снедоккора). Поэтому для поиска критического значения — Fкр пользуются таблицами распределения Фишера-Снедоккора, задаваясь при этом уровнем значимости a (обычно его берут равным 0,05) и двумя числами степеней свободы k1=h-1 и k2=n-h.
Сравнивая фактическое значение F-статистики критерия, вычисленное по данным наблюдений — (Fнабл) с критическим — Fкр(a;k1;k2). Если Fнабл Fкр(a;k1;k2), то основную гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии. Для уверенных выводов отличие наблюдаемого и критического значений F-критерия должно быть по крайней мере в 4 раза.
! В случае линейной парной регрессии имеет место следующая взаимосвязь статистик: : 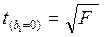
Для нашего примера:
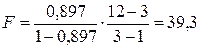
Оценка значимости дополнительного включения фактора (частный F–критерий).Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличить долю объясненной вариации результативного признака. Это может быть связано с последовательностью вводимых факторов (т.к. существует корреляция между самими факторами).
Мерой оценки значимости улучшения качества модели, после включения в нее фактора хj, служит частный F-критерий — Fxj:
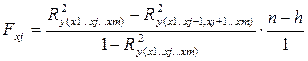
В числителе – прирост доли вариации y за счет дополнительно включенного в модель фактора xj.
Допустим, что оценивается значимость фактора х1, как дополнительно включенного в модель y=f(x2). Тогда частный F-критерий будет вычисляться по формуле:
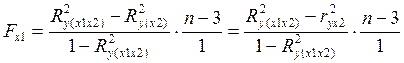
Частный F-критерий оценивает значимость коэффициентов «чистой» регрессии (bj). Существует взаимосвязь между частным F–критерием — Fxj и t-критерием, используемым для оценки значимости коэффициента множественной регрессии при j–ом факторе: 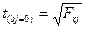
Для нашего примера:
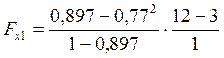
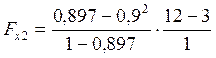
- Надежность уравнения регрессии чем ниже тем
- Пример нахождения статистической значимости коэффициентов регрессии
- Оценим статистическую надежность результатов регрессионного моделирования.
- Прогнозирование. Регрессионный анализ, его реализация и прогнозирование
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Сущность метода регрессионного анализа
- Линейная регрессия
- Нелинейная регрессия
- Множественная регрессия
- Использование функций регрессии
- Правила ввода функций
- Линия тренда
- Простая линейная регрессия
- Экспоненциальная регрессия
- Множественная линейная регрессия
- ЗАДАНИЕ
- 📺 Видео
Видео:Линейная регрессияСкачать

Надежность уравнения регрессии чем ниже тем
С помощью метода наименьших квадратов мы получили лишь оценки параметров уравнения регрессии. Чтобы оценить надежность модели необходимо проверить, значимы ли ее параметры (т.е. значимо ли они отличаются от нуля в «истинном» уравнении регрессии – регрессии, построенной для генеральной совокупности). При этом используют статистические методы проверки гипотез. С помощью статистических методов проверки гипотез можно также проверить значимость коэффициента парной линейной корреляции, а также значимость коэффициента множественной корреляции (т.е. проверить значимо ли они отличаются от нуля в генеральной совокупности.
В качестве основной гипотезы (Н0) выдвигают гипотезу о незначимом отличии от нуля «истинного» параметра регрессии или коэффициента корреляции. Альтернативной гипотезой (Н1), при этом является гипотеза обратная, т.е. о неравенстве нулю «истинного» параметра или коэффициента корреляции. Мы заинтересованы в том, чтобы основная гипотеза была отвергнута. Для проверки этой гипотезы используется t-статистика критерия проверки гипотезы, имеющая распределение Стьюдента.
Найденное по данным наблюдений значение t-статистики (его еще называют наблюдаемым или фактическим) сравнивается с критическим значением t-статистики, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Критическое значение определяется в зависимости от уровня значимости (a) и числа степеней свободы, которое равно (n-h), n-число наблюдений, h – число оцениваемых параметров в уравнении регрессии. В случае линейной парной регрессии h=2, а число степеней свободы равно (n-2).
Если фактическое значение t-статистики взятое по модулю больше критического, то основную гипотезу отвергают и считают, что с вероятностью (1-a) «истинной» параметр регрессии (либо коэффициент корреляции) значимо отличается от нуля.
Если фактическое значение t-статистики меньше критического (по модулю), то нет оснований отвергать основную гипотезу, т.е. «истинной» параметр регрессии (либо коэффициент корреляции) незначимо отличается от нуля при уровне значимости a.
Для анализа статистической значимости полученных коэффициентов необходимо проверить гипотезу Н0: b г j=0 (при альтернативной Н1: b г j≠0). Статистика критерия проверки рассчитывается по формуле: 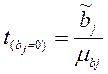
mbj – стандартная ошибка оценки коэффициента регрессии bj (корень из дисперсии оценки коэффициента регрессии – μ 2 [bj]; берется из оценки матрицы ковариаций 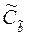
В случае парной линейной регрессии 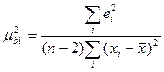
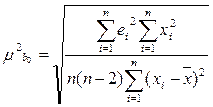
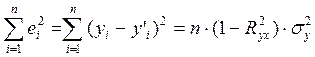
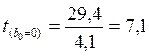
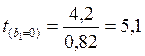
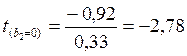
Так как │tнабл│>tкр (для всех параметров), то все параметры можно признать значимыми.
Для проверки гипотезы о незначимом отличии от нуля «истинного» коэффициента линейной парной корреляции: ryx г =0 (рассчитанного для генеральной совокупности) используют статистику критерия:
Для линейного парного уравнения регрессии:
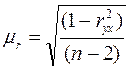
В парной линейной регрессии между наблюдаемыми значениями статистик критериев существует взаимосвязь: t (b1=0)=t(r=0).
! В случае линейной парной регрессии имеет место следующая взаимосвязь статистик: : 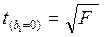
Для нашего примера:
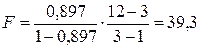
Оценка значимости дополнительного включения фактора (частный F–критерий).Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличить долю объясненной вариации результативного признака. Это может быть связано с последовательностью вводимых факторов (т.к. существует корреляция между самими факторами).
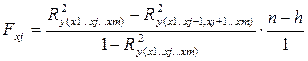
В числителе – прирост доли вариации y за счет дополнительно включенного в модель фактора xj.
Допустим, что оценивается значимость фактора х1, как дополнительно включенного в модель y=f(x2). Тогда частный F-критерий будет вычисляться по формуле:
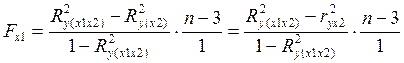
Для нашего примера:
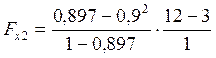
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Пример нахождения статистической значимости коэффициентов регрессии
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Оценим статистическую надежность результатов регрессионного моделирования.


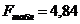
Вывод: 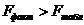
VI. Теперь по значениям характеристики выберем лучшее уравнение регрессии. Для этого составим таблицу.
| Уравнение |  |  |  |  |
| Линейное | 0,8313 | 0,8355 | 9,0930 | 24,61 |
| Степенное | 0,8319 | 0,9305 | 8,7684 | 24,73 |
| Показательное | 0,7993 | 0,8588 | 9,4552 | 19,39 |
| Равн. гипербола | 0,8622 | 0,8149 | 7,9197 | 31,80 |
| max | min | max |
Так как 
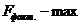
VII. Рассчитаем прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определим доверительный интервал прогноза для уровня значимости 
Если прогнозное значение фактора увеличится на 7%, то прогнозное значение среднемесячной заработной платы составит 107% от ее среднего уровня:
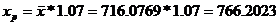
Тогда прогнозное значение потребительских расходов составит:

Средняя ошибка прогнозируемого значения вычисляется по формуле:

Предельную ошибку прогноза найдем по формуле:
Значение 

Доверительный интервал прогноза:
Если прогнозировать увеличение среднемесячной зарплаты на 7% от ее среднего уровня, то можно прогнозировать потребительские расходы на душу населения в среднем 434,4284 тыс. руб., которые колеблются от 344,1346 тыс. руб. до 524,7222 тыс. руб. с надежностью 0,95. Выполненный прогноз потребительских расходов удовлетворительный, так как диапазон верхней и нижней границ доверительного интервала составляет 1,52 раза:
Ответ:
1) y = 65.9264 + 0.4675*x – уравнение линейной регрессии
2) 
3) 
4) 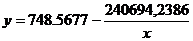
Показатели корреляции и детерминации:
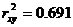


Средний коэффициент эластичности:

Средняя ошибка аппроксимации:


Прогнозное значение результата:

Доверительный интервал прогноза:
(344,1346; 524,7222) тыс. руб.
Задача №2.
По 38 предприятиям одной отрасли исследовалась зависимость производительности труда – y от уровня квалификации рабочих – x1 bи энерговооруженности их труда – x2. Результаты оказались следующими:
Задание:
1. Определите параметр b1 и заполните пропущенные значения.
2. Оцените значимость уравнения в целом, используя значение множественного коэффициента корреляции.
3. Какой из факторов оказывает более сильное воздействие на результат?
Решение:
1. Есть уравнение регрессии: Y = 3 + b1x1 + 4 x2, m – средние стандартные ошибки.



2. Множественный коэффициент корреляции 
Коэффициент детерминации R 2 = 0,84 2 =0.7056.
Вариация результата y на 70,6% объясняется вариацией факторов x1 и x2., а остальные 29,4% объясняются другими факторами, не учтёнными в данном уравнении регрессии. Коэффициент детерминации равен 0,706; связь очень тесная.
Для оценки значимости уравнения в целом находим общий F – критерий Фишера.

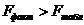
3. Найдем частные F –критерии Фишера по формуле


Ответ:
2. Параметры уравнения регрессии статистически значимы.
3. 
Видео:Математика #1 | Корреляция и регрессияСкачать

Прогнозирование. Регрессионный анализ, его реализация и прогнозирование
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Сущность метода регрессионного анализа
Одним из методов, используемых для прогнозирования, является регрессионный анализ.
Регрессия – это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей.
На графике данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным.
Линейная регрессия
Линейная регрессия дает возможность наилучшим образом провести прямую линию через точки одномерного массива данных (рис.13.1 а). Уравнение с одной независимой переменной, описывающее прямую линию, имеет вид:
где:x – независимая переменная;
y – зависимая переменная;
m – характеристика наклона прямой;
b – точка пересечения прямой с осью у.
Например, имея данные о реализации товаров за год с помощью линейной регрессии можно получить коэффициенты прямой (1) и, предполагая дальнейший линейный рост, получить прогноз реализации на следующий год.
Нелинейная регрессия
Нелинейная регрессия позволяет подбирать к табличным данным нелинейное уравнение (рис. 13.1 рис. 13.1, б.) – параболу, гиперболу и др. Excel реализует нелинейность в виде экспоненты, т.е. подбирает кривую вида:
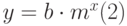
которая позволяет наилучшим образом провести экспоненциальную кривую по точкам данных, которые изменяются нелинейно.
Так, например, данные о росте населения почти всегда лучше описываются не прямой линией, а экспоненциальной кривой. При этом нужно помнить, что достоверное прогнозирование возможно только на участках подъёма или спуска кривой (при отрицательных значениях х), т.к. сама кривая (2) изменяется монотонно, без точек перегиба. Например, делать экспоненциальный прогноз для функции, изменяющейся синусоидально, можно только на участках подъёма или спуска функции, для чего её разбивают на соответствующие интервалы.
Множественная регрессия
Множественная регрессия представляет собой анализ более одного набора данных аргумента х и даёт более реалистичные результаты.
Множественный регрессионный анализ также может быть как линейным, так и экспоненциальным. Уравнение регрессии (1) и (2) примут соответственно вид (3) и (4):
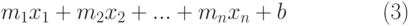 | ( 3) |
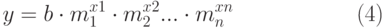 | ( 4) |
С помощью множественной регрессии, например, можно оценить стоимость дома в некотором районе, основываясь на данных его площади, размерах участка земли, этажности, вида из окон и т.д.
Использование функций регрессии
В Excel имеется 5 функций для линейной регрессии: ЛИНЕЙН(…)(LINEST), ТЕНДЕНЦИЯ(…), ПРЕДСКАЗ(…), НАКЛОН(…), СТОШУХ(…)) и 2 функции для экспоненциальной регрессии – ЛГРФПРИБЛ(…) и РОСТ(…).
Рассмотрим некоторые из них.
Функция ЛИНЕЙН((LINEST) вычисляет коэффициент m и постоянную b для уравнения прямой (1). Синтаксис функции:
Известные_значения_у и известные_значения_х – это множество значений у и необязательное множество значений х (их вводить необязательно), которые уже известны для соотношения (1).
Константа – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
Статистика – это логическое значение, которое указывает требуется ли вывести дополнительную статистику по регрессии.
| mn | mn-1 | … | m2 | m1 | b |
|---|---|---|---|---|---|
| sen | sen-1 | … | se2 | se1 | seb |
| r 2 | sey | … | #Н/Д | #Н/Д | #Н/Д |
| F | df | … | #Н/Д | #Н/Д | #Н/Д |
| ssreg | ssresid | … | #Н/Д | #Н/Д | #Н/Д |
seb – стандартное значение ошибки для постоянной b (seb равно #Н/Д, т.е. «нет допустимого значения», если конст. имеет значение ЛОЖЬ);
r 2 – коэффициент детерминированности. Сравниваются фактические значения у и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями у. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений у;
sey – стандартная ошибка для оценки у (предельное отклонение для у);
F – F-cтатистика, или F-наблюдаемое значение. Она используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;
df – степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надёжности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН;
ssreg – регрессионная сумма квадратов;
ssresid – остаточная сумма квадратов;
#Н/Д – ошибка, означающая «нет доступного значения».
Любую прямую можно задать её наклоном m и у-пересечением:
Если для функции у имеется только одна независимая переменная х, можно получить наклон и у-пересечение непосредственно, используя следующие формулы:
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точными являются модель, используемая функцией ЛИНЕЙН, и значения, получаемые из уравнения прямой.
В случае экспоненциальной регрессии аналогом функции (5) является функция ЛГРФПРИБЛ(LOGEST):
которая отличается лишь тем, что вычисляет коэффициенты m и b для экспоненциальной кривой (2).
Функция ТЕНДЕНЦИЯ(TREND) имеет вид:
возвращает числовые значения, лежащие на прямой линии, наилучшим образом аппроксимирующие известные табличные данные.
Новые_значения_х – это те, для которых необходимо вычислить соответствующие значения у.
Если параметр новые_значения_х пропущен, то считается, что он совпадает с известными х. Назначение остальных параметров функции ТЕНДЕНЦИЯ совпадает с описанными выше.
В случае экспоненциальной регрессии аналогом функции (7) является функция РОСТ(GROWTH):
возвращает стандартную погрешность регрессии – меру погрешности предсказываемого значения у для заданного значения х.
Правила ввода функций
Формулы(5)-(8) являются табличными, т.е. они заменяют собой несколько обычных формул и возвращают не один результат, а массив результатов. Поэтому необходимо соблюдать следующие правила:
Линия тренда
Excel позволяет наглядно отображать тенденцию данных с помощью линии тренда, которая представляет собой интерполяционную кривую, описывающую отложенные на диаграмме данные.
Для того, чтобы дополнить диаграмму исходных данных линией тренда, необходимо выполнить следующие действия:
Чтобы отобразить на графике (гистограмме и др.) новые, прогнозируемые в результате регрессионного анализа данные, нужно:
На диаграмме появится продолжение кривой, построенной по новым данным.
Простая линейная регрессия
Пример 1. Функция ТЕНДЕНЦИЯ(TREND)
а) Предположим, что фирма может приобрести земельный участок в июле. Фирма собирает информацию о ценах за последние 12 месяцев, начиная с марта, на типичный земельный участок. Название первого столбца «Месяц» с данными о номерах месяцев записано в ячейке А1, а второго столбца «Цена» – в ячейке В1. Номера месяцев с 1 по 12 (известные значения х) записаны в ячейки А2…А13. Известные значения у содержат множество известных значений (133 890 руб., 135 000 руб., 135 790 руб., 137 300 руб., 138 130 руб., 139 100 руб., 139 900 руб., 141 120 руб., 141 890 руб., 143 230 руб., 144 000 руб., 145 290 руб.), которые находятся в ячейках В2;В13 соответственно (данные условия). Новые значения х, т.е. числа 13, 14,15,16,17 введём в ячейки А14…А18. Для того чтобы определить ожидаемые значения цен на март, апрель, май, июнь, июль, выделим любой интервал ячеек, например, B14:B18 (по одной ячейке для каждого месяца) и в строке формул введем функцию:
После нажатия клавиш Ctrl+ Shift+Enter данная функция будет выделена как формула вертикального массива, а в ячейках B14:B18 появится результат: .
Таким образом, в июле фирма может ожидать цену около 150 244 руб.
б) Тот же результат будет получен, если вводить в формулу не все массивы переменных х и у, а использовать часть массивов, которые предусматриваются автоматически по умолчанию. Тогда формула (10) примет вид:
В формуле (11) используется массив по умолчанию (1:2:3:4:5:6:7:8:9:10:11:12) для аргумента «известные_значения_х», соответствующий 12 месяцам, для которых имеются данные по продажам. Он должен был бы быть помещен в формуле (11) между двумя знаками ;;. Массив (13:14:15:16:17) соответствует следующим 5 месяцам, для которых и получен массив результатов (146172:147190:148208:149226:150244).
Элементы массивов разделяет знак «:», который указывает на то, что они расположены по столбцам.
в) Аргумент «новые значения х» можно задать другим массивом ячеек, например, В14:В18, в которые предварительно записаны те же номера месяцев 13,14,15,16,17. Тогда вводимая в строку формул функция примет вид =ТЕНДЕНЦИЯ(В2:В13;;В14:В18).
Пример 2. Функция ЛИНЕЙН
а) Дана таблица изменения температуры в течение шести часов, введённая в ячейки D2 :E7 (табл. 13.2 таблица 13.2).
Требуется определить температуру во время восьмого часа.
Выделим ячейки D8:E12 для вывода результата, введем в строку ввода формулу =ЛИНЕЙН(Е2:Е7;D2:D7;1;1), нажмем клавиши Сtrl+Shift+Enter, в выделенных ячейках появится результат:
| 3,142857 | -3,3333333 |
| 0,540848 | 2,106302 |
| 0,894088 | 2,2625312 |
| 33,76744 | 4 |
| 172,8571 | 20,47619 |
Таким образом, коэффициент m=3,143 со стандартной ошибкой 0,541, а свободный член b=-3,333 со стандартной ошибкой 2,106, т.е. функция, описывающая данные табл. 13.2 таблица 13.2, имеет вид
Стандартные ошибки показывают максимально возможное отклонение параметра от рассчитанной величины. Для у оно составляет 2,263, т.е. реальное значение у может лежать в пределах 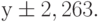
Точность приближения к табличным данным (коэффициент детерминированности r 2 ) составляет 0,894 или 89,4%, что является высоким показателем. При х=8 получим: у=3,143*8-3,333=21,81 град.
б) Тот же результат можно получить, использовав функцию =ТЕНДЕНЦИЯ(Е2:Е7;;G2:G5) для, например, следующих четырёх часов, предварительно введя в ячейки G2 :G5 числа с 7 до 10. Выделив ячейки Н2:Н5, введя в строку формул эту функцию и нажав Сtrl+Shift+Enter, получим в выделенных ячейках массив , т.е. для восьмого часа значение 
в) Функция ПРЕДСКАЗ ( FORECAST ) – позволяет предсказать значение у для нового значения х по известным значениям х и у, используя линейное приближение зависимости у=f(x).
Для данных примера 2 ввод формулы =ПРЕДСКАЗ(8;Е2:Е7;D2:D7) выводит в заранее выделенной ячейке результат 21,809. Новое значение х может быть задано не числом, а ячейкой, в которую записано это число.
Отличие функции ПРЕДСКАЗ от функции ТЕНДЕНЦИЯ заключается в том, что ПРЕДСКАЗ прогнозирует значения функции линейного приближения только для одного нового значения х.
Экспоненциальная регрессия
Пример 3
а) Функция ЛГРФПРИБЛ.
Рассмотрим условие примера 2.
| 1,56628015 | 1,196513 |
| 0,02038299 | 0,07938 |
| 0,99181334 | 0,085268 |
| 484,599687 | 4 |
| 3,52335921 | 0,029083 |
Таким образом, коэффициент m=1,566, а b=1,197, т.е. уравнение приближающей кривой имеет вид:
Поскольку интерполяция табл. 13.2 таблица 13.2 экспоненциальной кривой даёт более точное приближение (99,2%) и с меньшими стандартными ошибками для m, b и у, в качестве приближающего уравнения принимаем уравнение (13).
При х=8 получим у=1,197*34,363=41,131 град.
б) Функция РОСТ вычисляет прогнозируемое по экспоненциальному приближению значение у для новых значений х, имеет формат:
Примечание. При выборе экспоненциальной приближающей кривой следует учитывать, что интерполировать ею можно только участки, где функция монотонно возрастает или убывает (при отрицательном аргументе х), т.е. функцию, имеющую точки перегиба (например, параболу, синусоиду, кривую рис. 2 – т. А и др.) следует разбить на участки монотонного изменения от одной точки перегиба до другой и каждый участок интерполировать отдельно. Для рисунка 2 функцию нужно разбить на 2 участка – от начала до т. А и от т. А до конца кривой.
Множественная линейная регрессия
Пример 4
Предположим, что коммерческий агент рассматривает возможность закупки небольших зданий под офисы в традиционном деловом районе. Агент может использовать множественный регрессионный анализ для оценки цены здания под офис на основе следующих переменных:
у – оценочная цена здания под офис;
х1 – общая площадь в квадратных метрах;
х2 – количество офисов;
х3 – количество входов;
х4 – время эксплуатации здания в годах.
Агент наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные:
| А | В | С | D | Е | |
|---|---|---|---|---|---|
| 1 | х1— площадь, м2 | х2 – офисы | х3 – входы | х4 – срок, лет | у – цена, у.е. |
| 2 | 2310 | 2 | 2 | 20 | 42000 |
| 3 | 2333 | 2 | 2 | 12 | 144000 |
| 4 | 2356 | 3 | 1,5 | 33 | 151000 |
| 5 | 2379 | 3 | 2 | 43 | 151000 |
| 6 | 2402 | 2 | 3 | 53 | 139000 |
| 7 | 2425 | 4 | 3 | 23 | 169000 |
| 8 | 2448 | 2 | 1,5 | 99 | 126000 |
| 9 | 2471 | 2 | 2 | 34 | 142000 |
| 10 | 2494 | 3 | 3 | 23 | 163000 |
| 11 | 2517 | 4 | 4 | 55 | 169000 |
| 12 | 2540 | 2 | 3 | 22 | 149000 |
«Пол-входа» означает вход только для доставки корреспонденции.
В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (х1,х2,х3,х4) и зависимой переменной (у), т.е. ценой зданий под офис в данном районе.
| А | В | С | D | E | |
|---|---|---|---|---|---|
| 14 | -234,237 | 2553,210 | 12529,7682 | 27,6413 | 52317,83 |
| 15 | 13,2680 | 530,6691 | 400,066838 | 5,42937 | 12237,36 |
| 16 | 0,99674 | 970,5784 | #Н/Д | #Н/Д | #Н/Д |
| 17 | 459,753 | 6 | #Н/Д | #Н/Д | #Н/Д |
| 18 | 1732393319 | 5652135 | #Н/Д | #Н/Д | #Н/Д |
Уравнение множественной регрессии 
Это значение может быть вычислено с помощью функции ТЕНДЕНЦИЯ:
При интерполяции с помощью функции
для получения уравнения множественной экспоненциальной регрессии выводится результат:
| 0,99835752 | 1,0173792 | 1,0830186 | 1,0001704 | 81510,335 |
| 0,00014837 | 0,0065041 | 0,0048724 | 6,033Е-05 | 0,1365601 |
| 0,99158875 | 0,0105158 | #Н/Д | #Н/Д | #Н/Д |
| 176,832548 | 6 | #Н/Д | #Н/Д | #Н/Д |
| 0,07821851 | 0,0006635 | #Н/Д | #Н/Д | #Н/Д |
| #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д |
Коэффициент детерминированности здесь составляет 0,992 (99,2%), т.е. меньше, чем при линейной интерполяции, поэтому в качестве основного следует оставить уравнение множественной регрессии (14).
Таким образом, функции ЛИНЕЙН, ЛГРФПРИБЛ, НАКЛОН определяют коэффициенты, свободные члены и статистические параметры для уравнений одномерной и множественной регрессии, а функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ, РОСТ позволяют получить прогноз новых значений без составления уравнения регрессии по значениям тренда.
ЗАДАНИЕ
Вариант задания к данной лабораторной работе включает две задачи. Для каждой из них необходимо составить и определить:
Варианты заданий (номер варианта соответствует номеру компьютера).
Для выполнения задания нужно ввести ряд из 12 ячеек с ценами конкурирующей фирмы, сделать прогноз цены на следующий месяц и др. (см. Задание).
Для выполнения задания нужно составить таблицу со столбцами вида:
и сделать множественный регрессионный прогноз (см. Задание).
Для выполнения задания нужно составить таблицу вида:
| Годы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| х1-хлеб, кг | 23,5 | 26,7 | 27,9 | 30,1 | 31,5 | 35,7 | 38,3 | 40,1 | 41,5 | 42,8 | |
| х2-молоко, л | 20,45 | 22 | 23,8 | 25,9 | 27,4 | 29 | 33,5 | 36,8 | 38,1 | 39,5 | |
| У-доход, р. | 6600 | 7200 | 8400 | 10500 | 12750 | 14730 | 16240 | 17000 | 18050 | 18250 |
и получить два уравнения – у=f(x1) и у=f(x2), сделать прогноз на следующий год для рядов х1, х2, у и др. (см. Задание).
Исходные данные нужно ввести в таблицу вида:
| А | В | С | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | х1-эрудиция | х2-энергичность | х3-люди | х4-внешность | х5-знания | Эффективность | |
| 2 | Агент 1 | 0,8 | 0,2 | 0,4 | 0,6 | 1,0 | 76% |
| 3 | Агент 2 | 0,74 | 0,3 | 0,39 | 0,58 | 0,95 | 78% |
| 4 | Агент 3 | 0,67 | 0,41 | 0,35 | 0,5 | 0,83 | 79% |
| 5 | Агент 6 | 0,59 | 0,59 | 0,33 | 0,47 | 0,8 | 80% |
| 6 | Агент 5 | 0,5 | 0,7 | 0,3 | 0,4 | 0,74 | 81% |
| 7 | Средняя эффективность пяти агентов | ||||||
| 8 | Средний агент | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | |
Для выполнения задания нужно составить и заполнить таблицу вида:
сделать прогноз продаж на новый квартал и выполнить другие пункты задания.
Для выполнения задания нужно составить таблицу вида:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тираж,тыс. | 100 | 120 | 121,7 | 124,2 | 128 | 130,1 | 133,45 | 136 | 141 | 142,1 | 143,8 | 145 |
| Доход,тыс. руб. | 128 | 135 | 138 | 142 | 147 | 154 | 159 | 161 | 163 | 168 | 170,5 | 172 |
и заполнить ячейки за 12 месяцев условными данными. По этим данным нужно сделать линейный и экспоненциальный прогноз и др. (см. Задание).
Для выполнения задания нужно составить таблицу вида:
| Мес. | Фирма | Конкурент 1 | Конкурент 2 | Конкурент 3 | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | У-объём | х1-цена | х2-объём | х3-цена | х4-объём | х5-цена | х6-объём | х7-цена |
| 2 | 10000 | 1875 | 12000 | 1720 | 12500 | 1740 | 11970 | 1700 |
| 3 | 11000 | 1850 | 12340 | 1705 | 12620 | 1735 | 12100 | 1690 |
| 4 | 11570 | 1810 | 12750 | 1675 | 12740 | 1710 | 12350 | 1645 |
| 5 | 11850 | 1750 | 12910 | 1630 | 12960 | 1695 | 12500 | 1615 |
| 6 | 12100 | 1685 | 13100 | 1615 | 13000 | 1674 | 12630 | 1580 |
| 7 | 12340 | 1630 | 13570 | 1600 | 13210 | 1625 | 12920 | 1545 |
| 8 | 12750 | 1615 | 13820 | 1575 | 13320 | 1610 | 13150 | 1520 |
| 9 | 12910 | 1600 | 13980 | 1515 | 13460 | 1560 | 13300 | 1500 |
| 10 | 13100 | 1575 | 14000 | 1500 | 13600 | 1525 | 13610 | 1490 |
| 11 | 13230 | 1530 | 14070 | 1495 | 13780 | 1500 | 13850 | 1485 |
| 12 | 13470 | 1510 | 14120 | 1488 | 13900 | 1460 | 14000 | 1475 |
| 13 | ||||||||
Для выполнения задания нужно составить таблицу вида:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Доллар | 24,5 | 24,9 | 25,7 | 26,9 | 28,0 | 28,8 | 29,3 | 29,7 | 30,5 | 30,9 | 31,8 | |
| Марка | 72,1 | 76,3 | 79,6 | 85,3 | 89,7 | 90,9 | 93,2 | 96,4 | 100,2 | 101,6 | 104,9 |
и сделать линейный прогноз на следующие 6 месяцев и др. (см. Задание).
Для выполнения задания нужно составить и заполнить таблицу вида:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | месяц | х1 | х2 | х3 | y=у2/у1*100% |
| 2 | 1 | 15 | 10 | 24 | 78% |
| 3 | 2 | 16 | 11 | 23 | 80% |
| 4 | 3 | 18 | 12 | 22 | 81% |
| 5 | 4 | 19 | 12 | 22 | 84% |
| 6 | 5 | 21 | 13 | 21 | 85% |
| 7 | 6 | 22 | 14 | 20 | 89% |
| 8 | 7 |
и выполнить применительно к таблице пункты Задания.
Для выполнения задания нужно составить и заполнить таблицу вида
| Годы | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Расход 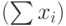 | Доход | Кредит(Y) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 2 | 1,3 | 1 | 0,3 | 5 | 4 | 18,6 | 21,4 | 3,1 |
| 2 | 5,2 | 2,2 | 1,2 | 1,2 | 0,4 | 4,8 | 4,5 | 19,5 | 22 | 2,5 |
| 3 | 5,5 | 2,5 | 1,1 | 1,4 | 0,6 | 4,6 | 4,9 | 20,6 | 23,4 | 2,8 |
| 4 | 5,8 | 2,7 | 0,9 | 1,6 | 1 | 4,2 | 5,6 | 21,8 | 25,8 | 4 |
| 5 | 7 | 3 | 0,8 | 2 | 1,2 | 4 | 6,5 | 24,7 | 26,2 | 1,5 |
| 6 | 7,5 | 3,3 | 0,7 | 2,2 | 1,5 | 3,8 | 7 | 26,5 | 27,5 |
В ячейках столбца 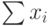
| Квартиры | X1 | X2 | X3 | X4 | X5 | Стоимость ( y ) |
|---|---|---|---|---|---|---|
| 1 | 41 | 33 | 7 | 1 | 2 | 42000 |
| 2 | 40 | 30 | 7,7 | 2 | 3 | 40000 |
| 3 | 45 | 37 | 8 | 0 | 5 | 47000 |
| 4 | 46,3 | 34 | 9 | 1 | 6 | 49500 |
| 5 | 50 | 36 | 9 | 1 | 4 | 51000 |
| 6 | 53 | 40 | 9,5 | 1 | 7 | 55000 |
| 7 | 56 | 41 | 10 | 0 | 9 | 62000 |
| 8 | 60 | 47 | 12 | 2 | 10 | 62300 |
| 9 | 65 | 49 | 14 | 2 | 12 | 69000 |
| 10 | 70 | 58 | 14,5 | 2 | 14 | 72000 |
| 11 | 28 | 16 | 6 | 0 | 1 |
| Годы | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Родились | 100 | 110 | 130 | 155 | 170 | 174 | 180 | 185 | 190 | 200 | |
| Умерли | 108 | 115 | 135 | 160 | 178 | 180 | 186 | 190 | 197 | 205 |
Проанализируйте, связано ли увеличение спроса на матричные принтеры с уменьшением спроса на струйные и лазерные.
| Матричные принтеры | Струйные принтеры | Лазерные принтеры | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Спрос у1 | Цена х1 | Рас.мат. z1 | Спрос у2 | Цена х2 | Рас.мат. z/2 | Спрос у3 | Цена х3 | Рас.мат. z3 | |
| 1 | 56 | 4172 | 174 | 26 | 2384 | 558 | 13 | 12517 | 1558 |
| 2 | 58 | 4250 | 179 | 24 | 2398 | 570 | 11 | 12984 | 1612 |
| 3 | 60 | 4289 | 182 | 23 | 2401 | 598 | 9 | 13259 | 1789 |
| 4 | 65 | 4297 | 194 | 20 | 2456 | 649 | 8 | 13687 | 1865 |
| 5 | 69 | 4305 | 205 | 19 | 2512 | 722 | 7 | 14013 | 1998 |
| 6 | 75 | 4318 | 213 | 18 | 2543 | 768 | 6 | 14587 | 2200 |
| 7 | 4456 | 220 | 17 | 2601 | 779 | 5 | 14789 | 2245 | |
Необходимо сделать прогноз на седьмой месяц по уравнению у1=f(x1,z1), получить уравнение y=(у2,x2, z2, у3, x3, z2 ) и проанализировать его. Если слагаемые у2 и у3 входят в регрессионное уравнение со знаком «-«, то уменьшение спросов у2 и у3 ведёт к увеличению спроса у1.
| Годы | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Динамика населения (тыс. чел) | 21,5 | 26,1 | 31,5 | 34,9 | 45,1 | 50,8 | 56 | 59,4 | 63,9 | 67,1 | |
| Динамика продаж (тыс. шт.) | 2,5 | 2,9 | 3,4 | 3,9 | 4,1 | 4,8 | 5 | 5,6 | 5,9 | 6,2 |
Пользуясь данными таблицы
| Издания | х1 | х2 | х3 | х4 | х5 | х6 | Отклики, у |
|---|---|---|---|---|---|---|---|
| 1 | 10000 | 13 | 700 | 15000 | 4 | 1 | 108 |
| 2 | 12500 | 12 | 850 | 22000 | 8 | 1 | 115 |
| 3 | 15890 | 11,8 | 960 | 28000 | 10 | 0 | 120 |
| 4 | 17850 | 11 | 1200 | 32000 | 26 | 1 | 128 |
| 5 | 15000 | 10 | 1000 | 25000 | 4 | 0 |
необходимо сделать прогноз при заданных характеристиках.
| Месяцы | Издание 1 | Издание 2 | ||
|---|---|---|---|---|
| Звонки | Сделки | Звонки | Сделки | |
| 1 | 98 | 66 | 112 | 79 |
| 2 | 105 | 72 | 143 | 85 |
| 3 | 105 | 75 | 150 | 90 |
| 4 | 110 | 80 | 130 | 100 |
| 5 | 125 | 90 | 120 | 75 |
| 6 | 140 | 100 | 115 | 80 |
| 7 | 136 | 95 | 128 | 82 |
| 8 | 137 | 87 | 132 | 78 |
| 9 | 145 | 102 | 138 | 88 |
| 10 | 123 | 75 | 143 | 92 |
| 11 | 130 | 79 | 150 | 97 |
| 12 | 139 | 88 | 155 | 97 |
| 13 | ||||
Эффективность определяется как сделки/звонки. Сделать линейный и экспоненциальный прогнозы по обоим изданиям.
Пользуясь данными таблицы
сделать прогноз и выполнить другие пункты задания.
| Месяц | Радиостанция 1 | Радиостанция 2 | ||
|---|---|---|---|---|
| Аудитория | Цена 1 мин. | Аудитория | Цена 1 мин. | |
| 1 | 250000 | 8000 | 300000 | 7560 |
| 2 | 540000 | 6500 | 450000 | 6340 |
| 3 | 580000 | 6460 | 490000 | 6250 |
| 4 | 650000 | 6300 | 550000 | 6000 |
| 5 | 730000 | 6060 | 610000 | 5730 |
| 6 | 750000 | 6000 | 690000 | 5300 |
| 7 | 800000 | 5400 | 750000 | 5100 |
| 8 | 840000 | 5320 | 780000 | 5000 |
| 9 | 890000 | 5130 | 870000 | 4700 |
| 10 | 950000 | 5000 | 900000 | 4650 |
| 11 | 1000000 | 4800 | 940000 | 4600 |
| 12 | 1108000 | 4700 | 1025000 | 4540 |
| 13 | ||||
| Контакт | ||||
В строке «Контакт» в ячейках С8 и D8 должны быть записаны формулы = С7/В7 и =Е7/D7 соответственно, вычисляющие стоимость 1 мин. Эфира для одного слушателя в прогнозируемом месяце. Прогноз нужно выполнить для линейного и экспоненциального приближений и выбрать более достоверный, а также сделать другие пункты Задания.
Определить возможное изменение количества вкладчиков данного банка в следующем месяце, если известны значения сфер рейтинга и количество вкладчиков в каждом из рассматриваемых 6 месяцев.
📺 Видео
Критерий Фишера для проверки адекватности построенной регрессииСкачать

Парная регрессия: линейная зависимостьСкачать

Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Устный доклад Статистическая оценка надежности параметров парной регрессии и корреляцииСкачать

Множественная регрессия в ExcelСкачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

04 04 Надежность и стандартная ошибкаСкачать

Множественная регрессия в MS Excel. Быстрое решение. И подробное решение. Калькулятор!Скачать
Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Коэффициент линейной регрессии, 2 способаСкачать

РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать
Множественная регрессияСкачать

Лекция 2.1: Линейная регрессия.Скачать

Эконометрика Линейная регрессия и корреляцияСкачать