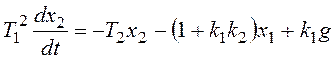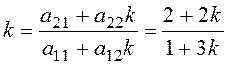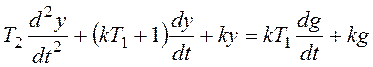§16. ФАЗОВАЯ ПЛОСКОСТЬ
Фазовая кривая системы уравнений 
— это проекция интегральной кривой на фазовую плоскость. Фазовая траектория является решением уравнения 
которое можно решить методом изоклин. Для построения фазовой траектории уравнения второго порядка 
необходимо свести последнее к системе 
Начертить фазовую кривую уравнения 
Решение. Сведём уравнение к системе 
Уравнение для фазовой кривой имеет вид 
Решая его, получим ydy = 4 xdx Þ y 2 /2 – 2 x 2 = C . Фазовые траектории 
— это семейство гипербол, изображённых на рис. 3.
[an error occurred while processing this directive]
Начертить фазовую траекторию уравнения 
Решение. Сведём уравнение к системе 
Фазовые траектории – это решение уравнения 
Решая последнее уравнение, получим
ydy = — 2x 3 dx Þ y 2 /2 + x 4 /4 = C.
Семейство кривых y 2 /2С + x 4 /4С = 1 похоже на семейство эллипсов. Направление движения траектории определено по исходной системе.
[an error occurred while processing this directive]
Начертить фазовые траектории уравнения 
Решение. Сведём к системе 
Уравнение фазовых кривых 
Его особые точки у = 0, х = p k,
k = 0, ± 1, … Фазовые кривые изображены на рис. 5.
Как математик Михаил Васильевич Остроградский пользовался огромной славой. О его учебнике геометрии для военных школ Н. Г. Чернышевский писал, что, не читая книгу, можно сказать о ее больших достоинствах, так как автором этой книги является знаменитый Остроградский Еще в детстве Миша Остроградский увлекался разного рода измерениями. Он измерял комнаты, мебель и даже свои игрушки
Видео:Устойчивость 1 ОпределениеСкачать
Анализ особых точек и построение фазовых портретов линейных систем
Страницы работы
Содержание работы
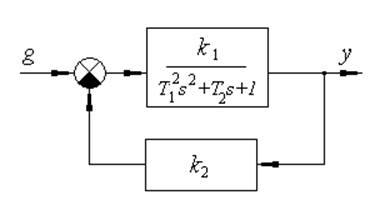
Практическое занятие 7.Анализ особых точек и построение фазовых портретов линейных систем.
Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.
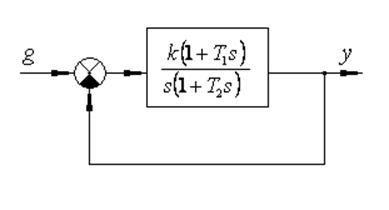
Перейдем к модели в форме системы дифференциальных уравнений:
,
.
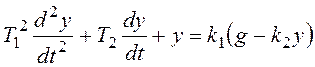
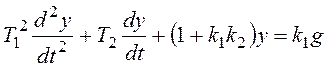
Отсутствие производных входного сигнала в правой части уравнения позволяет ввести фазовые переменные наиболее удобным для построения фазового портрета образом: x1=y,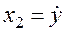 
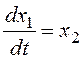
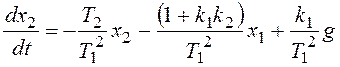
. В результате получим:
,
.
Подставим в уравнения числовые данные:
,
.
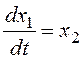
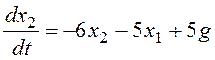
Рассчитаем координаты особой точки (у линейной системы особая точка возможна только одна):
,
, 
.
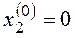
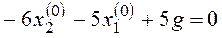
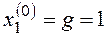
Составим матрицу А и найдем ее собственные числа:
,
,
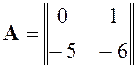
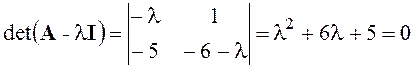
Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (1; 0) – устойчивый узел.
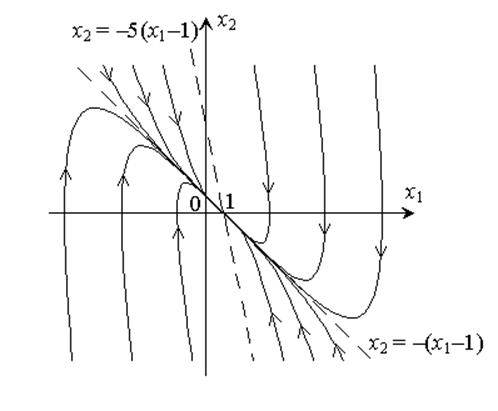
Для рассматриваемого базиса собственные числа матрицы А определяют наклон особых линий на фазовой плоскости. Особые линии – прямые x2 = –(x1–1) (касательная к фазовым траекториям в особой точке) и x2 = –5(x1–1).
Примерный фазовый портрет показан на рисунке.
Модель задана в форме системы уравнений:
,
.
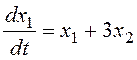
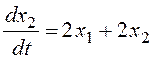
Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.
Рассчитаем координаты особой точки:
,
.
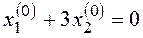
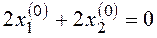
Такая система имеет «тривиальное» решение:
, .
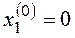
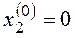
Найдем собственные числа матрицы А:
,
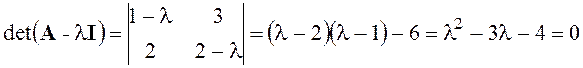
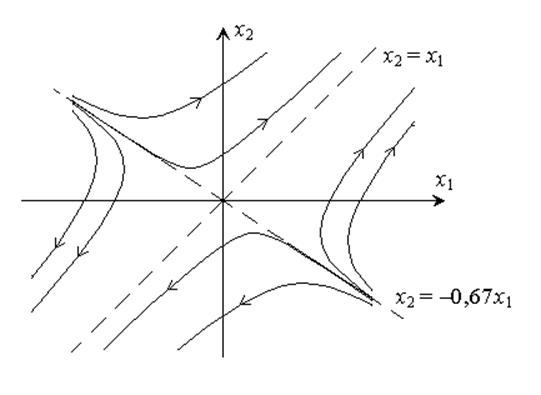
Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (0; 0) – седло.
Фазовые траектории – гиперболы. Особые линии – асимптоты гипербол. Их наклоны найдем из уравнения
,
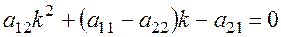
Для определения направления движения по фазовым траекториям найдем значения составляющих вектора скорости движения, например, в точке (0; 1):
,
.
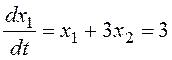
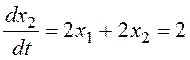
Вектор скорости в рассмотренной точке направлен вправо и вверх.
Примерный фазовый портрет показан на рисунке.
Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.
Запишем общее дифференциальное уравнение системы
и перейдем к модели в форме системы дифференциальных уравнений:
,
,
,
,
,
, или в числах:
,
.
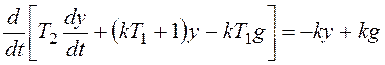
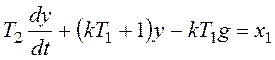
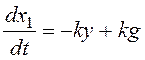
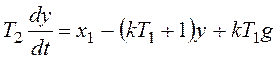
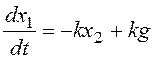
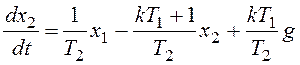
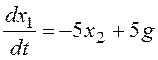
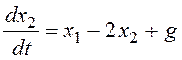
Рассчитаем координаты особой точки:
,
;
,
.
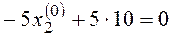
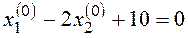
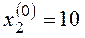
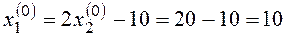
Найдем собственные числа матрицы А:
,
.
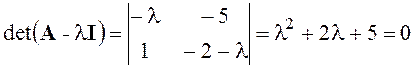
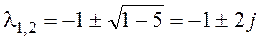
Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (10; 10) – устойчивый фокус.
Фазовые траектории – сходящиеся в особую точку спирали. Направление движения по фазовым траекториям определим, рассчитав составляющие вектора скорости движения изображающей точки, например, в начале координат:
,
.
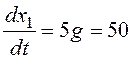
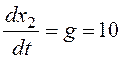
Таким образом, если ось x1 выбирается в качестве горизонтальной, направление движения по фазовым траекториям – против часовой стрелки.
Видео:4. Исследование фазовых траекторий.Скачать
Метод фазовой плоскости
Основные понятия. Состояние любой динамической системы, описываемой дифференциальным уравнением я-го порядка, может быть определено в любой момент времени значениями п переменных, например регулируемой координаты х и п — 1 ее производных в «-мерном пространстве, называемом фазовым пространством системы. Это состояние характеризуется координатами изображающей точки, откладываемыми по осям фазового пространства. В установившемся режиме системы изображающая точка занимает фиксированное положение и называется особой точкой. В переходном режиме координаты х и п — 1 сс производных будут изменяться, обусловливая движение изображающей точки по фазовой траектории. Характер этого движения и положение фазовых траекторий в фазовом пространстве определяются динамическими свойствами системы и начальными условиями. Полная совокупность фазовых траекторий, соответствующая всем возможным начальным условиям, называется фазовым портретом системы. Двухмерное фазовое пространство представляет собой фазовую плоскость.
Метод фазовой плоскости позволяет исследовать динамические свойства систем, описываемых нелинейными уравнениями 1-го и 2-го порядков:
Системы, содержащие элементы, характеристики которых обладают зонами неоднозначности, не могут быть отображены на обычной фазовой плоскости и требуют для своего отображения многолистных фазовых поверхностей. Движение системы в этом случае описывается уравнениями, подобными (11.1), но каждая из систем уравнений определена нс на всей фазовой плоскости, а только на некоторых площадях, которые перекрывают друг друга.
При изображении фазового портрета на плоскости уравнение 2-го порядка заменяется системой двух уравнений:
Исключив из уравнения (11.2) время, получим dy/djt = F(:с, у)/у.
Решение этого нелинейного дифференциального уравнения дает зависимость
которая определяет фазовую траекторию.
Фазовые портреты линейных систем. Рассмотрим фазовые траектории, определяемые уравнением 2-го порядка, для линейной системы. Пусть дано дифференциальное уравнение
Исключив из уравнений (11.4) время делением одного на другое, получим 
Согласно уравнениям (11.2) оно может быть представлено в следующем виде:
Использовав подстановку 
и проинтегрировав это уравнение, получим
Результат интегрирования левой части уравнения (11.5) зависит от корней характеристического уравнения (и 2 + + д0) = О,
которые определяются из выражения
При отсутствии демпфирования (д, = 0) получим чисто мнимые корни 5j 2 = ±/о), (0= у/а 2 — 4до /2. Решение уравнения (11.3),
имеющее вид х = jocose)./, показывает, что в системе устанавливаются незатухающие гармонические колебания (рис. 11.2, а).
Уравнение (11.5) в случае мнимых корней принимает вид
Обозначив С = 1по)С| и учитывая, что и = у/х, получим уравнение семейства фазовых траекторий, имеющих вид эллипсов:
с полуосями о)С| и С| (см. рис. 11.2, а). Изображающая точка, движущаяся по часовой стрелке, при незатухающих синусоидальных колебаниях описывает замкнутый контур. Центром эллипса является особая точка, в которую стягиваются эллипсы при изменении С,.
При положительном демпфировании (ду > 0) и условии а 2 , а для участка 2 — bsgn(x) = -b. Уравнение линий переключения имеет вид х- 0, так как эта линия, согласно характеристике реле, совпадает с осью ординат.
Для построения фазовой траектории, например на участке 2, выбирается произвольная точка с координатами лг0 и Уо- Затем по уравнению (11.14) для участка 2 при />sign(x) = -b строится фазовая траектория вплоть до линии переключения. Для построения фазовой траектории на участке 1 в уравнение (11.14) подставляется ^ign(x) = />, за начальные условия принимаются конечные значения х и у, полученные на линии переключения при расчете фазовых траекторий на участке 2, и т.д.
На рис. 11.4, б приведен примерный вид фазового портрета, рассчитанного этим методом. Он показывает, что система устойчива в целом. Теоретически в подобной двухпозиционной релейной системе в начале координат должны существовать устойчивые автоколебания с бесконечно малой амплитудой и бесконечно большой частотой.
При применении трехпозиционного реле фазовый портрет имеет две линии переключения, параллельные оси ординат и отстоящие от нее вправо и влево на расстоянии а. Уравнение линий переключения имеет вид х = ±а.
📸 Видео
Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать
ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать
Лекция №5 Фазовые траектории автономных систем (разбор примеров)Скачать
ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать
Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать
Волков В. Т. - Дифференциальные уравнения - Фазовая плоскость. Фазовые траектории и их видыСкачать
Дифференциальные уравнения 20. Исследование поведения фазовых траекторийСкачать
Гордон. Убийство Навального: где тело и где его похоронят. Отход из Авдеевки. США бросили Украину?Скачать
Филиппов №881(г) — Исследование решения на устойчивостьСкачать
Нефёдов Н. Н. - Дифференциальные уравнения - Фазовая плоскость. Асимптотические методыСкачать
Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать
Особые точки 4 ЗадачаСкачать
Решение системы дифференциальных уравнений методом ЭйлераСкачать
4 Системы 2х2Скачать
Дифференциальные уравнения 3. Автономные системыСкачать
