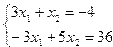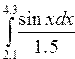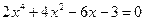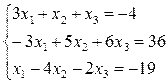- Реферат.Справочник
- Контрольные работы по информатике
- Построить график заданной y=F(x) (Таблица 3). На заданном диапазоне изменения аргумента найти все корни уравнения F(x)=0 и построить график функции
Условие
Построить график заданной y=F(x) (Таблица 3). На заданном диапазоне изменения аргумента найти все корни уравнения F(x)=0 и построить график функции. Таблица 3. Функция Диапазон изменения Шаг y=0,25+sinx-cosx2 2,5;3,5 0,05
Решение
Решение состоит из двух этапов:
Отделение корней;
Уточнение корней.
1-й этап. Отделение корней.
Построим таблицу значений и график функций y=F(x) на интервале 2,5;3,5 и определим промежутки, на которых функция меняет знак (Рис . 4). На этих промежутках и будут находиться корни уравнения F(x)=0.
Рис. 4. Отделение корней уравнения
Таким образом, для исходного уравнения таких промежутков будет два: промежуток 2,65;2,7 и промежуток 3,3;3,35.
2-й этап
Зарегистрируйся, чтобы продолжить изучение работы
. 4). На этих промежутках и будут находиться корни уравнения F(x)=0.
Рис. 4. Отделение корней уравнения
Таким образом, для исходного уравнения таких промежутков будет два: промежуток 2,65;2,7 и промежуток 3,3;3,35.
2-й этап
Оплатите контрольную работу или закажите уникальную работу на похожую тему
Видео:Решение систем линейных уравнений в Scilab.aviСкачать

Тема урока: «Решение трансцендентных уравнений»
Цель урока: нахождение корней уравнений математическим способом, проверка решения с помощью компьютера.
Познавательная – применение компьютерных технологий при решении уравнений, использование их при подготовке к ЕГЭ.
Закрепление навыков решения трансцендентных уравнений, проверка знаний учащихся по данной теме.
Развивающая – умение осуществлять взаимосотрудничество, применять знания смежных наук — математики и информатики. Развитие логического мышления учащихся.
Воспитательная – развитие коммуникативных навыков, интереса к учебном предметам. Воспитание ответственного отношения к коллективному труду.
Тип урока: повторительно-обобщающий, межпредметный интегрированный.
Метод: работа группами.
Форма работы: дидактическая игра.
Оборудование : Плакаты, карточки-задания, жетоны, ЭВМ.
1. Организационный момент. Рапорт дежурного командира об отсутствующих
2. Сообщение темы и цели урока.
3. Разминка: а) устный опрос по определениям (математика)
б) решение уравнений по готовым карточкам.
в) устный опрос по определениям (информатика)
4. Решение уравнений в группах за учебным столом и ЭВМ.
5. Оформление протоколов по группам.
6. Подведение итогов (ход урока на доске, оформление газеты-репортажа силами жюри). Награждение победителей соревнования.
7. Домашнее задание. Решить уравнения с использованием ЭВМ (задания ЕГЭ – см приложение “Домашнее задание”)
Класс разбит на три группы, включающие разноуровневый контингент учащихся
- ПОВТОРЕНИЕ — разминка
а) устный опрос по определениям (каждой из трех команд задается по три вопроса):
1. Определение (уравнения).
Любое выражение вида f (x) = g (x), где f (x) и g (x) – некоторые функции, называется уравнением с одной переменной x (или с одним неизвестным х). Функция f (x) называется левой частью, а g (x) – правой частью уравнения.
2. Определение (корня уравнения).
Число а называется корнем (или решением) данного уравнения с переменной х, если при подстановке числа а вместо х в обе части этого уравнения получаем верное числовое равенство, т.е., если при х = а обе части уравнения определены и их значения совпадают.
3. Что значит решить данное уравнение?
Решить данное уравнение — значит найти множество всех корней (решений) этого уравнения в области R или доказать, что данное уравнение не имеет корней.
4. Определение (числовой функции).
Числовой функцией с областью определения Д называется соответствии, при котором каждому числу х из множества Д сопоставляется по некоторому правилу число у, зависящее от х.
5. Определение (области определения функции), Д(f).
Областью определения функции называется множество значений переменной х при которых функция определена, или существует, или имеет смысл.
6. Определение (области значения функции), Е(f).
Областью значения функции называется множество значений переменной у, которые принимает функция.
7. Определение (графика функции).
Графиком функции f(х) называется множество всех точек (х, у) координатной плоскости, где у = f(х), а х “пробегает” всю область определения функции f(х).
8. Определение (области определения уравнения).
Областью определения уравнения называется общая часть области определения каждой из функций f(x) и g(x) (говорят: пересечение областей определения функций).
9. Определение (трансцендентного уравнения).
Уравнение вида: f(x) = g(x) или v(x) =0, в которых функции f(x), g(x), v(x) показательная, логарифмическая или тригонометрическая принято называть трансцендентными уравнениями.
(Оценка работы — выдача жетона –кружка зелёного цвета –1 балл).
б) решение уравнений по готовым карточкам (каждой из трех команд предлагается решить по три уравнения. Уравнения для каждой команды написаны на небольших плакатах или можно написать на доске. Данные уравнения прилагаются (см приложение “Математическая разминка”).
Свои решения уравнений каждая команда оформляет на местах, а ответы записываются на доске против каждого уравнения. Учитель или консультант проверяет решение и ответ каждого уравнения или показывает учащимся заранее заготовленное решение каждого уравнения.
(Оценка — группе, закончившей работу первой даётся пять баллов, вторым – 4, третьим – 3 балла: жетоны красного цвета-5, синего – 4, жёлтого — 3).
1. Чем определяется положение точки на координатной плоскости ?
2. Таким образом, для построения графика необходимо задать область определения аргумента Х и область значений Y. Как задать область определения аргументов?
(в программе электронных таблиц “Excel” с помощью автозаполнения задать предложенный в задании отрезок изменения значений абсцисс и шаг изменения)
3.Для задания области значений функции необходимо ввести формулу функции. Как записывается формула в ячейке Э.Т.?
(например Y=2X как =2*A3, где A3-адрес ячейки со значением абсциссы)
4. Как быстро ввести эту формулу в таблицу задания значений ординат?
5. Что такое “легенда”? Её назначение?
(область внутри диаграммы с информацией о построенных графиках)
6. Где помещается запись формулы для простоты её расположения в легенде?
(в таблице задания значений Y в первой ячейке в виде текста Y=2X)
7. Где задаётся эта запись?
8. Для активизации “Мастера диаграмм” необходимо задать область адресов ячеек с вычисленными значениями функции, как это сделать?
(в созданной таблице выделить область ячеек со значениями, вызвать “Мастера диаграмм”, в вкладке “Диапазон данных” они автоматически укажутся)
9. Как для “Мастера диаграмм” задать область изменения аргумента для отображения их значений в диаграмме?
(свернуть диалоговое окно, выделить диапазон ячеек со значениями аргументов, при этом курсор должен находиться во вкладке “Ряд” в рамке “Подписи по оси Х”)
(Оценка работы — выдача жетона – кружка зелёного цвета – 1 балл).
б) повторение терминалогии Э.Т. – игра домино по группам
Необходимо сложить ряд из определений (см. приложение “Домино ЭТ”)(Оценка: группе, закончившей работу первой даётся пять баллов, вторым – 4, третьим – 3 балла)
а) Решить уравнение алгебраически, решение оформить на листе (каждое уравнение на отдельном).
б) Используя электронные таблицы (Excel), построить на экране два графика, условие одного слева от знака равенства, другого справа. Точка их пересечения (значение абсциссы) даст корень.
в) Заполнить протокол — отчёт, где указать условие, отрезок значений аргумента (х), шаг его изменения, полученные корни (в процессе алгебраического решения и на ЭВМ ), показав график учителю информатики, сдав листок с решением учителю математики.
Ваши решения будут оценены.
Решение трансцендентных уравнений (протокол)
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Вычисление интегралов, решение уравнений и систем
Краткие теоретические сведения
В Scilab вычисление определенного интеграла методом трапеций реализовано функцией
где x –вектор значений аргумента подынтегральной функции на отрезке интегрирования, y –вектор значений, полученных при вычислении подынтегральной функции для элементов вектора x.
Например, для вычисления 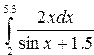
| Фрагмент программы x=2:0.01:5.3 y =2*x./(sin(x)+1.5) integral = inttrap(x,y)disp(integral) | Результат 30.436962 |
Для вычисления определенного интеграла с использованием алгоритма квадратурных формул предназначена функция
Integrate(fun, x, a, b, ,er1 ,er2),
где fun– подынтегральная функция в символьном виде, x – переменная интегрирования в символьном виде, a, b –пределы интегрирования, er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры).
Например, для вычисления 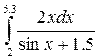
| Фрагмент программы z=integrate(‘2*x./(sin(x)+1.5)’, ‘x’, 2, 5.3)disp(z) | Результат 30.437056 |
Универсальная команда интегрирования:
[integral,err]=intg(a, b, name ,er1,er2),
где a, b –пределы интегрирования, name – имя подынтегральной функции (может быть задана с помощью внешней функции), er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры). Функция intgвозвращает значение интеграла (integral) и погрешность вычислений (err).
Внешнюю функцию можно задать командой
deff(‘переменная=имя функции(параметр)’, ‘символьное представление функции’) Например, deff(‘y=F(x)’, ‘y=2*x./(sin(x)+1.5)’).или
function переменная = имя функции(параметр-аргумент функции)
операторы, вычисляющие значение функции
endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction
Ниже приводится пример вычисления интеграла 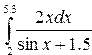
| Фрагмент программы function y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z) | Результат 30.437056 |
Для решения нелинейных уравнений в Scilab используется функция
где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.
Например, для решения уравнения 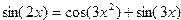
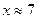
| Фрагмент программы deff(‘y=F(x)’, ‘y=sin(2*x)-cos(3*x.^2)-sin(3*x)’)root=fsolve(7,F)disp(root) | Результат 6.9755674 |
Для решения полиномиальных уравнений вида 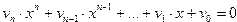
где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
Результатом работы этой функции будет вектор корней полинома размерностью n.
Пример решения полиномиального уравнения 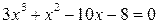
| Фрагмент программы v=[3 1 -10 -8]R=roots(v)disp(R) | Результат 2. -1.3333333 — 1. |
Для уравнения 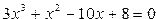
| Фрагмент программы v=[3 1 -10 8]R=roots(v)disp(R) | Результат — 2.2935835 0.9801251 + 0.4494650i 0.9801251 — 0.4494650i |
Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения 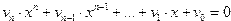
где a –вектор коэффициентов полинома записанных в обратном порядке, x — символьная переменная, f1– символьная переменная, принимающая значения ‘c’ или ‘r’ (roots или coeff).
Например, чтобы создать полином 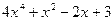
| Фрагмент программы p=poly([3 -2 1 0 4],’x’,’c’)disp(p) | Результат 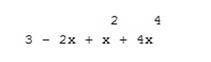 |
Для решения уравнения 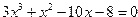
| Фрагмент программы p=poly([-8 -10 1 3],’x’,’c’)R=roots(p)disp(R) | Результат 2. — 1.3333333 — 1. |
Для решения систем линейных уравнений в Scilab есть следующие способы:
— применение операции левого матричного деления;
— использование обратной матрицы.
Если задана система линейных алгебраических уравнений вида:
где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:
То же самое решение может быть получено с помощью обратной матрицы, например:
Например, решить систему уравнений
| Фрагмент программы A=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)илиX1=AB , disp(X1) | Результат — 3.1111111 5.3333333 |
Для решения систем нелинейных уравнений можно использовать функцию
где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему
Например, решение системы 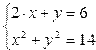
| Фрагмент программы function [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R) | Результат 1.2338096 3.5323808 |
Задание 1. Вычисление определенного интеграла
Постановка задачи. Вычислить числовое значение интеграла от этой функции в заданных пределах интегрирования методом трапеций, методом квадратурных формул и с помощью функции intg.
Шаг 1. Создадим вектор X, значения которого будут изменяться от 2,1 до 4,3 с шагом 0.01.
Шаг 2. Создадим вектор Y, каждое значение которого вычисляется по формуле 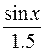
Шаг 3. Применим команду inttrap(X, Y).
Шаг 4. Используем функцию integrate,задав подынтегральную функцию в символьном виде.
Шаг 5. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 6. Выведем результаты, используя команду disp.
| Программа | Результат выполнения |
| X =2.1:0.01:4.3 Y =sin(X)/1.5 integral_1 = inttrap(X,Y)integral_2=integrate(‘sin(x)/1.5’, ‘x’, 2.1, 4.3)disp(integral_1)disp(integral_2) | — 0.0693640 — 0.0693646 |
| deff(‘y=F(x)’,’y=sin(x)/1.5′); integral_3=intg(2.1,4.3,F)function y=f(x) y=sin(x)/1.5endfunctionintegral_4=intg(2.1,4.3,f)disp(integral_3)disp(integral_4) | — 0.0693646 — 0.0693646 |
Индивидуальные задания приведены в таблице 3.4.
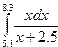 | 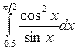 | 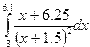 |
 | 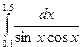 | 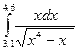 |
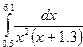 | 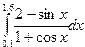 | 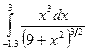 |
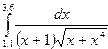 | 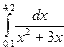 | 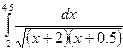 |
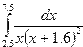 | 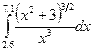 | 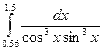 |
Задание 2. Поиск корней уравнения, графическая интерпретация
Постановка задачи. Найти корень уравнения для заданного начального приближения. Выполнить графическую интерпретацию результата.
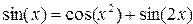 |  |
Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 2. Найдем корень уравнения с помощью функции fsolve,подставив в качестве первого параметра заданное начальное приближение.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| deff(‘y=F(x)’, …’y=sin(x)-cos(x.^2)-sin(2*x)’)root=fsolve(1,F)disp(root)x=0.5:0.01:2.5plot(x,F(x),’-b’,root,F(root),’xr’,x,0,’-k’) | 1.1695683 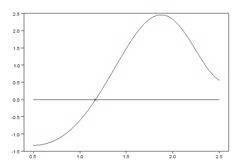 |
Индивидуальные задания приведены в таблице 3.5
| Вариант | Уравнение | Начальноеприближение |
| 1. | 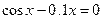 | 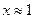 |
| 2. | 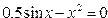 | 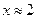 |
| 3. | 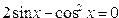 | 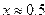 |
| 4. | 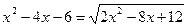 | 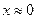 |
| 5. | 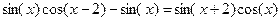 | 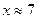 |
| 6. | 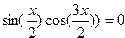 |  |
| 7. | 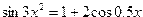 | 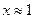 |
| 8. | 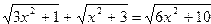 | 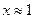 |
| 9. | 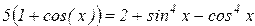 | 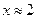 |
| 10. | 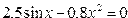 | 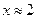 |
| 11. | 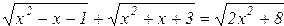 | 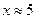 |
| 12. | 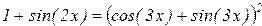 | 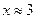 |
| 13. | 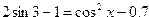 | 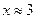 |
| 14. |  | 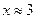 |
| 15. | 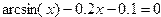 | 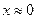 |
Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация
Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.
Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)
Шаг 2. Найдем корни уравнения с помощью функции roots.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,’-b’,root,F_root,’xr’,x,0,’-k’) | — 0.4129576 + 1.7282075i — 0.4129576 — 1.7282075i 1.2164706 — 0.3905555 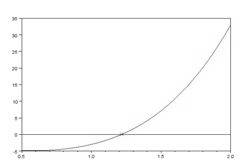 |
Индивидуальные задания приведены в таблице 3.6.
| Вариант | Уравнение |
| 1. | 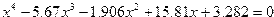 |
| 2. |  |
| 3. | 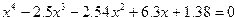 |
| 4. | 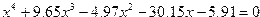 |
| 5. | 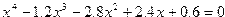 |
| 6. | 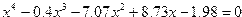 |
| 7. | 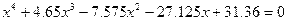 |
| 8. | 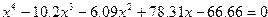 |
| 9. | 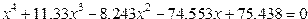 |
| 10. | 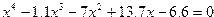 |
| 11. | 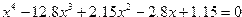 |
| 12. | 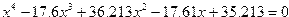 |
| 13. | 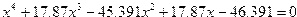 |
| 14. |  |
| 15. | 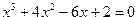 |
Задание 4. Решение системы линейных уравнений
Постановка задачи. Решить систему линейных уравнений.
Шаг 1. Создадим матрицу коэффициентов при неизвестных
Шаг 2. Создадим вектор свободных членов.
Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).
Шаг 4. Выведем результат, используя команду disp.
| Программа | Результат выполнения |
| A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4 ;36;-19]; X=inv(A)*B disp(X) | — 3. 3. 2. |
Индивидуальные задания приведены в таблице 3.7.
| № | Система уравнений | № | Система уравнений |
| 1. | 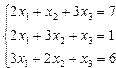 | 2. | 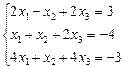 |
| 3. | 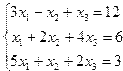 | 4. | 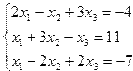 |
| 5. | 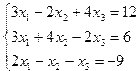 | 6. | 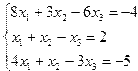 |
| 7. | 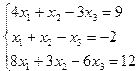 | 8. | 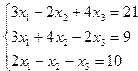 |
| 9. | 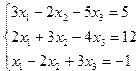 | 10. | 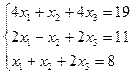 |
| 11. | 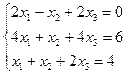 | 12. | 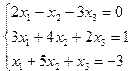 |
| 13. | 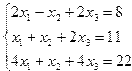 | 14. | 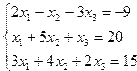 |
| 15. | 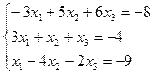 | 16. | 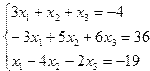 |
Статьи к прочтению:
Метод Крамера за 3 минуты. Решение системы линейных уравнений — bezbotvy
Похожие статьи:
Приближенное вычисление интегралов Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому…
Задание: графически и численно решить систему нелинейных алгебраических уравнений, на примере поиска точек пересечения двух функций. Исходные данные:…
🔍 Видео
Найти корень уравнения на заданном интервале (MathCad)Скачать

#123 Урок 48. Теорема Виета. Подбор корней квадратного уравнения. Алгебра 8 класс. Математика.Скачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
Алгоритмы. Нахождение корней уравнения методом хордСкачать

A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать

🔴 Найдите корень уравнения (1/7)^(x-5)=49 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Как использовать функцию ВПР (VLOOKUP) в ExcelСкачать

Как Решать Задачи на Моногибридное Скрещивание — Биология 10 класс // Подготовка к ЕГЭ по БиологииСкачать

Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 1ч. 10 класс.Скачать

Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Моногибридное скрещивание - правило единообразия и правило расщепленияСкачать

21.04 - дискра, рекуррентные соотношенияСкачать
Установление эмпирической и молек. формул по массовым долям элем., входящих в состав в-ва. 10 класс.Скачать

Алгоритм ДейкстрыСкачать

🔴 Найдите корень уравнения (x-8)^2=(x-2)^2 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать