На вкладке параметры устанавливаем флажки показать уравнение на диаграмме (2 видео)

Построение линий тренда

Дата добавления: 2013-12-23 ; просмотров: 17187 ; Нарушение авторских прав

Построение графиков

Регрессионный анализ

Уравнением регрессии Y от X называют функциональную зависимость у=f(x), а ее график – линией регрессии.

Excel позволяет создавать диаграммы и графики довольно приемлемого качества. Excel имеется специальное средство — Мастер диаграмм, под руководством которого пользователь проходит все четыре этапа процесса построения диаграммы или графика.

Как правило, построение графика начинают с выделения диапазона, содержащего данные, по которым он должен быть построен. Такое начало упрощает дальнейший ход построения графика. Однако диапазон с исходными данными можно делить и на втором этапе диалога с МАСТЕРОМ ДИАГРАММ. В Еxcel 2003 МАСТЕР ДИАГРАММ находится в меню в виде кнопки или диаграмму можно создать путем нажатия на вкладку ВСТАВКА и в открывшемся списке найти пункт ДИАГРАММА. В Excel 2007 также находим вкладку ВСТАВКА (рис. 31).

Рис. 31. МАСТЕР ДИАГРАММ в Excel 2007

Наиболее просто выделить диапазон исходных данных, в котором эти данные находятся в смежных рядах (столбцах или строках), — надо щелкнуть по левой верхней ячейке диапазона и затем протащить указатель мыши до правой нижней ячейки диапазона. При выделении данных, находящихся в несмежных рядах, указатель мыши перетаскивают по выделяемым рядам при нажатой клавише Ctrl. Если один из рядов данных имеет ячейку с названием, остальные выделенные ряды также должны иметь соответствующую ячейку, даже если она пустая.

Для проведения регрессионного анализа лучше всего использовать диаграмму типа Точечная (рис. 30). При ее построении Excel воспринимает первый ряд выделенного диапазона исходных данных как набор значений аргумента функций, графики которых нужно построить (один и тот же набор для всех функций). Следующие ряды воспринимаются как наборы значений самих функций (каждый ряд содержит значения одной из функций, соответствующие заданным значениям аргумента, находящимся в первом ряду выделенного диапазона).

В Excel 2007 названия осей ставятся во вкладке меню МАКЕТ (рис. 32).

Рис. 32. Настойка названий осей графика в Excel 2007

Для получения математической модели необходимо построить на графике линию тренда. В Excel 2003 и 2007 нужно щелкнуть правой кнопкой мыши на точки графика. Тогда в Excel 2003 появится вкладка с перечнем пунктов, из которых выбираем ДОБАВИТЬ ЛИНИЮ ТРЕНДА (рис. 33).

Рис. 33. ДОБАВИТЬ ЛИНИЮ ТРЕНДА

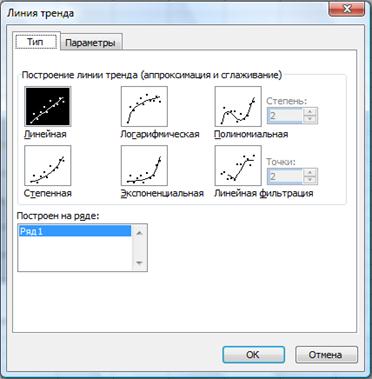
После нажатия на пункт ДОБАВИТЬ ЛИНИЮ ТРЕНДА появится окно ЛИНИЯ ТРЕНДА (рис. 34). Во вкладке ТИП можно выбрать следующие типы линий: линейная, логарифмическая, экспоненциальная, степенная, полиномиальная, линейная фильтрация.

Рис. 34. Окно ЛИНИЯ ТРЕНДА в Excel 2003

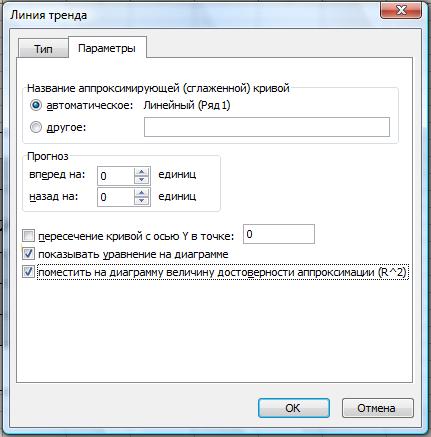
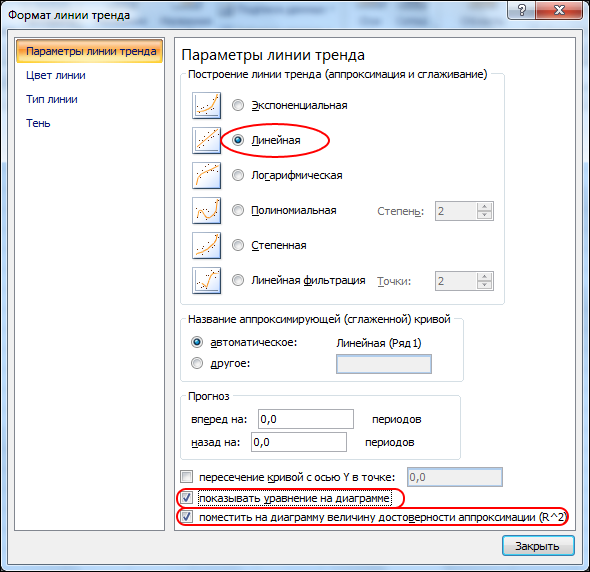
Во вкладке ПАРАМЕТРЫ (рис. 35)устанавливаем флажок напротив пунктов ПОКАЗЫВАТЬ УРАВНЕНИЕ НА ДИАГРАММЕ, тогда на графике появится математическая модель данной зависимости. Также флажок ставим напротив пункта ПОКАЗЫВАТЬ НА ДИАГРАММЕ ВЕЛИЧИНУ ДОСТОВЕРНОСТИ АППРОКСИМАЦИИ (R^2). Чем ближе величина достоверности аппроксимации к 1, тем ближе подходит выбранная кривая к точкам на графике. Далее нажимаем на кнопку ОК. На графике появится линия тренда, соответствующее ей уравнение и величина достоверности аппроксимации.

Рис. 35. Вкладка ПАРАМЕТРЫ

В Excel 2007 после того, как щелкнем правой кнопкой мыши на точки графика, появится список пунктов меню, из которого ВЫБИРАЕМ ДОБАВИТЬ ЛИНИЮ ТРЕНДА (рис. 36).

Рис. 36. ДОБАВИТЬ ЛИНИЮ ТРЕНДА

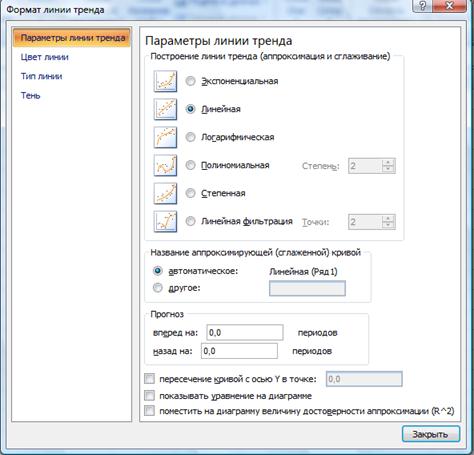
Далее откроется окно ФОРМАТ ЛИНИИ ТРЕНДА с вкладкой ПАРАМЕТРЫ ЛИНИИ ТРЕНДА (рис. 37).

Рис. 37. Вкладка ПАРАМЕТРЫ ЛИНИИ ТРЕНДА

Устанавливаем необходимые флажки и нажимаем кнопку ЗАКРЫТЬ.

На графике появится линия тренда, соответствующее ей уравнение и величина достоверности аппроксимации.

Видео:Как на диаграмме Excel отобразить проекции точек на оси координатСкачать

На вкладке параметры устанавливаем флажки показать уравнение на диаграмме

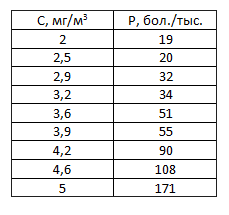
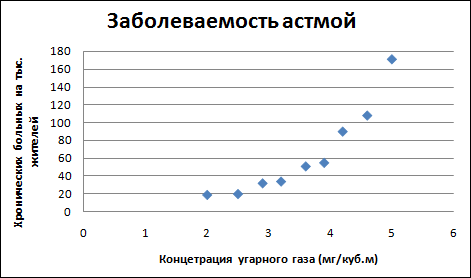
1. Ввести табличные данные зависимости заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере (см. рисунок).
2. Представить зависимость в виде точечной диаграммы (см. рисунок).

Требуется получить три варианта регрессионных моделей (три графических тренда) зависимости заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере.

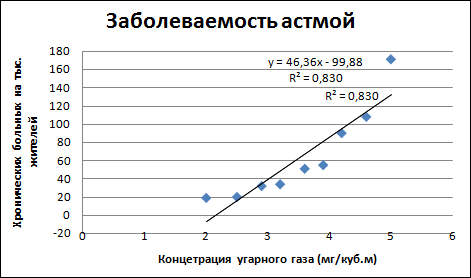
1. Для получения линейного тренда выполнить следующий алгоритм:
=> щелкнуть на поле диаграммы «Заболеваемость астмой», построенной в предыдущем задании;
=> выполнить команду Диаграмма -> Добавить линию тренда ;
=> в открывшемся окне на вкладке Тип выбрать Линейный тренд ;
=> перейти на вкладку Параметры ; установить галочки на флажках:
п оказывать уравнения на диаграмме и поместить на диаграмму величину достоверности аппроксимации R

2 ;
=> щелкнуть на кнопке ОК .

Полученная диаграмма представлена на рисунке:

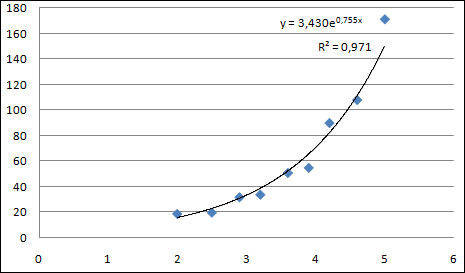
2. Получить экспоненциальный тренд. Алгоритм аналогичен предыдущему. На закладке Тип выбрать Экспоненциальный тренд . Результат представлен на рисунке:

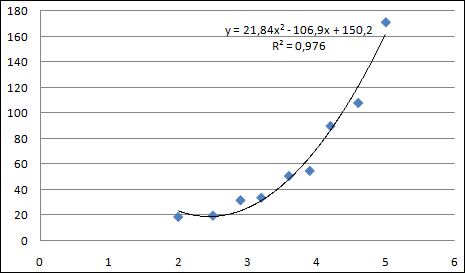
3. Получить квадратичный тренд. Алгоритм аналогичен предыдущему. На закладке Тип выбрать Полиномиальный тренд с указанием степени 2. Результат представлен на рисунке:

После того как вы построили точечную диаграмму зависимости заболеваемости астмой, нужно построить линию тренда .

1. Для этого необходимо выделить диаграмму.
2. В результате выделения в панели инструментов появятся новые разделы. Из этих разделов нам нужно будет перейти в вкладку «Макет» .

3. Из макета нужно перейти в раздел «Анализ» , где мы и найдём операцию построения линии тренда.

Сразу строить линию тренда не советуется, так как нам нужно указать определённые настройки отображения.

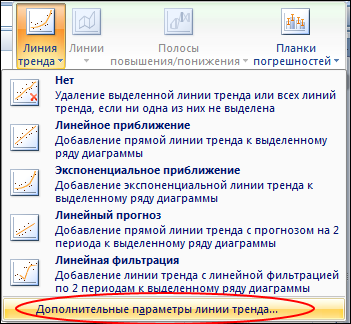
4. Из списка предложенных действий пострения линий тренда, выбираем Дополнительные параметры линии тренда .

5. В задании нам говорится:

2;
=> щелкнуть на кнопке ОК.

Устанавливаем настройки согласно запросу:

После выполнения этой операции график примет следующий вид:

Видео:Решение уравнений с помощью подбора параметра в Microsoft Office ExcelСкачать

Построение регрессионных моделей средствами Excel

ПОСТРОЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ средствами excel

Целью работы является изучение методов решения задач регрессионного анализа в Excel. Развитие навыков использования команды Сервис/Подбор параметра, встроенных статистических функций, построения линейных и нелинейных уравнений регрессии и линий тренда.

Пусть имеются ряды наблюдаемых величин t и у. Пусть ряд у представляет наблюдаемую величину продаж некоторым предприятием товара определенного вида за каждую неделю.

Значения элементов рядов представлены в табл.1.

Требуется построить линейную и нелинейную регрессионную модели yt=at+b, yt=b*exp(at). Параметры a и b подбираются так, чтобы минимизировать сумму квадратов разностей между наблюдаемым рядом y и теоретическими значениями yt, т. е. так, чтобы величина всех отклонений отвечала условию U=Σ(yi – ati – b)2 →min для i=1,2,3,…,n.

2.Последовательность выполнения задания

v Подготовим начальный рабочий лист с исходными данными как показано на рис.1.

Рис.1.

В диапазон ячеек А2:А9 введены значения из ряда t, в диапазон ячеек В2:В9 – значения ряда из табл.1. Под переменные a и b поиска решения отведены ячейки D2, Е2 соответственно. В ячейку F2 введена формула для минимизируемой функции цели:

=СУММКВРАЗН(B2:B9;E2+D2*A2:A9) (1)

В этой формуле использована функция СУММКВРАЗН(), вычисляющая сумму квадратов разностей соответствующих элементов двух массивов.

v Выберем команду Сервис/Поиск решения. Откроется диалоговое окно Поиск решения.

v Заполним диалоговое окно Поиск решения.

При заполнении окна Поиск решения введем абсолютную ссылку на ячейку с целевой функцией F2, в группе Равной выберем минимальному значению, так как требуется найти минимальное значение целевой функции, в поле Изменяя ячейки укажем диапазон ячеек D2:Е2.

v Далее установим параметры поиска решения, получим решение и далее повторим его с большей точностью и с меньшим допустимым отклонением и создадим отчет Excel по результатам (Рис.2.)

Microsoft Excel 12.0 Отчет по результатам

Рабочий лист: [работа3.xlsx]Лист1

Отчет создан: 07.04.2010 14:50:32

Целевая ячейка (Минимум)

v Найдем параметры а и b в линейной регрессионной модели с помощью статистических функций НАКЛОН() и ОТРЕЗОК(). Функция НАКЛОН() определяет коэффициент наклона линейного тренда. Ее формат записи – НАКЛОН( ; ), функция ОТРЕЗОК() определяет точку пересечения линейного тренда с осью ординат. Ее синтаксис – ОТРЕЗОК( ; ).

Аргументы этих функций:

– это массив значений независимой наблюдаемой величины. Если аргумент опущен, то по умолчанию полагается, что это массив из натурального ряда чисел того же ряда, как и аргумент ;

— это массив известных значений зависимой наблюдаемой величины.

=НАКЛОН(B2:B9;A2:A9) (2)

=ОТРЕЗОК(B2:B9;A2:A9) (3)

в ячейки D4 и Е4 соответственно и сравним результаты с содержимым ячеек D2 и Е2.

v Найдем параметры а и b линейной регрессионной модели, используя команду Добавить линию тренда. Для этого:

ü построим точечный график по данным диапазона ячеек А2:В9, выделим точки графика двойным щелчком, затем щелкнем на них правой кнопкой мыши. Раскроется контекстное меню, в нем выберем команду Добавить линию тренда;

ü в раскрывшемся диалоговом окне Линия тренда на вкладке Тип выберем Линейная, затем на вкладке Параметры установим флажки Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Щелкнем кнопку ОК. (Рис.3.)

Рис.4. Диаграмма с линией тренда типа Линейная

v Вычислим теоретическое значение наблюдаемой величины yt при t из ячейки А2. Для этого в ячейку С2 введем формулу:

Сравним результат с содержимым ячейки В2.

v Вычислим теоретическое значение yt при t из ячейки А4 с помощью функции ПРЕДСКАЗ(). Ее синтаксис — ПРЕДСКАЗ(ti; ; ). Аргумент ti — это точка данных из массива t, для которой предсказывается теоретическое значение yti. Теоретическое значение в ячейке С4 вычислим по формуле:

Буксировкой формулы (5) вниз заполним диапазон С5:С9 новыми yt.

Сравним значения в диапазонах В4:В12 и С4:С12.

v Вычислим значения уравнения линейной регрессии для целого диапазона значений независимой переменной с помощью функции ТЕНДЕНЦИЯ(). Ее синтаксис – ТЕНДЕНЦИЯ( ; ; ;[ ]).

Аргумент — это массив значений t, для которых функция ТЕНДЕНЦИЯ() возвращает соответствующие значения yt.

Новое значение зависимой переменной вычислим в ячейке В10 по формуле:

Буксировкой формулы (6) вниз заполним диапазон В11:В12 новыми значениями у.

v Найдем параметры а и b линейной регрессионной модели с помощью статистической функции ЛЕНЕЙН(). Эта функция возвращает массив значений параметров уравнения многомерной регрессии, для двумерной регрессии – параметры а и b. Ее синтаксис – ЛЕНЕЙН( ; ;[ ];[ ]), где — это логическое значение.

Введем в ячейки D6:Е6 формулу:

Результаты, полученные в диапазонах ячеек D2:Е2, D4:Е4, D6:Е6 и на диаграмме с линией тренда типа Линейная, сравним между собой.

v Построим нелинейную экспоненциальную модель. Она описывается уравнением yt=b*exp(a*t).

Значения параметров b, m степенной модели вида yt=b*m^t определяется с помощью функции ЛГРФПРИБЛ( ; ;[ ];[ ]), где — это логическое значение, которое указывает, требуется ли вывести дополнительную статистику по регрессии, например корреляции.

ü Для определения параметров нелинейной экспоненциальной модели в ячейки D8:Е8 введем формулу:

а в ячейку Е9 – формулу: LN(D8) (9)

ü Значения экспоненциального тренда предсказывает функция РОСТ. Для построения экспоненциального тренда в ячейку G2 введем формулу:

и отбуксируем ее на диапазон G3:G12.

ü вычислим теоретическое значение yt (нелин) наблюдаемой величины, используя экспоненциальную модель.

Для этого введем в ячейку F4 формулу:

Буксировкой формулы (11) заполним диапазон F5:F12 результатами вычислений. Сравним значения в ячейках B4:B12, С4:С12, F4:F12, G4:G12.

ü Построим точечный график «Динамика продажи» по данным диапазона ячеек А2:В9, затем, используя команду Добавить линию тренда, построим экспоненциального типа линию тренда (описание выше).Рис.5.

Рис.5. График с линией тренда типа Экспоненциальная

ü Сравним между собой линейную и экспоненциальную модели по коэффициенту корреляции. Коэффициент корреляции в линейной и экспоненциальной модели различается на 0,042 (R2лин > R2экс).

ü Результаты решения задания представлены на Рис.6.

Построение полиномиальной регрессионной модели.

Требуется построить полиномиальные модели различных степеней вида

и сравнить оценки их погрешностей. Определение коэффициентов таких уравнений осуществить средством Поиск решения.

v Подготовим начальный рабочий лист кА показано на рис.7. Заданные ряды Y и t помещены в диапазоны С7:С16 и А7:А16 соответственно. В диапазонах С7:С16, D7:D16, E7:E16 будем отображать квадраты погрешности между фактическим значением Yi и полученным из полиномов второй, третьей и четвертой степени уравнений регрессии соответственно.

v Введем следующие формулы:

v Cкопируем эти формулы в диапазон С8:С15, D8:D15, E8:E15 соответственно. Полученные результаты сравним между собой ряды квадратов погрешностей полиномов.

v В ячейке С16 вычислим сумму квадратов погрешностей для приближения полиномом 2-й степени, введя формулу:

С17 = СУММ (С7:С16) (15)

Скопируем эту формулу методом буксировки вправо на диапазон D17:Е17, чтобы вычислить сумму квадратов погрешностей приближений полиномами 3-й и 4-й степени. Сравним результаты в ячейках С17:Е17 между собой.

v Для вычисления коэффициентов а, b, c полинома второй степени выберем команду Сервис/Поиск решения. В диалоговом окне Сервис/Поиск решения установим целевую ячейку С17, в поле Равной установим минимальному значению, в поле Изменяя ячейки – диапазон B3:D3. После щелчка Выполнить, результаты поиска – значения коэффициентов а, b, с появляются в ячейках B3:D3.

v Аналогично предыдущему пункту, используя средство Поиск решения, определим коэффициенты а, b, c, d в ячейках В4:Е4 для приближения полиномом 3-й степени, затем то же самое для приближения полиномом 4-й степени в ячейках В5:F5 определим коэффициенты а, b, c, d, e.

v Сделаем нелинейный регрессионный анализ, используя средства деловой графики Excel, не прибегая к вычислениям, сначала для модели 2-й степени. Для этого построим график Y(t), используя ряды t и Y в ячейках А7:А16, В7:В16. Затем кликнув щелчком на этом графике правой кнопкой мыши и в появившемся контекстном меню выберем пункт Добавить линию тренда. В появившемся окне Линия тренда, в котором выберем тип уравнения аппроксимации Полиномиальная и его степень; на вкладке Параметры установим флажки Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации. Будет выведен график уравнения регрессии и само уравнение с числовыми значениями коэффициентов и квадрат коэффициента корреляции R^2.

v Аналогично выполним графическое построение линий тренда для полиномов 3-й, 4-й степеней с показом уравнений на графике. Сравним регрессионные модели полиномами

Результаты решения показаны на рис.8.

В данной работе я изучила метод решения задач регрессионного анализа в Excel. Развила навыки использования команды Сервис/Подбор параметра, встроенных статистических функций, построения линейных и нелинейных уравнений регрессии и линий тренда.

С помощью команды Сервис/ Подбор параметра, функций НАКЛОН(), ОТРЕЗОК() и ЛИНЕЙН() я разными способами рассчитала значения а и b линейной регрессионной модели. Затем сравнила полученные значения, и они получились одинаковыми. По полученным данным я построила диаграмму с линией тренда типа Линейная. Также вычислила теоретическое значение yt при t с помощью функции ПРЕДСКАЗ() и новые значения у с помощью функции ТЕНДЕНЦИЯ().

Для определения параметров нелинейной экспоненциальной модели использовала формулу ЛГРФПРИБЛ, LN. Для построения экспоненциального тренда – функцию РОСТ. Затем вычислила теоретические значения yt (нелин) наблюдаемой величины, используя экспоненциальную модель и построила диаграмму с линией тренда типа Экспоненциальная.

Коэффициент корреляции в линейной и экспоненциальной модели различается на 0,0303 (R2лин > R2экс).

Во второй части данной работы я построила полиномиальные модели различных степеней. Для этого были использованы формулы . Для вычисления коэффициентов а, b, c полинома различных степеней использовала команду Сервис/Поиск решения. По полученным данным построила график Excel для модели 2-й, 3-й, 4-й степени. Сравнивая оценки погрешностей полиномонов 2-й, 3-й, 4-й степеней можно сделать вывод, что погрешность уменьшается с увеличением степени, особенно это наглядно представлено из вычисленных сумм квадратов разностей.