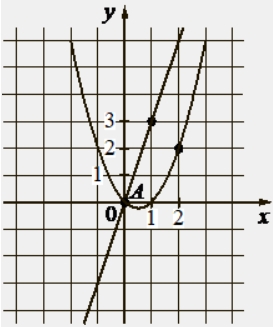
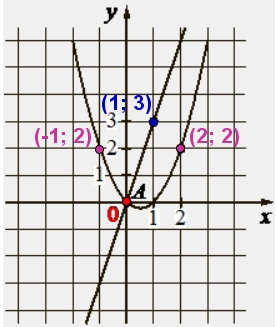
На рисунке изображены графики уравнений x2 y2 25

На рисунке изображены графики функций видов f(x) = ax 2 + bx + c и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.

Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0 .
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ax 2 + bx + c): (–1; 2) – в 1-е уравнение , (2; 2) – во 2-е уравнение, и с = 0 в оба уравнения, получим систему из двух уравнений:

begin 2 = acdot (-1)^ + bcdot (-1) + 0 \ 2 = acdot 2^ + bcdot 2 + 0 end\begin 2 = a – b \ 2 = 4a + 2b color |:2end\begin 2 = a – b \ 1 = 2a + b end

Cложим уравнения:

2 + 1 = а + 2а – b + b
3 = 3a
a = 3/3 = 1

Подставим а = 1 во первое уравнение системы, найдём b:

2 = 1 – b
2 – 1 = –b
1 = –b
b = –1

Функция параболы имеет вид:

Подставим точку (1; 3) принадлежащую прямой в функцию g(x) = kx и найдём k:

3 = k·1
k = 3

Функция прямой имеет вид:

Найдём координаты абсцисс точек пересечения функций:

Видео:На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.Скачать

Презентация «Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Добрый день, уважаемые коллеги! Приятно видеть вас в этой аудитории, и очень надеюсь, что сегодня у нас с вами получится интересное и полезное мероприятие.

Мастер-класс
учителя математики
МОУ «СОШ№ 14»
Рискуловой Тотайхан Оразалиевны
по теме:
«Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
а Эдельбай
Благодарненский район

«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому, и я научусь»

Конфуций
Конфуций-древнекитайский проповедник,
писатель, философ.

Сложно подготовить обучающихся к сдаче экзамена. Это большой труд. Но не надо бояться. Если вы хорошо знаете, объясняете, любите свой предмет и своих учеников, вы обязательно сможете подготовить их к ЕГЭ по математике.
Важный принцип — это логичность. В шутливой манере он говорит: «нормальные герои всегда идут в обход». Нужно учиться использовать наличный запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для ответа наиболее простым и понятным способом.
Главная заповедь учителя – заметить даже самое маленькое продвижение ученика вперёд и поддержать его успех.

Цель мастер-класса:
показать приемы решения нового 9 задания по теме «Анализ графиков»
развивать логическое мышление, память, познавательный интерес

1 9 задание
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
2
Решение
Уравнение прямой у=kx+b. Первая прямая проходит
через точки (-4;1) и (-2;4), k= 𝟑 𝟐 .
Найдем b,подставив координаты одной из точек в уравнение
1=1,5·(-4)+ b, b=7.
у=1,5х+7-уравнение1 прямой.
2) Вторая прямая проходит через точки (-1;0) и (2;3), k= 𝟑 𝟑 =𝟏.
Найдем b,подставив координаты одной из точек в уравнение
0=1·(-1)+ b, b=1.Тогда у=х+1-уравнение2 прямой.
3)Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 Вычтем из 1 уравнения 2 уравнение , получим 0=0,5х+6.Отсюда х=-12.Тогда у=-11.
Ответ:-11

9 задание
На рисунке изображен график функции f(x)= 𝒂 x²+bx+c,где числа a,b и c-целые. Найдите значение f(-12).
Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m= -4,n= -3, 𝒂 =1.
f(x)=(x-(-4))²+(-3),
f(x)=(x+4)²-3,
f(-12)=(-12+4)²-3,
f(-12)=61.
Ответ:61
2

9 задание
На рисунке изображен график функции f(x)= 𝒙 𝟐 𝒂 +bx+c, где числа 𝒂 ,b и c-целые. Найдите значение f(4).
Решение.
f(x)= 𝟏 𝒂 (x-m)²+n,где (m, n)-координаты вершины параболы.
По графику m= -2,n= 11, 𝒂 = -2. (Введем новую систему координат через вершину параболы, тогда график
функции f(x)= 𝒙 𝟐 𝒂 проходит через точку (2;-2).
Подставив в формулу f(x)= 𝒙 𝟐 𝒂 ,найдем а)
f(x)= — 𝟏 𝟐 (x+2)²+11= — 𝟏 𝟐 x²-2x+9,значит, 𝒂 = — 2, b=-2, c=9.
Тогда f(4)= — (𝟒+𝟐)² 𝟐 +11= — 18+11= — 7.
Ответ:- 7

9 задание. На рисунке изображен график функции f(x)= 𝒂 x²+bx+c. Найдите f(-1).
Решение.
Из рисунка видно, что график проходит через (3;2);(4;5);(5;4)
9а+3b+c= 2, 16a+4b+c=𝟓, 25a+5b+c=4.
Вычтем из 2 уравнения 1-е,
получим7a+b=𝟑
Вычтем из 3уравнения 2-е,
получим 9a+b=-𝟏
Решив систему уравнений 7a+b=𝟑, 9a+b=−1;
находим 𝒂=-2 ,b=17.
Тогда f(x)=- 2 x²+17x+c и f(3)=2, найдем ,что с=-31.
f(x)=- 2 x²+17x-31,
f(-1)=-2-17-31=-50
Ответ:-50
4

9 задание. На рисунке изображен график функции f(x)=ах²+bx+c,где числа 𝒂 ,b и c-целые. Найдите абсциссу вершины параболы.
Решение.
Абсцисса вершины параболы найдем по формуле х 𝟎 = — 𝒃 𝟐𝒂
Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда
9а−3b+c= −2, 4a−2b+c=1, a−b+c=6 ;
вычтем из 1 уравнения 2-е, получим5a-b=-𝟑
вычтем из 2 уравнения 3-е,получим 3a-b=-𝟓.
Решив систему уравнений 5a−b=−𝟑, 3a−b=−𝟓; находим 𝒂=1 ,b=8.
Абсцисса вершины параболы х 𝟎 = — 𝒃 𝟐𝒂 =-4.
Ответ:-4

7
9 задание. На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B

Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).
Подставим координаты точки (-1;-3), получим
-3=а- b-3.Отсюда а=b.
g(x)= ах²+аx-3.
Подставим координаты точки (2;3), получим, что а=1.
g(x)= х²+x-3.
Чтобы найти абсциссу точки ,нужно решить уравнение х²+x-3=5х+9,
х²-4x-12=0.
По теореме Виета х 𝟏 ·х 𝟐 =-12, х 𝟏 + х 𝟐 =4
По графику х 𝟏 =-2, тогда х 𝟐 =6.
Ответ:6

Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m=-3,n=3, 𝒂 =1.
f(x)=(x-(-3))²+3
f(x)=(x+3)²+3,
f(x)=х²+6х+12, так как f(x)=0.
то х²+6х+12=0
D=6²-4·1·12= -12.
Ответ:-12
Решите 9 задание
На рисунке изображен график функции f(x)= 𝒂x²+bx+c,где числа 𝒂 ,b и c-целые. Найдите значение дискриминанта уравнения f(x)=0.
8

Решение.
|bx+c|=0 в точке излома. Значит, bx+c=0 при х=2.

9 задание
На рисунке изображен график функции вида 𝒇 𝒙 = 𝒂 x+|bx+c|+d, где числа 𝒂,b, c и d-целые.
Найдите корень уравнения bx+c=0

9 задание.
На рисунке изображён график функции вида f(x)=ax + |bx + c| +d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.

Решение.
|bx + c|=0 в точке излома при х=1,
Если х 1,то f(x)=ax +bx + c +d=(а+b)х+с+ d, где а+b-угловой коэффициент, по графику а+b=2.
Продолжив прямую до пересечения с осью Оу, получим , что с+ d =-1.

Решив эти системы а−b=−4 а+b=𝟐 и с+ d =−1 d−с=5 , получим,что
a=-1;b=3;c=-3;d=2. Подставив найденные значения в уравнение ax +d=0 , получим -x + 2=0,
х=2.
Ответ:2

11 На рисунке изображен график функции вида f(x)= 𝒂 cos(bπx+c)+d, где числа 𝒂,b, c и d-целые. Найдите 𝒇 𝟏𝟎𝟎 𝟑 .
Решение.
По графику 𝒇 𝒎𝒂𝒙 =𝟏,𝒇 𝒎𝒊𝒏 =-3
d= 𝒇 𝒎𝒂𝒙 + 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏−𝟑 𝟐 = -1. |a|= 𝒇 𝒎𝒂𝒙 − 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏+𝟑 𝟐 =2.
По графику 𝒂 =2, c=0, T=2
T= 𝟐𝝅 𝒃𝝅 = 𝟐 𝒃 , то есть 𝟐 𝒃 =2, отсюда b=1
f(x)=2cosπx-1,
f 𝟏𝟎𝟎 𝟑 =f 𝟗𝟔 𝟑 + 𝟒 𝟑 =𝒇 𝟑𝟐+ 𝟒 𝟑 =f 𝟒 𝟑 ,
f 𝟒 𝟑 =2cosπ· 𝟒 𝟑 -1 = 2cos 𝟒 𝟑 π-1 = 2cos π+ π 𝟑 -1= -2cos π 𝟑 −1= -2.
Ответ:-2

9 задание. На рисунке изображен график функции f(x)=k х. Найдите f(2,56)
Решение.
График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим
-3=k 𝟒 ,
2k=-3,
k =-1,5.
f(2,56)=-1,5 𝟐,𝟓𝟔 =−1,5·1,6=−2,4.

9 задание. На рисунке изображен график функции f(x)= 𝒌 𝒙 +a. Найдите f (0,25)

Решение. График функции имеет горизонтальную асимптоту y=-2, значит, а=-2.
(График функции f(x)= 𝒌 𝒙 +a получается сдвигом графика функции f(x)= 𝒌 𝒙 вдоль оси Оу на величину |а| вверх, если а>0 и вниз если a 0 и вправо если a 0 и вниз если b 0 и вправо если b

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 861 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 51 человек из 23 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:На рисунке изображены графики функций вида у=ах^2+вх+ с.Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 136 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 20.10.2021
• 347
• 6

• 20.10.2021
• 1347
• 16

• 20.10.2021
• 74
• 0

• 20.10.2021
• 182
• 2

• 20.10.2021
• 257
• 1

• 20.10.2021
• 202
• 2

• 20.10.2021
• 181
• 0

• 20.10.2021
• 240
• 0

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.10.2021 16820
• PPTX 5.1 мбайт
• 1380 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Рискулова Тотайхан Оразалиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 35002
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:На рис. изображены графики f(x)=2x^2-5x+4 и g(x)=ax^2+bx+c, кот. пересекаются в точках А и В.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

В Госдуме предложили унифицировать школьные программы

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Онлайн-конференция о профессиональном имидже педагога

Время чтения: 2 минуты

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:На рис. изображены графики функций f(x)=-3x+13 и g(x)=ax^2+bx+c, кот. пересекаются в точках А и В.Скачать

Задание 9 ЕГЭ по математике. Графики функций

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №9 ЕГЭ.

Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 9 в формате ЕГЭ-2021

Линейная функция

1. На рисунке изображён график функции . Найдите значение , при котором

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

Вычтем из первого уравнения второе:

Уравнение прямой имеет вид:

Найдем, при каком значение функции равно -13,5.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции

Вычтем из первого уравнения второе.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен

Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой

Для точки пересечения прямых:

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть

5. На рисунке изображен график функции . Найдите с.

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид .

6. На рисунке изображён график функции Найдите

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

Формула функции имеет вид:

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому

График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

Найдем абсциссу точки B. Для точек A и B:

(это абсцисса точки A) или (это абсцисса точки B).

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

График функции проходит через точку (2; 1); значит,

График функции проходит через точки (2; 1) и (1; -4), — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда

Для точек A и B имеем:

Отсюда (абсцисса точки A) или (абсцисса точки B).

9. На рисунке изображён график функции . Найдите f (6,76).

Функция задана формулой:

Ее график проходит через точку (4; 5); значит,

10. На рисунке изображен график функции . Найдите .

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда =5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:

Поделим второе уравнение на первое:

Подставим во второе уравнение:

12. На рисунке изображен график функции . Найдите

График функции проходит через точку Это значит, что

формула функции имеет вид: .

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

Вычтем из второго уравнения первое:

или — не подходит, так как (как основание логарифма).

14. На рисунке изображен график функции .

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на .

16. На рисунке изображён график функции

На рисунке — график функции Так как

График функции проходит через точку A Подставим и координаты точки А в формулу функции.

Так как получим:

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 9 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

🎬 Видео

На рисунке изображены графики функций вида y=ax^2+bx+c ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.Скачать

[ОГЭ] На рисунках изображены графики функций вида у = кх + ЬСкачать

На рисунке изображены графики функций вида y=kx+b ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

Графики функций f(x)=5x+9 и g(x)=ax^2+bx+c пересекаются в точках A и B. Найдите абсциссу точки B.Скачать

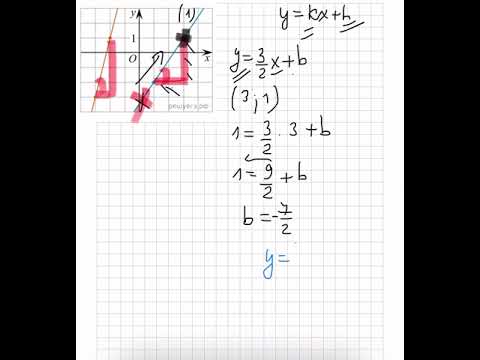
Как найти абсциссу точки пересечения двух прямых?Скачать

На рисунке изображены графики функций вида y=kx+b ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

На рисунке изображены графики функций f(x)=a √x и g(x)=kx+bСкачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

8246Скачать

На рисунке изображены графики функций 2Скачать

На рисунках изображены графики вида у=кх+вСкачать

На рис. изображены графики функций f(x)=k/x и g(x)=ax+b, кот. перес. в т-ках А(−2; −3) и В(𝑥0; 𝑦0).Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Реальный ЕГЭ-2023, задача 10. На рисунке изображены графики функций 𝑓(𝑥)=𝑎 корней из 𝑥 и 𝑔(𝑥)=𝑘𝑥+𝑏.Скачать

На рисунке изображены графики функций ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать