Про уравнения - легко » Статьи

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Обновлено
Задача 54852 Центр окружности,касающейся.
Содержание
  1. Условие
  2. Решение
  3. На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
  4. 9 класс. Геометрия. Метод координат. Уравнение окружности.
  5. 9 класс. Геометрия. Метод координат. Уравнение окружности.
  6. Вопросы
  7. Поделись с друзьями
  8. Комментарии преподавателя
  9. Решение задач
  10. Заключение
  11. № 28*. Составьте уравнение окружности с центром в точке (1;2), касающейся оси х.
  12. 🌟 Видео

Условие

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Центр окружности,касающейся осей
координат,
лежит на
прямой 3x-5y+15=0. Найти
уравнение окружности.

Решение

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

(x-x_(o))^2+(y-y_(o))^2=r^2 — уравнение окружности с центром в точке С (x_(o);y_(o))

Есть два условия в задаче:

!)
центр С (x_(o);y_(o)) лежит на прямой
3x-5y+15=0 ⇒ y=(3x+15)/5

Окружность касается осей координат,
значит расстояния от центра окружности до осей координат равны [i]радиусу[/i] окружности
С (|r|;r)

( По рисунку видно, что окружность может располагаться только в верхней полуплоскости)

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.

Пусть (a; 0) — координаты точки касания окружности с осью Ox. Тогда (см. рисунок) точка касания окружности с осью Oy имеет координаты (0; a), центр окружности имеет координаты (a; a) и радиус окружности равен a, поскольку окружность проходит через точку A(2; 1), у которой каждая координата больше нуля. Это означает, что окружность расположена в I квадранте, в котором a > 0.

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Следовательно, уравнение окружности имеет вид (x — a) 2 + (y — a) 2 = a 2 .

Так как окружность проходит через точку A(2; 1), то имеем (2 — a) 2 + (1 — a) 2 = a 2 , откуда a = 1 или a = 5.

Искомое уравнение окружности: (x — 1) 2 + (y — 1) 2 = 1 или (x — 5) 2 + (y — 5) 2 = 25.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).

9 класс. Геометрия. Метод координат. Уравнение окружности.

9 класс. Геометрия. Метод координат. Уравнение окружности.

  • Оглавление
  • Занятия
  • Обсуждение
  • О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Уравнение окружности (1)Скачать

Уравнение окружности (1)

Решение задач

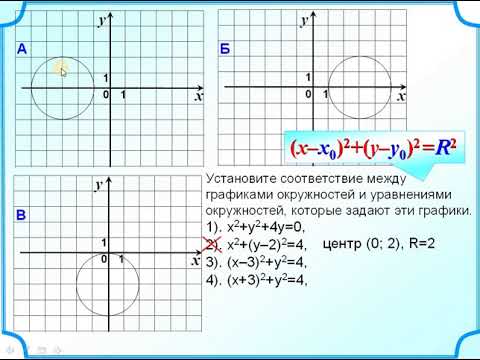
Вы­яс­ни­те, какие из дан­ных урав­не­ний яв­ля­ют­ся урав­не­ни­я­ми окруж­но­сти.

Най­ди­те ко­ор­ди­на­ты цен­тра и ра­ди­ус каж­дой окруж­но­сти.

а) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

б) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

в) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

г) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности;

д) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рас­смот­рим каж­дое урав­не­ние в от­дель­но­сти.

а) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности– окруж­ность, На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

б) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности– окруж­ность, На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

в) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
Вы­де­лим пол­ный квад­рат:
На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиурав­не­ние не яв­ля­ет­ся урав­не­ни­ем окруж­но­сти.

г) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности.
Вы­де­лим пол­ный квад­рат:
На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности– окруж­ность, На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

д) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
Вы­де­лим пол­ный квад­рат:
На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности– окруж­ность, На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На окруж­но­сти, за­дан­ной урав­не­ни­ем На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности, най­ди­те точки

а) с абс­цис­сой –4; б) с ор­ди­на­той 3.

Ре­ше­ние: по­стро­им окруж­ность с цен­тром (0;0) ра­ди­у­са 5 (рис. 1).

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 1. Ил­лю­стра­ция к за­да­че

а) Ко­ор­ди­на­ты точек окруж­но­сти с абс­цис­сой –4 яв­ля­ют­ся ре­ше­ни­я­ми си­сте­мы:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

По­лу­ча­ем точку На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностии точку На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 2. Ил­лю­стра­ция к за­да­че

б) Ко­ор­ди­на­ты точек окруж­но­сти с ор­ди­на­той 3 яв­ля­ют­ся ре­ше­ни­я­ми си­сте­мы:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 3. Ил­лю­стра­ция к за­да­че

По­лу­ча­ем точку На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностии ту же самую точку На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности.

За­пи­ши­те урав­не­ние окруж­но­сти ра­ди­у­са r с цен­тром в точке А, если

а) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

б) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

в) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

г) На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

а) Окруж­ность На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

б) Окруж­ность На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности.
Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

в) Окруж­ностьНа рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

г) Окруж­ностьНа рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности
Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На­пи­ши­те урав­не­ние окруж­но­сти с цен­тром в на­ча­ле ко­ор­ди­нат, про­хо­дя­щей через точку
На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 4. Ил­лю­стра­ция к за­да­че

Най­дем ра­ди­ус, как рас­сто­я­ние ОВ:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

За­пи­шем урав­не­ние окруж­но­сти с цен­тром О(0;0):

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Для кон­тро­ля про­ве­рим, удо­вле­тво­ря­ют ли по­лу­чен­но­му урав­не­нию ко­ор­ди­на­ты точки В:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностизна­чит, точка В лежит на окруж­но­сти.

Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На­пи­ши­те урав­не­ние окруж­но­сти, про­хо­дя­щей через точку А(1;3), если из­вест­но, что центр окруж­но­сти лежит на оси абс­цисс, а ра­ди­ус равен 5.

Сколь­ко су­ще­ству­ет таких окруж­но­стей?

Дано: А(1;3) – точка окруж­но­сти,

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Найти: урав­не­ние окруж­но­сти (С; r=5).

Ре­ше­ние: центр ис­ко­мой окруж­но­сти уда­лен от точки А(1;3) на рас­сто­я­ние 5, зна­чит, он лежит на окруж­но­сти с цен­тром в точке А(1;3) ра­ди­у­са 5, но он еще лежит и на оси Ох. По­стро­им окруж­ность (А(1;3); r=5) (рис. 5).

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 5. Ил­лю­стра­ция к за­да­че

Точек, удо­вле­тво­ря­ю­щих нашим усло­ви­ям, на оси Ох две: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Для опре­де­ле­ния ко­ор­ди­нат этих точек со­ста­вим си­сте­му:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

За­пи­шем урав­не­ния ис­ко­мых окруж­но­стей:

окруж­ность ( На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

окруж­ность ( На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностии по­стро­им эти окруж­но­сти (рис. 6):

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 6. Ил­лю­стра­ция к за­да­че

Ответ: две окруж­но­сти.

На­пи­ши­те урав­не­ние окруж­но­сти, про­хо­дя­щей через две за­дан­ные точки На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностии В(0;9), если из­вест­но, что центр окруж­но­сти лежит на оси ор­ди­нат.

Дано: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиокруж­но­сти На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности;

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиoкруж­но­сти На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности.

за­пи­сать урав­не­ние окруж­но­сти.

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 7. Ил­лю­стра­ция к за­да­че

За­пи­шем урав­не­ние окруж­но­сти На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружноститак как окруж­ность про­хо­дит через точки А и В, то их ко­ор­ди­на­ты удо­вле­тво­ря­ют урав­не­нию окруж­но­сти:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Под­ста­вим най­ден­ные зна­че­ния в урав­не­ние.

Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На­пи­ши­те урав­не­ние окруж­но­сти с цен­тром в точке А(6;0), про­хо­дя­щей через точку В(-3;2).

Дано: А(6;0) – центр,

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиокруж­но­сти.

Найти: урав­не­ние окруж­но­сти.

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Рис. 8. Ил­лю­стра­ция к за­да­че

На­хо­дим ра­ди­ус как рас­сто­я­ние АВ:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

За­пи­шем урав­не­ние окруж­но­сти:

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Ответ: На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

9 класс, 6 урок, Уравнение окружности

Заключение

Итак, мы рас­смот­ре­ли серию задач по теме «Окруж­ность» и в каж­дой за­да­че ис­поль­зо­ва­ли урав­не­ние окруж­но­сти.

На сле­ду­ю­щем уроке мы вы­ве­дем урав­не­ние пря­мой.

Видео:Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Уравнение окружности ? Окружность в системе координат / Функция окружности

№ 28*. Составьте уравнение окружности с центром в точке (1;2), касающейся оси х.

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Заменим уравнение окружности с центром

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиНа рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

где R — радиус окружности. Уравнение оси х: у

= 0. Окружность и ось х касаются, значит, система уравнений

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

имеет единственное решение. Решим систему. 1)

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружностиНа рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

Система будет иметь единственное решение (а; 0), если данное уравнение будет иметь один корень х = а, то есть если D = 0 или

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

то есть R=2, так как R>0. А значит

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности— уравнение искомой окружности.

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности

На рис 22 окружность с центром в точке a касается осей координат напишите уравнение окружности Решебник по геометрии за 8 класс (А.В. Погорелов, 2001 год),
задача №28
к главе «§8. Декартовы координаты на плоскости».

🌟 Видео

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямой

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известно

Найти центр и радиус окружностиСкачать

Найти центр и радиус окружности

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),

№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2Скачать

№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.

Составляем уравнение окружностиСкачать

Составляем уравнение окружности

№965. Напишите уравнения окружностей с центром в начале координат и радиусами r1=3, r2= √2 , r3=5/2.Скачать

№965. Напишите уравнения окружностей с центром в начале координат и радиусами r1=3, r2= √2 , r3=5/2.

ОГЭ Задание 11 Уравнение окружностиСкачать

ОГЭ Задание 11 Уравнение окружности

8 класс. Геометрия. Уравнение окружности.Скачать

8 класс. Геометрия. Уравнение окружности.

Уравнение окружностиСкачать

Уравнение окружности

№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известно
Поделиться или сохранить к себе: