Вопрос по алгебре:
На координатной плоскости отмечены точки с и д.
Какое уравнение задает прямую, проходящую через эти точки?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- На координатной плоскости отмечены точки с и д какое уравнение задает прямую d 3 15
- На координатной плоскости заданные точки M(3 ; — 1) и N(5 ; 3)?
- Каким уравнением задается прямая проходящая через точки А(7 ; 19) В(9 ; 15)?
- 1. На плоскости заданы две точки : A(2 ; 3), B( — 7 ; 6)?
- Напишите уравнения прямой, проходящей через заданные точки : 1)А(1 ; 0), В(0 ; 1)?
- Составьте уравнений прямой, проходящей через заданные две точки : А(2 : 3) В( — 6 : — 1)?
- График прямой пропорциональности проходит через точку (3 : — 12) на координатной плоскости XOY?
- Решение ?
- Составьте уравнение прямой , проходящей через заданные две точки : А(0, 3) В( — 1, 0)?
- Составьте уравнение прямой проходящей через заданные две точки : А(0 ; 3, В( — 1 ; 0)?
- На рисунке изображен фрагмент координатной плоскости каким уравнением задается прямая CD?
- Каким уравнением задается прямая проходящая через точки А (7 ; 19) и B (9 : 15)?
- Расстояние между двумя точками онлайн
- Предупреждение
- Расстояние между двумя точками на прямой
- Расстояние между двумя точками на плоскости
- Расстояние между двумя точками в пространстве
- 💥 Видео
Ответы и объяснения 1
Попробуем подставить координаты точки С в данные уравнения, и проверить, какие из них дадут правильные равенства.
Эта проверка показывает, что через точку С проходят прямые, описываемые вторым и третьим уравнениями.
Попробуем подставить в эти два уравнения координаты точки Д. Правильное равенство образуется только в третьем уравнении.
Следовательно, уравнение прямой, которая проходит через точки С и Д — .
Ответ: №3.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

На координатной плоскости отмечены точки с и д какое уравнение задает прямую d 3 15
Ответ: 1 способ: Уравнение прямой у=kx + b.
Даны координаты двух точек. Подставить координаты в уравнение у = kx + b и получить два уравнения относительно переменных k и b. Решить систему.
2 способ: Подставлять координаты этих двух точек в каждое уравнение (обе должны давать верные равенства одновременно)
Видео:Как отмечать дроби на координатной прямойСкачать

На координатной плоскости заданные точки M(3 ; — 1) и N(5 ; 3)?
Алгебра | 5 — 9 классы
На координатной плоскости заданные точки M(3 ; — 1) и N(5 ; 3).
Какое уравнение задает прямую , проходящую через эти точки?
Уравнениепрямой y = kx + b
M(3 ; — 1)3k + b = — 1, b = — 1 — 3k
b = — 1 — 3 * 2 = — 7
получилиуравнениеy = 2x — 7.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Каким уравнением задается прямая проходящая через точки А(7 ; 19) В(9 ; 15)?
Каким уравнением задается прямая проходящая через точки А(7 ; 19) В(9 ; 15).
Видео:Изображение обыкновенных дробей на координатном луче. 5 класс.Скачать

1. На плоскости заданы две точки : A(2 ; 3), B( — 7 ; 6)?
1. На плоскости заданы две точки : A(2 ; 3), B( — 7 ; 6).
А) Определить расстояние между данными точками ; б) найти уравнение прямой, проходящей через точки А и В.
2. Дано уравнение прямой y = 2x – 4 и точка А(4 ; — 2).
Найти уравнение прямой, проходящей через точку А перпендикулярно к данной прямой.
Видео:Видеоурок "Координатная плоскость, координата точки"Скачать
Напишите уравнения прямой, проходящей через заданные точки : 1)А(1 ; 0), В(0 ; 1)?
Напишите уравнения прямой, проходящей через заданные точки : 1)А(1 ; 0), В(0 ; 1).
Видео:ОГЭ по математике. Задание 7Скачать

Составьте уравнений прямой, проходящей через заданные две точки : А(2 : 3) В( — 6 : — 1)?
Составьте уравнений прямой, проходящей через заданные две точки : А(2 : 3) В( — 6 : — 1).
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

График прямой пропорциональности проходит через точку (3 : — 12) на координатной плоскости XOY?
График прямой пропорциональности проходит через точку (3 : — 12) на координатной плоскости XOY.
Каким уравнение задается эта прямая.
Видео:Составляем уравнение прямой по точкамСкачать

Решение ?
График прямой пропорциональности проходит через точку ( — 3 ; 9)на координатной плоскости х0у.
Каким уравнением задается эта прямая пропорциональность?
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Составьте уравнение прямой , проходящей через заданные две точки : А(0, 3) В( — 1, 0)?
Составьте уравнение прямой , проходящей через заданные две точки : А(0, 3) В( — 1, 0).
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Составьте уравнение прямой проходящей через заданные две точки : А(0 ; 3, В( — 1 ; 0)?
Составьте уравнение прямой проходящей через заданные две точки : А(0 ; 3, В( — 1 ; 0).
Видео:11. Прямая в пространстве и ее уравненияСкачать

На рисунке изображен фрагмент координатной плоскости каким уравнением задается прямая CD?
На рисунке изображен фрагмент координатной плоскости каким уравнением задается прямая CD.
Видео:Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Каким уравнением задается прямая проходящая через точки А (7 ; 19) и B (9 : 15)?
Каким уравнением задается прямая проходящая через точки А (7 ; 19) и B (9 : 15).
Вопрос На координатной плоскости заданные точки M(3 ; — 1) и N(5 ; 3)?, расположенный на этой странице сайта, относится к категории Алгебра и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
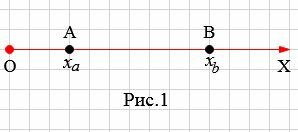 |
Расстояние между точками A и В равно:
| ( small AB=OB-OA. ) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| ( small AB=x_b-x_a . ) | (2) |
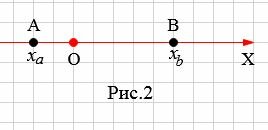 |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
| ( small AB=OB+OA. ) | (3) |
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
| ( small AB=x_b+|x_a|=x_b-x_a . ) | (4) |
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
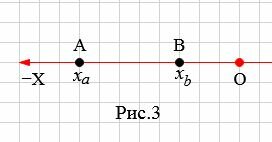 |
B этом случае рассояние между точками A и B равно:
| ( small AB=OA-OB. ) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| ( small AB=|x_a|-|x_b|=x_b-x_a . ) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| ( small AB=|x_b-x_a|= |x_a-x_b| . ) | (7) |
Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
| ( small AB=|x_b-x_a|= |7-(-4)|=11 . ) | (7) |
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
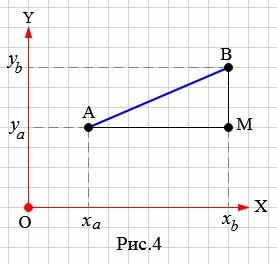 |
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
| ( small AM=x_b-x_a,;; BM=y_b-y_a. ) | (8) |
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
| ( small AB^2=AM^2+BM^2. ) |
Тогда, учитывая (8), получим:
| ( small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. ) |
| ( small AB=sqrt . ) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
 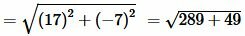 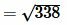 , , |
 . . |
Ответ: 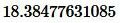
Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
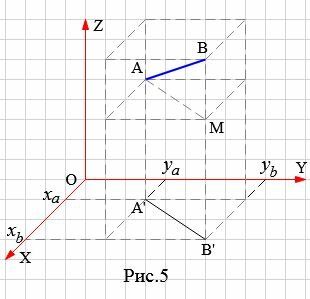 |
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
| ( small AB^2=AM^2+BM^2. ) | (10) |
Учитывая, что BM равно разности третьих координат точек B и A, получим:
| ( small BM=z_b-z_a. ) |
Из предыдующего параграфа следует, что:
| ( small A’B’^2=(x_b-x_a)^2+(y_b-y_a)^2. ) | (11) |
Но AM=A’B’. Тогда из (10) и (11) следует:
| ( small AB^2=AM^2+BM^2=A’B’^2+BM^2 ) ( small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. ) |
| ( small AB= sqrt. ) | (12) |
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
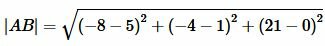 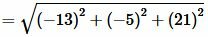 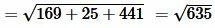 , , |
 . . |
Ответ: 
💥 Видео
КООРДИНАТНАЯ ПРЯМАЯСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой на плоскости. Решение задачСкачать








