На каком из указанных отрезков уравнение имеет действительный корень

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Дифференциальное исчисление функции одной переменной

Пределы

1.1. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

1.2. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

1.3. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

Рис. 1.1

1.4. Укажите ВСЕ утверждения, справедливые для графика функции, изображенного на рис.1.2:

Рис. 1.2

1.5. Если 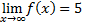, то равен

а) 3; б) -3; в) 0; г) ∞; д) не существует.

1.6. Если , то равен

а) 3; б) -3; в) 0; г) ∞; д) не существует.

1.7. Если , то равен

а) 3; б) -3; в) 0; г) ∞; д) не существует.

1.8. Если , и – чётная ,то равен

а) 3; б) -3; в) 0; г) ∞; д) не существует.

1.9. Вычислить .

а) 1; б) -1; в) 0; г) ∞; д) не существует.

1.10. Вычислить .

а) 1; б) -1; в) 0; г) ∞; д) не существует.

1.11. Вычислить .

а) 1; б) -1; в) 0; г) ∞; д) не существует.

1.12. Дано . Укажите ВСЕ верные утверждения:

– ограничена в окрестности точки ;

– бесконечно большая при ;

1.12. Дано П т /( * ) = 1 ООО ООО ООО. Укажите ВСЕверные утверждения:

^ *->2

а )/ (х) ограничена в окрестности точки х= 2 ;

б) / (х) — бесконечно большая при х —» 2 ;

а) а(х) и р(х) эквивалентны; б) а(х) более высокого порядка малости, чем Р(х);

в) а(х) более низкого порядка малости, чем Р(х); г) а(х) и р(х) одного порядка малости.

1.14. Известно, что прих—» Хо бесконечно малые а(х)и Р(х) эквива­ лентны (а(х)

Р(х)), Какое из следующих утверждений вернопри х —> х0?

а) а(х) более высокого порядка малости, чем Р(х); б) а(х) более низкого порядка малости, чем Р(х); в) а(х) и Р(х) одного порядка малости; г) а(х) и Р(х) нельзя сравнивать.

1.15. Прих—>1 укажите ВСЕ верные утверждения:

Непрерывность

2.1. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото­ рых функция имеет в точкеаразрыв второго рода.

2.2. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото­ рых функция имеет в точкеаразрыв первого рода.

2.3. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото­ рых функция непрерывна в точкеа:

Верно?

а) с- точка неустранимого разрыва первого рода; б) с- точка устранимого разрыва первого рода; в) с -точка разрыва второго рода; г) с- точка непрерывности.

2.5. Известно, что Нт /(х)=— 5; lim / (х) = — 5 ; f[c) = — 5. Какое из ут-

Верждений верно?

а) с- точка неустранимого разрыва первого рода; б) с- точка устранимого разрыва первого рода; в) с -точка разрыва второго рода; г) с- точка непрерывности.

2.6. Укажите, в каком случае в точке с функция Дх) имеет устранимый разрыв:

Дифференциальное исчисление функции одной переменной

3.1. Какое из нижеперечисленных предложений определяет производ­ ную функции (когда приращение аргумента стремится к нулю)?

а) Отношение приращения функции к приращению аргумента; б) Предел отношения функции к приращению аргумента; в) Отношение функции к пределу аргумента; г) Отношение предела функции к аргументу;

д) Предел отношения приращения функции к приращению аргумента.

3.2. Первая производная функции показывает

а) скорость изменения функции; б) направление функции; в) приращение функции;

г) приращение аргумента функции.

3.3. Угловой коэффициент касательной, проведенной к графику функ­ ции в некоторой точке, равен

а) отношению значения функции к значению аргумента в этой точке; б) значению производной функции в этой точке; в) значению дифференциала функции в этой точке; г) значению функции в этой точке;

д) значению тангенса производной функции в этой точке.

3.4. На рисунке 3.1 изображен график функцииу= f ( x ) .Тогда произ­

водная/ х)это .

а) ТК/МК; б) NK/MK; b)N K ; г) МК/ТК; д) MN/MK; е) MN.

У

Рис. 3.1

3.5. На рисунке 3.2 изображен график функции у = fix’) . Найдите зна­

чение /7(1,5).

Рис. 3.2

3.6. Укажите функции, для которых существует конечная производная

в каждой точке числовой оси:

a)y = lruc; 6)y=|siruc|; в )у = х3; г)у = Зх ; д)у= [х.

3.7. Укажите ВСЕ верные утверждения: если функция дифференцируе­ ма в некоторой точке, то в этой точке .

а) функция не определена; б) можно провести касательную к графику функции;

в) нельзя провести касательную к графику функции; г) функция непрерывна; д) функция имеет экстремум.

3.8. Дифференциал функции равен

а) отношению приращения функции к приращению аргумента; б) произведению приращения функции на приращение аргумента; в) произведению производной на приращение аргумента;

г) приращению функции; д) приращению аргумента.

3.9. Дифференциал постоянной равен.

а) этой постоянной; б) произведению данной постоянной на величину Ах;

в) бесконечно большой величине; г) нулю; д) невозможно определить.

3.10. На рисунке 3.3 изображен график функции у = f ( x ) . Какой отре­ зок на этом рисунке соответствует дифференциалуdyl

У

Рис. 3.3

а) ТК; 6)NK; в) NT; г) МК; д) MN; е) другой ответ.

3.11. Какое из следующих утверждений верно для любой линейной функции?

а) дифференциал функции равен приращению функции; б) дифференциал функции равен приращению аргумента; в) дифференциал функции — это постоянная величина;

г) дифференциал функции равен производной этой функции.

3.12. Какое из следующих утверждений верно для нелинейной функ­

Ции?

а) дифференциал функции равен производной этой функции; б) дифференциал функции равен приращению аргумента; в) дифференциал функции равен части приращения функции; г) дифференциал функции — это постоянная величина.

3.13. Если функция у(х) непрерывна на[а;Ь],дифференцируема на (а;Ь)

и у<а) =у<Ь), то на(а;Ь)можно найти хотя бы одну точку,в которой

а) функция не определена; б) производная функции не существует;

в) нельзя провести касательную к графику функции; г) производная функции обращается в ноль.

Рис. 3.4

3.18. Какому условию удовлетворяет функция, график которой изобра­ жен на рисунке 3.5?

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Какое уравнение не имеет корней? Примеры уравнений

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Видео:4.Квадратное уравнение. Дискриминант отрицательный.Скачать

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

Видео:7. Неполное квадратное уравнение.Скачать

1. Линейное уравнение

Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

Видео:Решаем уравнения с корнем без ошибок.Уровень ЕГЭ.Скачать

3. Тригонометрические уравнения

Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Видео:Уравнения с корнями.Ошибки в решении.Скачать

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

«Решаем с помощью производной»

Разделы: Математика

Производная широко применяется при решении ряда задач элементарной математики. Из всего круга таких задач выделим те, при решении которых используется теорема Лагранжа и ее следствия. К ним относятся задачи на доказательство тождеств, неравенств, вывод формул тригонометрии, разложение алгебраических выражений на множители, решение уравнений, неравенств, систем уравнений, уравнений с параметрами. При этом можно указать общие методы решения и некоторые частные приемы.

Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что .

Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].

Следствие 2. Если функции и непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.

Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.

Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.

Теорему Лагранжа можно применять:

— при доказательстве неравенств, в частности – числовых неравенств;

— при исследовании вопроса о корнях многочлена или уравнения;

— при решении уравнений.

В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа , c (a;b) и оценивается f’(c), а, следовательно, и выражение , что позволяет доказать рассматриваемое неравенство или решить вопрос о корнях многочлена, уравнения.

Пример 1. Доказать, что .

Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), . Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и , где 0,6 , т.е. . Оценим число . Так как 0,6 2 . Тогда и окончательно .

Пример 2. Доказать, что e x >=ex.

Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=e x -ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b , т.е. . Так как c>1 при b>1, то e c >e и, следовательно, e c -e>0. Тогда , а значит e b -eb>0, т.е. e b >eb для любого b>1. Таким образом доказано, что e x >=ex при x>=1.

Если b , т.е. с c c -e , следует, что e b -eb>0, т.е. e b >eb.

Итак, доказано, что неравенство e x >=ex верно при любом действительном х. В частности, при x=c+1 получим e c+1 >=e(c+1), т.е. e c >=c+1, где с – любое действительное число.

Пример 3. Доказать, что уравнение не имеет действительных положительных корней.

Решение. Пусть b – любое положительное число. Рассмотрим функцию f(x)= , непрерывную на отрезке [a;b] и имеющую производную на интервале (0;b). По теореме Лагранжа имеем , 0 . А так как при любом с>0 e c >c+1 (доказано в примере 2), то e c -c>1 и, следовательно, . Отсюда получим , а значит для любого b>0. Таким образом, при x>0, т.е. , следовательно, равенство не выполняется ни при каком x>0. А, значит, уравнение не имеет действительных положительных корней.

Пример 4. Доказать, что на промежутке (0, 2) имеется не более двух различных действительных корней уравнения .

Решение. Предположим, что уравнение имеет не менее трех различных действительных корней х₁, х₂, х₃, принадлежащих промежутку (0,2), и пусть x₁ , т.е. f(x₁)=f(x₂)=f(x₃)=0. На каждом из отрезков [x₁;x₂], [x₂;x₃] для функции f(x) выполняются условия теоремы Лагранжа, следовательно, существуют числа c₁ и с₂ из интервалов (х₁;х₂), (х₂;х₃) соответственно, такие, что и . А так как f(x₁)=f(x₂)=f(x₃)=0, то f’(c₁)=0 и f’(c₂)=0, причем с₁с₂.

Найдем производную f’(x):

. Так как для любых х, то уравнение f’(x)=0 имеет единственный корень x=, принадлежащий промежутку (0, 2). Пришли к противоречию, так как с₁ и с₂ (с₁с₂) являются корнями уравнения f’(x)=0, тем самым доказано, что уравнение имеет на промежутке (0,2) не более двух различных действительных корней.

Пример 5. Решить уравнение x 9 -9x 5 +63x-55=0.

Решение. Легко заметить, что число х₁=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х₂, отличный от х₁. Числа х₁ и х₂ являются нулями функции f(x)=x 9 -9x 5 +63x-55 и, следовательно, f(x₁)=f(x₂)=0. Применим терему Лагранжа к функции f(x) на отрезке [x₁;x₂], если x₁ x₂. Следовательно, найдется такая внутренняя точка с этого отрезка, что будет выполняться . Учитывая, что f(x₁)=f(x₂)=0, получим f’(с)=0, т.е. число с – корень уравнения f’(x)=0. Но производная f’(x)=9x 8 -45x 4 +63, т.е. f’(x)=9(x 4 -2,5) 2 +6,75 положительна для любых х, а значит уравнение f’(x)=0 не имеет корней. Полученное противоречие доказывает, что найденный корень х₁=1 является единственным корнем уравнения x 9 -9x 5 +63x-55=0.

Определить число критических точек функции y=(x 2 -1)(x 2 -8х)(x-9).

Решение. Так как степень многочлена f(x)= (x 2 -1)(x 2 -8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней. Применим теорему Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках [-1;0], [0;1], [1;8], [8;9] и при этом учтем, что f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся внутренние точки х₁, х₂, х₃, х₄ соответственно, такие, что , , , , т.е. f’(x₁)=0, f’(x₂)=0, f’(x₃)=0, f’(x₄)=0. А учитывая, что x₁, х₂, х₃, х₄ – различные корни многочлена f’(x) четвертой степени, делаем вывод, что других корней, отличных от полученных, нет и, следовательно, функция y=(x 2 -1)(x 2 -8х)(x-9) имеет четыре критические точки.

Условие монотонности функции можно применять:

— при решении неравенств;

— при доказательстве неравенств с переменной;

— при доказательстве числовых неравенств;

— при исследовании вопроса о количестве корней уравнения;

— в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.

Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.

Пример 7. Доказать, что 3xcosx .

Решение. Докажем, что, если 0 , то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке функцию f(x)=tgx-3x+2sinx. Ее производная при принимает положительные значения, следовательно, функция f(x) возрастает на промежутке и на нем f(x)>f(0).

Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0. А так как на промежутке cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано, что sinx+sin2x-3xcosx>0, то есть, что 3xcosx .

Пример 8. Доказать, что

1) и , если 0 и , если e . Так как ее производная равна нулю при х=е, а при 0 0 и f’(x) e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+) — убывает. Тогда для любых значений х₁ и х₂ таких, что 0 . Запишем его в виде , . Учитывая, что функция ln t возрастающая, получим . А если обе части неравенства умножить на произведение x₁x₂>0, то получим x₂lnx₁ , откуда и будем иметь .

Если же e f(x₂), то есть , откуда и получим и .

Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.

Пример 9. Сравнить (сtg48°) tg48° и (сtg50°) tg50° .

Решение. Заметим, что сtg48°=сtg , tg48°=tg , ctg50°=ctg , tg50°=tg , а также, что . Взяв , и учитывая, что , если 0 , т.е. (сtg48°) tg48° > (сtg50°) tg50° .

Пример 10. Доказать, что 2006 2007 >2007 2006 .

Решение. Воспользуемся неравенством x₁ x2 >x₂ x1 , если e 2007 >2007 2006 .

Определить число действительных корней уравнения 2х 3 -24х-19=0.

Решение. Функция f(x)= 2х 3 -24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x 2 -24=6(x-2)(x+2).

При x 2 f’(x)>0, а при –2 0, f(2)=-51 0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х 3 -24х-19=0 имеет три действительных корня, которые находятся на промежутках (-3;-2), (-2;2), (2;5).

Остальные следствия теоремы Лагранжа можно применять:

— при доказательстве тождеств, в частности при выводе формул элементарной математики;

— при упрощении выражений;

— при разложении алгебраических выражений на множители.

При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.е. имеет вид f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x), и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту постоянную находят, положив х равным некоторому значению х₁.

Пример 12. Вывести формулу .

Решение. Функция f(x)= непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin 2 0-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим =0, или .

Пример 13. Доказать, что arctgx=arcsin при x , тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.

, . Так как при x и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin , то есть Итак, получим arctgx=arcsin при x

Решение. Заметим, что , для любого действительного х и функции , непрерывны на всей числовой прямой. Имеем ,

1) Рассмотрим функцию F(x)=f(x)+g(x), x (-;-1) (0;1).

F(x)= , а F’(x)=f’(x)+g’(x)= . Если x (-;-1), то |х 2 -1|=х 2 -1, |х|=-х и F’(x)=0. Если x (0;1), то |х 2 -1|=-(х 2 -1), |х|=х и F’(x)=0. На основании условия постоянства функции F(x)=c, то есть . На каждом из рассматриваемых промежутков определим с, положив, например, х= и x= .

, cледовательно, с=.

, следовательно, с=0. Имеем: при x (-;-1), при x (0;1).

2) Рассмотрим функцию G(x)=f(x)-g(x), x (-1;0) (1; +).

Если x (-1;0), то |х 2 -1|=-(х 2 -1), |x|=-x и G’(x)=0.

Если x (1; +), то |х 2 -1|=х 2 -1, |x|=x и G’(x)=0. Тогда на указанных промежутках функция G(x) постоянна, т.е. . Положим x= и x= , получим , следовательно, с=; , тогда с=0.

Имеем: при x (-1;0), при x (1;+ ).

3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.

f(-1)=arccos(-1)=, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=+g(x), то есть . , , следовательно, при х=0 f(x)=-g(x), то есть . f(1)=arccos1=0, g(1)=arcsin0=0, следовательно, при х= 1 f(x)=g(x), то есть .

Таким образом, данное тождество доказано для всех действительных х.

Пример 15. Разложить на множители выражение

y 2 (x-z)+x 2 (z-y)+z 2 (y-x).

Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y 2 (x-z)+x 2 (z-y)+z 2 (y-x).

f’(x)=y 2 +2x(z-y)-z 2 =y 2 -z 2 -2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).

Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.

g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x 2 ).

Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)((y+z)x-x 2 )+c. Найдем с, полагая в этом равенстве, например, х=0. Имеем yz 2 -zy 2 =c. Тогда f(x)=g(x)+yz 2 -zy 2 , то есть

f(x)=(y-z)((y+z)x-x 2 )+yz 2 -zy 2 =(y-z)(xy+xz-x 2 )-yz(y-z)=(y-z)(xy-x 2 +xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).

Итак, y 2 (x-z)+x 2 (z-y)+z 2 (y-x)=(y-z)(y-x)(x-z).

💥 Видео

#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Откуда три корня? ➜ Решите уравнение z³=1Скачать

Найди действительные корни.Повторение.9 класс.Скачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Как правильно решать уравнения с корнями.Иррациональные уравнения.Скачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

ЗАДАНИЕ 5|ЕГЭ ПРОФИЛЬ МАТЕМАТИКА| Решите уравнение x=-x-10/x+6. Если уравнение имеет более одногоСкачать

Найдите корень уравнения: корень из (11-5x)=1-x. Если уравнение имеет более одного корня... (ЕГЭ)Скачать

7 класс. Учебник Макарычев. N526a. Докажите, что не имеет корней уравнение. а)х^2+1=0Скачать

Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать