
Сейчас речь пойдет о трех страшных буквах: l o g.
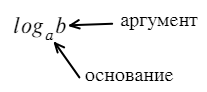
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c» . Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182. мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета. Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.
А теперь посложнее, перейдем по определнию к показательному уравнению :
Следующий пример поможет нам узнать первую формулу логарифмов:
Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?
Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.
Нетрудно тогда понять, что есть еще одно следствие:
В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!
Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.
Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.
Основное логарифмическое тождество:
В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.
Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.
Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает:
А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:
Дальше с этим ничего сделать не сможем.
Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.
Видим сложение логарифмов, выпускаем эту формулы:
А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:
Видим разность логарифмов, выпускаем эту формулы:
А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:
Теперь посмотрим на степени у аргмента логарифма:
А в основании тоже можно? Нужно!
Минус два — это степень у основания:
А все вместе можно? Конечно, логарифмы — это такая свобода:
А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов
С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.
Формула перехода к новому основанию:
Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.
Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.
Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.
Последняя формула, меняем местами аргумент и основание логарифма:
Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.
Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:
Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.
Начинаем с внутреннего:
И постепенно раскрываем каждый последующий:
После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.
Все логарифмические уравнения решаем по одному из двух алгоритмов.
Первый появляется из определения логарифма:
Только не забываем про ОДЗ:
Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием:
Не забываем про ОДЗ, тогда получится:
Подставив в ОДЗ x = 15, видим, что все выполняется!
Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:
Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:
Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:
Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:
Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:
- Л О Г — это не три страшные буквы, а обратное действие возведению в степень.
- Хоть формул и целых девять, но они никак не пересекаются. Решая пример и ориентируясь в формулах, ты будешь однозначно выбирать необходимую формулу.
- Видишь логарифм — ищи ОДЗ и решай его в первую очередь!
- Решение уравнений происходит по одному из двух вариантов и больше никак.
- В неравенствах главное — помнить об основании логарифма, когда зачеркиваем логарифмы.
- Преобразование выражений с использованием свойств логарифмов: примеры, решения
- Свойства логарифмов
- Как преобразовать числовое выражение с логарифмом
- Как выбрать свойство логарифма для преобразования
- Задачи с применением нескольких свойств логарифмов
- Предварительное преобразование перед применением основных свойств логарифмов
- Как выделить степень в основании логарифма и под его знаком
- Как применять свойства степени при преобразовании выражений с логарифмами
- Преобразование логарифмов с десятичными дробями
- Преобразование выражений с отрицательными числами под знаком логарифма
- Как преобразовать логарифмическое выражение с переменными
- Особенности преобразований выражений с переменными
- Почему надо учитывать область допустимых значений
- Правила проведения преобразований
- Как решать логарифмические уравнения подробный разбор примеров
- Сложение и вычитание логарифмов.
- Что такое логарифм и как его посчитать
- Два очевидных следствия определения логарифма
- Свойства логарифмов
- Степень можно выносить за знак логарифма
- Логарифм произведения и логарифм частного
- Формула перехода к новому основанию
- Сумма логарифмов. Разница логарифмов
- Логарифмический ноль и логарифмическая единица
- Как решать уравнения с логарифмами: 2 способа с примерами
- Сравнение логарифмов
- Пример Найдите корень уравнения.
- Логарифмы со специальным обозначением
- Десятичный логарифм
- Натуральный логарифм
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: a log a b = b , a > 0 , a ≠ 1 , b > 0 . Также нужно помнить следующие свойства:
- log a 1 = 0 при любом a > 0 , a ≠ 1 .
- log a a = 1 , если a > 0 , a ≠ 1 .
- logaa=1 log a a = 1 при любом a > 0 , a ≠ 1 .
- log a a = 1 , если a > 0 , a ≠ 1 .
- log a a p = p , при этом a > 0 , a ≠ 1 и p может быть любым действительным числом.
- log a ( x · y ) = log a x + log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . В обобщенном виде это свойство можно представить как log a ( x 1 · x 2 · … · x n ) = log a x 1 + log a x 2 + … + log a x n , a > 0 , a ≠ 1 , x 1 > 0 , x 2 > 0 , … , x n > 0
- ) log a x y = log a x — log a y .
- log a x y = log a x — log a y , при этом a > 0 , a ≠ 1 , x > 0 , y > 0 .
- log a x y = log a x — log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 .
- log a b p = p · log a b , при этом a > 0 , a ≠ 1 , b > 0 , а p может быть любым действительным числом.
- это свойство является следствием предыдущего: log a b n = 1 n · log a b , a > 0 , a ≠ 1 , n может быть любым натуральным числом больше 1 , b > 0 .
- log a b = log c b log c a , при этом a > 0 , a ≠ 1 , b > 0 , c > 0 , c ≠ 1 .
- свойство, также являющееся следствием: log a b = 1 log b a , где a > 0 , a ≠ 1 , b > 0 , b ≠ 1 .
- log a q b p = p q · log a b , a > 0 , a ≠ 1 , b > 0 , p и q могут быть любыми действительными числами, q ≠ 0
- log a q b p = p q , a > 0 , a ≠ 1 , p и q – любые действительные числа, q ≠ 0 .
- log a q a p = p q , b log a c = c log a b , при этом a > 0 , a ≠ 1 , b > 0 , c > 0 .
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что b n = b 1 n , если b ≥ 0 . Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия log a q b p = p q · log a b и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
log a q b p = log a b p log a a q = p · log a b q = p q · log a b
То же относится и к последнему свойству из списка, выраженному формулой b log a c = C log a c = c log a b : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Видео:Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать

Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Видео:Логарифмические уравнения 🥷🏿Скачать

Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой a log a b = b , a > 0 , a ≠ 1 , b > 0 .
Условие: преобразуйте и вычислите значение следующих выражений: 1 ) 5 log 5 4 ; 2 ) 10 lg ( 1 + 2 · π ) , 3 ) 2 + 3 log 2 + 3 ln 15 ; 4 ) 2 log 2 ( − 7 ) ; 5 ) ( — 5 ) log — 5 e 3
Решение
В первом примере прослеживается формула a log a b . У нас есть a = 5 , b = 4 , что соответствует необходимому условию a > 0 , a ≠ 1 , b > 0 . Используем нужное равенство a log a b = b и получим 5 log 5 4 = 4 .
Во втором случае a будет равно 10 , b – 1 + 2 · π . Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10 l g ( 1 + 2 · π ) = 1 + 2 · π .
В третьем выражении у нас есть степень вида a log a b , причем a = 2 + 3 и b = ln 15 . Запишем: 2 + 3 log 2 + 3 ln 15 = ln 15 . Хотя равенство также соответствует формуле a log a b , где a равно 2 , а b = — 7 , мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, — 7 не соответствует условию b > 0 , что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2 log 2 ( − 7 ) = − 7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что — 5 log — 5 · e 3 = e 3 , поскольку такое выражение смысла не имеет.
Ответ: 1 ) 5 log 5 4 = 4 ; 2 ) 10 l g ( 1 + 2 · π ) = 1 + 2 · π ; 3 ) 2 + 3 log 2 + 3 ln 15 = ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1 , имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма a log a b = b , a > 0 , a ≠ 1 , b > 0 , но в перевернутом виде, т.е. прочитанное справа налево, например, 3 = e ln 3 или 5 = 5 log 5 5 .
Далее возьмем примеры с другими свойствами логарифмов.
Условие: вычислите, если возможно: 1 ) log − 2 1 , 2 ) log 1 1 , 3 ) log 0 1 , 4 ) log 7 1 , 5 ) ln 1 , 6 ) l g 1 , 7 ) log 3 , 75 1 , 8 ) log 5 · π 71 .
Решение
В первых трех примерах мы видим не имеющие смысла выражения log − 2 1 , log 1 1 , log 0 1 . Основанием логарифма не может быть число меньше 1 , в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7 , e , 10 , 3 , 75 и 5 · π 7 , а под знаками логарифма везде 1 . Зная соответствующее свойство логарифма ( log a 1 = 0 при любом a > 0 , a ≠ 1 ., мы можем сделать вывод, что значения этих выражений равны 0 .
Ответ: 1 , 2 , 3 смысла не имеют; 4 ) log 7 1 = 0 , 5 ) ln 1 = 0 , 6 ) l g 1 = 0 , 7 ) log 3 , 75 1 = 0 , 8 ) log 5 · e 7 1 = 0 .
Условие: вычислите значения: 1 ) log 1 3 1 3 , 2 ) ln e , 3 ) l g 10 , 4 ) log 5 · π 3 − 2 ( 5 · π 3 − 2 ) , 5 ) log − 3 ( − 3 ) , 6 ) log 1 1 .
Решение
Нам потребуется свойство логарифма, выраженное формулой log a a = 1 при a > 0 , a ≠ 1 . Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1 , 2 , 3 , 4 действительно ответом будет 1 , а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1 ) log 1 3 = 1 3 = 1 , 2 ) ln e = 1 , 3 ) l g 10 = 1 , 4 ) log 5 · π 3 − 2 ( 5 · π 3 − 2 ) = 1 ; 5 , 6 не имеют смысла.
Условие: вычислите: 1 ) log 3 3 11 , 2 ) log 1 + 2 2 ( 1 + 2 2 ) 7 2 3 , 3 ) log π 5 ( π 5 ) — 2 , 4 ) log − 10 ( − 10 ) 6 .
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство log a a p = p , где a > 0 , a ≠ 1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log 3 3 11 = 11
- log 1 + 2 2 ( 1 + 2 · 2 ) 7 2 3 = 7 2 3
- log π 5 ( π 5 ) — 2 = — 2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log − 10 ( − 10 ) 6 = 6 не имеет смысла.
Ответ: 1 ) log 3 3 11 = 11 , 2 ) log 1 + 2 2 ( 1 + 2 · 2 ) 7 2 3 = 7 2 3 , 3 ) log π 5 ( π 5 ) — 2 = — 2 , 4 ) не имеет смысла.
Условие: даны выражения log 2 , 6 4 · 1 2 7 , ln 2 + 1 π и l g ( ( − 5 ) · ( − 12 ) ) . Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: log a ( x · y ) = log a x + log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log 2 , 6 4 · 1 2 7 = log 2 , 6 4 + log 2 , 6 1 2 7
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: log a x y = log a x — log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . Здесь в основании стоит положительное число e , также у нас есть положительный числитель 2 + 1 и знаменатель π , т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln 2 + 1 π = ln 2 + 1 — ln π .
Разберем третий пример. Начнем с того, что выражение l g ( ( − 5 ) · ( − 12 ) ) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа — 5 и — 12 отрицательны. Значит, преобразование l g ( ( − 5 ) · ( − 12 ) ) = l g ( − 5 ) + l g ( − 12 ) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: l g ( ( − 5 ) · ( − 12 ) ) = l g ( 5 · 12 ) = l g 5 + l g 12 .
Ответ: 1 ) log 2 , 6 4 · 1 2 7 = log 2 , 6 4 + log 2 , 6 1 2 7 , 2 ) ln 2 + 1 π = ln 2 + 1 — ln π , 3 ) l g ( ( − 5 ) · ( − 12 ) ) = l g 5 + l g 12 .
Условие: упростите выражения log 3 0 , 25 + log 3 16 + log 3 0 , 5 и ln 2 3 — ln 1 3 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log 30 , 25 + log 3 16 + log 3 0 , 5 = log 3 ( 0 , 25 · 16 · 0 , 5 ) = log 3 2 , а во втором ln 2 3 — ln 1 3 = ln 2 3 : 1 3 = ln 2 .
Ответ: 1 ) log 30 , 25 + log 3 16 + log 3 0 , 5 = log 3 ( 0 , 25 · 16 · 0 , 5 ) = log 3 2 , 2 ) ln 2 3 — ln 1 3 = ln 2 .
Условие: есть выражения log 0 , 7 5 11 , log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 и log 3 ( − 5 ) 6 . Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида log a b p . Берем свойство, которое выражается формулой вида
log a b p = p · log a b , где a > 0 , a ≠ 1 , b > 0 , p — любое действительное число. Поскольку условия a > 0 , a ≠ 1 , b > 0 выполнены, то мы можем преобразовать log a b p в произведение p · log a b .
- в случае с первым выражением a равно 7 , b – пяти и p – 11 . Тогда log 0 , 7 5 11 = 11 · log 0 , 7 5 .
- тут a = 3 — 1 , b = 3 — 2 + 5 · 67 3 , p = 5 + 1 . Нужные условия выполнены, значит, мы можем записать, что:
log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 = = 5 + 1 · log 3 — 1 ( 3 — 2 + 5 · 67 3 ) - у нас есть выражение той же структуры: log a b p , a = 3 , b = − 5 , p = 6 , однако одно из условий не выполняется, а именно b у нас меньше 0 . Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log 3 ( − 5 ) 6 = log 3 5 6 = 6 · log 3 5 .
Ответ: 1 ) log 0 , 7 5 11 = 11 · log 0 , 7 5 , 2 ) log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 = = 5 + 1 · log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 3 ) log 3 ( − 5 ) 6 = 6 · log 3 5 .
Применение формулы в обратном порядке в виде p · log a b = log a b p требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3 · ln 5 = ln 5 3 и l g 2 · log 2 3 = log 2 3 l g 2 .
Условие: согласно таблице логарифмов, l g 2 ≈ 0 , 3010 и l g 5 ≈ 0 , 6990 . Вычислите, сколько будет log 2 5 . Здесь же: запишите ln 11 ln 3 в виде логарифма, основание которого равно 3 .
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log 2 5 = l g 5 l g 2
Вычисляем и находим ответ: l g 5 l g 2 ≈ 0 , 6990 0 , 3010 ≈ 2 , 3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. log c b log c a = log a b .
Считаем: ln 11 ln 3 = log 3 11
Ответ: 1 ) log 2 5 ≈ 2 , 3223 , 2 ) ln 11 ln 3 = log 3 11 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Условие: 1 ) дан логарифм ln 1 + π 7 . Необходимо избавиться от корня под знаком логарифма; 2 ) выполните преобразование дроби 1 log 2 5 в логарифм с основанием 4 ; 3 ) преобразуйте логарифм log e 2 3 4 5 так, чтобы избавиться от степени в основании; 4 ) вычислите, сколько будет log 2 — 1 3 2 1 6 ; 5 ) осуществите замену 2 , 3 log 7 3 на степень с основанием 3 .
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой log a b n = 1 n · log a b .В первом случае можем сразу же подсчитать: ln 1 + π 7 = 1 7 · ln ( 1 + π ) .
- во втором случае нам понадобится формула log a b = 1 log b a , примененная в обратном порядке. Получим 1 log 2 5 = log 5 2 .
- здесь нам потребуется свойство log a q b p = p q · log a b . Применяем его и получаем log e 2 3 4 5 = 4 5 2 · ln 3 = 2 5 · ln 3 .
- в этом случае нам нужно будет следствие, выраженное формулой log a q a p = p q : log ( 2 ) — 1 3 2 1 6 = 1 6 — 1 3 = — 1 2
- используем формулу свойства b log a c = c log a b и вычисляем ответ:
2 , 3 log 7 · 3 = 3 log 7 2 , 3
Ответ: 1 ) ln 1 + π 7 = 1 7 · ln ( 1 + π ) ; 2 ) 1 log 2 5 = log 5 2 ; 3 ) log e 2 3 4 5 = 2 5 · ln 3 ; 4 ) log ( 2 ) — 1 3 2 1 6 = — 1 2 . 5 ) 2 , 3 log 7 · 3 = 3 log 7 2 , 3 .
Видео:Логарифмическое уравнение / Как решить?Скачать

Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Условие: вычислите, сколько будет ( log 3 15 − log 3 5 ) · 7 log 7 5 .
Решение
Мы можем заменить выражение в скобках логарифмом log 3 ( 15 : 5 ) , используя свойство частного. Вычисляем его значение и получаем log 3 ( 15 : 5 ) = log 3 3 = 1 .
Согласно основному определению логарифма, значением 7 log 7 5 будет 5 . Подставим в исходное выражение получившиеся результаты и найдем, что ( log 3 15 − log 3 5 ) · 7 log 7 5 = 1 · 5 = 5 .
Вот все решение без комментариев:
( log 3 15 − log 3 5 ) · 7 log 7 5 = log 3 ( 15 : 5 ) · 5 = = log 3 3 · 5 = 1 · 5 = 5
Ответ: ( log 3 15 − log 3 5 ) · 7 log 7 5 = 5 .
Условие: вычислите, чему равен log 3 log 2 2 3 − 1 .
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log 2 2 3 = 3 . Получим, что log 3 log 2 2 3 = log 3 3 , а дальше log 3 3 = 1 . Следовательно, log 3 log 2 2 3 − 1 = 1 − 1 = 0 .
Ответ: log 3 log 2 2 3 − 1 = 0 .
Условие: выполните упрощение выражения 3 ln 5 ln 3 log 5 2 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5 ln 3 как log 3 5 . У нас получилось 3 log 3 5 log 5 2 . Теперь применяем формулу основного определения логарифма 3 log 3 5 = 5 и получаем, что 3 log 3 5 log 5 2 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2 .
Ответ: 3 ln 5 ln 3 log 5 2 = 2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log 3 3 4 , 5 2 + log 5 3 , lg 0 , 01 . Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 5 2 + log 5 3 = 5 2 · 5 log 5 3 = 25 · 3 = 75 , log 3 3 4 = log 3 1 2 3 4 = 4 1 2 = 8 и l g 0 , 01 = l g 10 − 2 = − 2 . Разберем подробнее, как именно это делается.
Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln 2 5 3 2 3 32 , log 3 81 .
- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2 log 2 2 3 , 3 2 · log 35 , 7 1 + log 74 , 25 ( log 3 5 ) — 3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log 1 5 ( 0 , 2 ) 7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде l g ( − 3 ) − 4 , log 6 ( ( − 9 ) · ( − 4 ) ) и др.
Разберем подробно каждый вид преобразования.
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log 1 9 81 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 1 9 . Их легко представить в виде степени с основанием 3 : 81 = 3 4 и 1 9 = 3 − 2 . Значит, все выражение можно переписать как log 3 — 2 3 4 , а здесь уже видна возможность использования свойства log a q b p = p q · log a b . Таким образом, log 1 9 81 = log 3 — 2 = 4 — 2 = — 2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3 , которые легко узнать с первого взгляда: 243 = 3 5 , 81 = 3 4 , 8 = 2 3 , 64 = 2 6 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10 , чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10 , 100 и др.
Условие: вычислите или упростите выражения log 6 216 , log 343 1 243 , log 0 , 000001 0 , 001 .
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 6 3 . Значит, log 6 216 = log 6 6 3 = 3 .
- у нас есть числа 343 и 1 243 . Обратимся к таблице степеней и увидим, что их можно представить в виде 7 3 и 3 − 4 . Выполняем дальнейшие преобразования и получаем:
log 343 1 243 = log 7 3 3 — 4 = = — 4 3 · log 7 3 = — 1 1 3 · log 7 3 - Поскольку 0 , 000001 = 10 − 6 и 0 , 001 = 10 − 3 , тогда log 0 , 000001 0 , 001 = log 10 − 6 10 − 3 = — 3 — 6 = 1 2
Ответ: 1 ) log 6 216 = 3 , 2 ) log 343 1 243 = — 1 1 3 · log 7 3 ; 3 ) log 0 , 000001 0 , 001 = 1 2 .
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Условие: упростите выражение log 3 648 · log 2 3 .
Решение
Выполняем разложение 648 на простые множители.
648 324 162 81 9 3 1 2 2 2 3 3 3
Значит, это число можно представить в виде 648 = 2 3 · 3 4 . Следовательно, log 3 648 · log 2 3 = log 3 ( 2 3 · 3 4 ) · log 2 3
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log 3 ( 2 3 · 3 4 ) · log 2 3 = ( log 3 2 3 + log 3 3 4 ) · log 2 3 = = ( 3 · log 3 2 + 4 ) · log 2 3 .
Упрощаем выражение через раскрытие скобок:
( 3 · log 3 2 + 4 ) · log 2 3 = 3 · log 3 2 · log 2 3 + 4 · log 2 3 .
В полученном выражении log 3 2 · log 2 3 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3 · log 3 2 · log 2 3 + 4 · log 2 3 = 3 · 1 + 4 · log 2 3 = 3 + 4 · log 2 3 .
Ответ: log 3 648 · log 2 3 = 3 + 4 · log 2 3 .
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 3 2 3 · 3 — 2 , 2 · 2 2 7 3 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Условие: найдите значение выражений log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 и log 3 729 1 9 .
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 5 2 · 5 − 0 , 5 · 5 − 1 = 5 2 − 0 , 5 − 1 = 5 0 , 5 . Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
5 3 4 5 4 = 5 3 4 4 = 5 3 4 — 4 = 5 — 3 1 4
Полученное выражение подставим в исходный логарифм, применив формулу log a q a q = p q , и получим ответ:
log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 = log 5 0 . 5 5 — 3 1 4 = — 3 1 4 0 . 5 = = — 13 4 1 2 = — 13 2 = — 6 1 2
Во втором случае представим число 729 как 3 6 , а 1 9 как 3 − 2 . Исходный логарифм приобретет вид log 3 3 6 3 — 2 . Используя свойство корня из степени, преобразуем основание логарифма и получим:
3 3 6 = 3 3 3 = 3 1 — 3 = 3 — 2
Заканчиваем преобразование: log 3 3 6 3 — 2 = log 3 — 2 3 — 2 = 1 .
Ответ: 1 ) log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 = — 6 1 2 ; 2 ) log 3 729 1 9 = 1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Условие: вычислите значения log 1 3 — 1 1 32 · 3 + 1 — 5 и log 2 · cos 1 ( 1 + cos 2 ) 3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
1 3 — 1 = 3 + 1 3 — 1 · 3 + 1 = 3 + 1 3 2 — 1 2 = 3 + 1 2
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
1 32 · 3 + 1 — 5 = 3 + 1 5 32 = 3 + 1 5 2 5 = 3 + 1 2 5
В результате преобразований у нас получился логарифм степени основания log 3 + 1 2 3 + 1 3 5 . Значение данного выражения будет равно 5 .
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos 2 a = 1 + cos 2 a 2 :
log 2 · cos 1 ( 1 + cos 2 ) 3 = log 2 · cos 1 ( 2 · cos 2 1 ) 3
Преобразуем второй логарифм, записав его как степень 2 · cos 2 1 1 2 или же 2 · cos 1 2 3 = 2 · cos 1 6 . Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1 ) log 1 3 — 1 1 32 · 3 + 1 — 5 = 5 ; 2 ) log 2 · cos 1 ( 1 + cos 2 ) 3 = 6 .
Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать

Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями a p · a q = a p + q . Чаще всего его применяют в обратном порядке, т.е. справа налево.
Условие: вычислите значения 3 − 2 + log 3 7 и 0 , 7 2 − log 0 , 7 0 , 1 .
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3 − 2 + log 3 7 = 3 − 2 · 3 log 3 7 . Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3 − 2 · 3 log 3 7 = ( 1 9 ) · 7 = 7 9
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0 , 7 2 − log 0 , 7 0 , 1 = 0 , 7 2 · 0 , 7 − log 0 , 7 0 , 1 . После этого нам нужно представить показатель − log 0 , 7 0 , 1 в виде l log 0 , 7 ( 0 , 1 ) − 1 = log 0 , 7 10 . Теперь все, что нам осталось, – это закончить вычисления:
0 , 7 2 · 0 , 7 − log 0 , 7 0 , 1 = 0 , 49 · 0 , 7 log 0 , 7 10 = 0 , 49 · 10 = 4 , 9
Ответ: 1 ) 3 − 2 + log 3 7 = 7 9 ; 2 ) 0 , 7 2 − log 0 , 7 0 , 1 = 4 , 9 .
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой ( a p ) q = a p · q , например, если у нас есть выражение ( e ln 2 ) 3 , то мы можем заключить, что значение части в скобках будет равно 2 . Значит, ( e ln 2 ) 3 = 2 3 = 8 . А если в условии указано ( e 3 ) ln 2 или ( e 3 ) ln 2 , то мы сначала приводим их к виду ( e ln 2 ) 3 :
e 3 · ln 2 = e ln 2 · 3 = ( e ln 2 ) 3 и ( e 3 ) ln 2 = e 3 · ln 2 = e ln 2 · 3 = ( e ln 2 ) 3 .
Посмотрим пример решения такой задачи.
Условие: выполните упрощение выражений 2 log 2 2 3 − 3 log 2 3 и 5 ( log 8 5 ) − 1 .
Решение
Отметим, что выражения 2 log 2 2 3 и 2 log 2 2 3 не являются равными друг другу. Мы можем представить 2 log 2 2 3 как 2 log 2 3 · log 2 3 . Используя свойство степени, представим его как ( 2 log 2 3 ) log 2 3 , что будет тождественно равным 3 log 2 3 . В итоге мы имеем, что 2 log 2 2 3 − 3 log 2 3 = 3 log 2 3 − 3 log 2 3 = 0 .
Вот запись всего решения:
2 log 2 2 3 − 3 log 2 3 = 2 log 2 3 · log 2 3 − 3 log 2 3 = = ( 2 log 2 3 ) log 2 3 − 3 log 2 3 = 3 log 2 3 − 3 log 2 3 = 0
Перейдем ко второму примеру. Запись 25 ( log 8 5 ) — 1 не будет равна ( 25 log 8 5 ) − 1 . Мы можем представить степень ( log 8 5 ) − 1 как дробь 1 log 8 5 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле log a b = 1 log b a , чтобы получить log 5 8 .
Так, 25 ( log 8 5 ) — 1 = 25 log 5 8 . Поскольку 25 – это 5 2 , имеем 5 log 5 8 = ( 5 2 ) log 5 8 . То, что у нас получилось, представляем в виде ( 5 log 5 8 ) . Нам осталось только вычислить значение: ( 5 log 5 8 ) 2 = 8 2 = 64 .
Ответ: 1 ) 2 log 2 2 3 − 3 log 2 3 = 0 , 2 ) 25 ( log 8 5 ) − 1 = 64 .
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
4 − 0 , 5 + 2 · log 4 3 = 4 − 0 , 5 · 4 2 · log 4 3 = = 1 2 · ( 4 log 4 3 ) 2 = 1 2 · 3 2 = 1 2 · 9 = 4 , 5
Видео:84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log 0 , 4 2 5 3 ? Отметим, что 2 5 и 0 , 4 равны между собой 0 , 4 = 4 10 = 2 5 , то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Условие: вычислите значение выражения log 0 , 4 6 , 25 .
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log 0 , 4 6 , 25 = log 4 10 625 100 = log 2 5 25 4
Теперь видно, что мы можем преобразовать 25 4 в виде ( 2 5 ) − 2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log 2 5 25 4 = log 2 5 2 5 — 2 = — 2
Ответ: — 2 .
Видео:Логарифмические уравнения. 11 класс.Скачать

Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log 3 — 9 3 — 27 или log 3 ( ( − 2 ) · ( − 5 ) ) .
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log 3 ( ( − 2 ) · ( − 5 ) ) к log 3 ( − 2 ) + log 3 ( − 5 ) , применить свойство логарифма степени к log 2 ( − 2 ) 6 или логарифма частного к log 3 — 9 3 — 27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log 3 ( ( − 2 ) · ( − 5 ) ) . Структура выражения соответствует формуле log a ( x · y ) , где a равно 3 , x — 3 и y — 5 . Поскольку условия a > 0 , a ≠ 1 , x > 0 , y > 0 не выполнены, формулу log a ( x · y ) = log a x + log a y мы применить не можем, и равенство log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 ( − 2 ) + log 3 ( − 5 ) записать нельзя. Преобразования вида log 3 — 9 3 — 27 = log 3 — 9 3 — log 3 ( — 27 ) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0 .
Вернемся опять к нашему примеру. Согласно правилам умножения, ( − 2 ) · ( − 5 ) = 2 · 5 , значит, log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 ( 2 · 5 ) . К выражению в таком виде мы уже можем применить формулу log 3 ( 2 · 5 ) = log 3 2 + log 3 5 . А вот для примера log 2 ( − 2 ) 6 нужно будет выполнить следующие действия:
( − 2 ) 6 = ( ( − 1 ) · 2 ) 6 = ( − 1 ) 6 · 2 6 = 1 · 2 6 = 2 6
Значит, log 2 ( − 2 ) 6 = log 2 2 6 = 6 .
Условие: найдите значение выражения log 2 — 16 3 — 2 — 2 3 .
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от — 16 3 — 2 — 2 3 к — 16 3 — 2 — 2 3 . Согласно правилам деления, получим — 16 3 — 2 — 2 3 = 16 3 2 — 2 3 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
16 3 2 — 2 3 = 2 4 3 2 — 2 3 = 2 4 3 2 — 2 3 = 2 4 3 — — 2 3 = 2 2 log 2 — 16 3 — 2 — 2 3 = log 2 2 2 = 2
Ответ: log 2 — 16 3 — 2 — 2 3 = 2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как log a ( x · y ) = log a | x | + log a | y | , где a > 0 , a ≠ 1 , x ≠ 0 , y ≠ 0 , то после преобразования мы получим log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 | − 2 | + log 3 | − 5 | = log 3 2 + log 3 5 .
Видео:Логарифмы в ЕГЭ⚡️что получилось?!Скачать

Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Видео:Интересная задача на логарифмы в ЕГЭСкачать

Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log 2 ( x + 1 ) 4 . При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством ( x + 1 ) 4 > 0 , значение которого является числовым множеством ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле log A B p , где A равно 2 , B – x + 1 , а p – четырем.
Мы видим, что заданное выражение соответствует виду log A B p , где A = 2 , B = x + 1 и p = 4 . Такие выражения преобразовываются по свойству логарифма степени log a b p = p · log a b . Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x = − 2 . В итоге: log 2 ( − 2 + 1 ) 4 = log 2 1 = 0 , а 4 · log 2 ( − 2 + 1 ) = 4 · log 2 ( − 1 ) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу log a b p = p · log a b , но это допустимо лишь при условии a > 0 , a ≠ 1 , b > 0 , p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x + 1 > 0 , что аналогично x > − 1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x > − 1 , но и из промежутка x − 1 . Но для x − 1 мы не имели права осуществлять преобразование по выбранной формуле.
Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Почему надо учитывать область допустимых значений
Продолжая работу с выражением log 2 ( x + 1 ) 4 , проанализируем, как изменится область значений, когда мы выполним переход к виду 4 · log 2 ( x + 1 ) . Ранее мы уже определили эту область как множество ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Теперь вычислим, какова будет область допустимых значений для 4 · log 2 ( x + 1 ) . Она определяется условием x + 1 > 0 , а ему, в свою очередь, будет отвечать множество ( − 1 , + ∞ ) . Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
- когда мы переходим от логарифма произведения к сумме, например, ln ( x · ( x + 3 ) ) = ln x + ln ( x + 3 ) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log 2 x sin x на log 2 x − log 2 sin x .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени log a b p = p · log a b и формулу log a b p = p q · log a b . Примеры таких преобразований – log x 3 ( x — 8 ) 2 = 2 3 · log x ( x — 8 ) , ln ( x + 3 ) − 4 = − 4 · ln ( x + 3 ) .
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4 · log 2 ( x + 1 ) к log 2 ( x + 1 ) 4 . В этом случае область расширяется от ( − 1 , + ∞ ) до ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4 · log 2 ( x + 1 ) = log 2 ( x + 1 ) 4 имеет место на области значений переменной x для исходного выражения 4 · log 2 ( x + 1 ) , то есть, при x + 1 > 0 , что аналогично ( − 1 , + ∞ ) .
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Видео:ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ: ОДЗ ИЛИ НЕ ОДЗ?Скачать

Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Условие: упростите 3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 .
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от l g ( x + 2 ) 7 к 7 · l g ( x + 2 ) и от l g ( x + 2 ) 4 к 4 · l g ( x + 2 ) , нам нужно, чтобы x + 2 > 0 . Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств ( x + 2 ) 7 > 0 , x + 2 > 0 , ( x + 2 ) 4 > 0 , которая будет равносильной условию x + 2 > 0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 = = 3 · 7 · l g ( x + 2 ) − l g ( x + 2 ) − 5 · 4 · l g ( x + 2 ) = = 21 · l g ( x + 2 ) − l g ( x + 2 ) − 20 · l g ( x + 2 ) = = ( 21 − 1 − 20 ) · l g ( x + 2 ) = 0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3 · l g ( x + 2 ) 7 — l g ( x + 2 ) — 5 · l g ( x + 2 ) 4 = = l g ( ( x + 2 ) 7 ) 3 — l g ( x + 2 ) — l g ( ( x + 2 ) 4 ) 5 = = l g ( x + 2 ) 21 — l g ( x + 2 ) — l g ( x + 2 ) 20 = = l g ( x + 2 ) 21 ( x + 2 ) · ( x + 2 ) 20 = l g 1 = 0
Ответ: 3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 = 0 .
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Условие: выполнить упрощение выражения l g ( x + 2 ) 4 − l g ( x + 2 ) 2 .
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x > − 2 и x − 2 . Если x > − 2 , то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: l g ( x + 2 ) 4 − l g ( x + 2 ) 2 = 4 · l g ( x + 2 ) − 2 · l g ( x + 2 ) = 2 · l g ( x + 2 ) . Однако в области значений есть и промежуток x + 2 0 , и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x + 2 при x + 2 0 как − | x + 2 | . В таком случае мы можем выполнить переход от l g ( x + 2 ) 4 − l g ( x + 2 ) 2 к l g ( − | x + 2 | ) 4 − l g ( − | x + 2 | ) 2 , и далее к l g | x + 2 | 4 − l g | x + 2 | 2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь | x + 2 | > 0 при любом x .
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при | x + 2 | 0 , имеем 2 · l g | x + 2 | = 2 · l g ( − ( x + 2 ) ) . Это и будет ответом на поставленный вопрос.
Ответ: l g ( x + 2 ) 4 — l g ( x + 2 ) 2 = 2 · l g ( x + 2 ) , x + 2 > 0 2 · l g ( — ( x + 2 ) ) , x + 2 0 . Можно записать ответ компактнее, используя знаки модуля: l g ( x + 2 ) 4 — l g ( x + 2 ) 2 = 2 · l g x + 2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Условие: представьте выражение ln x — 1 · x — 2 x — 3 как сумму и разность логарифмов линейных двучленов x − 1 , x − 2 и x − 3 .
Решение
Вычисляем область допустимых значений данного выражения:
x — 1 · x — 2 x — 2 > 0 , ( 1 , 2 ) ∪ 3 , + ∞
Поскольку значения x − 1 , x − 2 и x − 3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
ln x — 1 · x — 2 x — 3 = = ln ( x — 1 ) + ln ( x — 2 ) — ln ( x — 3 )
А на интервале от одного до двух значение x − 1 будет положительным, а x − 2 и x − 3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
ln x — 1 · x — 2 x — 3 = ln x — 1 · — x — 2 — x — 3 = = ln ( x — 1 ) · x — 2 x — 3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x − 1 , | x − 2 | и | x − 3 | будут положительными. В итоге имеем:
ln x — 1 · x — 2 x — 3 = ln ( x — 1 ) + ln x — 2 — ln x — 3 = = ln x — 1 + ln ( — ( x — 2 ) ) — ln ( — ( x — 3 ) )
Теперь объединяем получившиеся результаты.
Ответ: ln x — 1 · x — 2 x — 3 = ln x — 1 + ln ( — ( x — 2 ) ) — ln ( — ( x — 3 ) )
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
- сумма логарифмов log a | X | + log a | Y | , a > 0 , a ≠ 1 может быть использована вместо логарифма произведения log a ( X · Y ) .
- Разность логарифмов log a | X | − log a | Y | , где a > 0 , a ≠ 1 , X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p · log a | B | , где a > 0 , a ≠ 1 , p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p .
Условие: выполните упрощение выражения 13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
( x + 4 ) · ( x — 2 ) > 0 , ( x + 4 ) 13 x — 2 > 0 — ∞ , — 4 ∪ 2 , + ∞
У нас получилось, что значения выражений x + 4 , x − 2 и ( x + 4 ) 13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 ( x + 4 ) 13 x — 2 = = 13 · log 8 x + 4 + 13 · log 8 x — 2 — — log 8 x + 4 13 — log 8 x — 2 = = 13 · log 8 x + 4 + 13 · log 8 x — 2 — — log 8 ( x + 14 ) 13 + log 8 x — 2 = = 13 · log 8 x + 4 — log 8 ( x + 4 ) 13 + 14 · log 8 x — 2
Зная свойства модуля, перепишем x + 4 13 в виде x + 4 13 . Значит, что:
13 · log 8 x + 4 — log 8 ( x + 4 ) 13 + 14 · log 8 x — 2 = = 13 · log 8 x + 4 — log 8 x + 4 13 + 14 · log 8 x — 2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13 · log 8 x + 4 — log 8 x + 4 13 + 14 · log 8 x — 2 = = 13 · log 8 x + 4 — 13 · log 8 x + 4 + 14 · log 8 x — 2 = = 14 · log 8 x — 2
Возможны и другие преобразования, которые дают тот же результат:
13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 = = log 8 ( ( x + 4 ) · ( x — 2 ) ) 13 — log 8 x + 4 13 x — 2 = = log 8 ( ( x + 4 ) 13 · ( x — 2 ) ) 13 — log 8 x + 4 13 x — 2 = = log 8 ( x + 4 ) 13 · ( x — 2 ) 13 x + 4 13 x — 2 = log 8 ( x — 2 ) 14
Поскольку на области допустимых значений x − 2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log 8 ( x — 2 ) 14 = 14 · log 8 x — 2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14 · log 8 ( x − 2 ) , который был бы верен при x ∈ ( 2 , + ∞ ) , однако ошибочен на всей остальной области допустимых значений.
Ответ: 13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 = 14 · log 8 x — 2 .
Видео:Шпаргалка для школьника — Все Свойства Логарифмов за 15 минутСкачать

Как решать логарифмические уравнения подробный разбор примеров
Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Сложение и вычитание логарифмов.
Возьмем два логарифма с одинаковыми основаниями: loga x и loga y. Тогда сними возможно выполнять операции сложения и вычитания:
Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов – логарифму частного. Причем это верно если числа а, х и у положительны и а ≠ 1.
Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!
Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.
Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а, x и у положительны и а ≠ 1, то:
Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а, х и у положительны и а ≠ 1, то:
Применим вышеизложенные теоремы для решения примеров:
Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:
так как выражения log2(-8) и log2(-4) вообще не определены (логарифмическая функция у = log2х определена лишь для положительных значений аргументах).
Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x1, x2, . . . ,xn существует тождество :
Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что loga1= 0, следовательно,
А значит имеет место равенство:
Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:
Видео:Логарифмы-1. Уравнения: от базы до олимпиадСкачать

Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. 

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Видео:Логарифмы в ЕГЭ💥 Второй пример с тебя!Скачать

Два очевидных следствия определения логарифма
log a 1 = 0 ( a > 0, a ≠ 1 )
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.
Видео:Логарифмические уравнения - Как решать методом потенцированияСкачать

Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 |  | ||||||||||||||
 |  | ||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | ( формула перехода к новому основанию логарифмов ), | ||||||||||||||
 | |||||||||||||||
 |
Видео:ЛОГАРИФМЫ с нуля за 25 минут | ЕГЭ Математика | Аня Матеманя | ТопскулСкачать  Степень можно выносить за знак логарифмаИ вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример: log a ( f ( x ) 2 = 2 log a f ( x ) Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени. Логарифм произведения и логарифм частногоlog a b c = log a b − log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ. log a ( f ( x ) g ( x ) ) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля. Преобразуя данное выражение в сумму log a f ( x ) + log a g ( x ) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6). Формула перехода к новому основаниюТот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной. Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8): log a b = 1 log b a ( a > 0, a ≠ 1, b > 0, b ≠ 1 ) Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать: Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя! Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор. Запомните, что логарифм от a по основанию а всегда равен единице: loga a = 1 – это логарифмическая единица. Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1: loga 1 = 0 – логарифмический ноль. Как решать уравнения с логарифмами: 2 способа с примерамиРешить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида: При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку! Давайте посмотрим, как это работает на примере: Воспользуемся определением логарифма и получим: Теперь перед нами простейшее уравнение, решить которое не составит труда: Сделаем проверку. Подставим найденный Х в исходное уравнение: Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ. Поэтому мы покажем еще один способ решения логарифмических уравнений. Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так: Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере. Решим еще раз то же самое уравнение, но теперь этим способом: Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его: Воспользуемся этим свойством в нашем случае, получим: Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений. Разберем другой пример: Теперь делаем проверку: Еще один пример решения логарифмического уравнения:
Теперь подставим х2 = -5 в исходное уравнение: Сравнение логарифмов
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
|
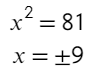
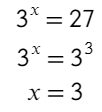
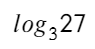
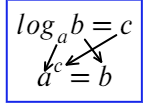
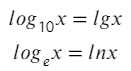
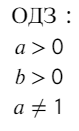
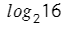
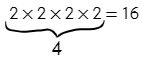
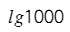
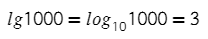
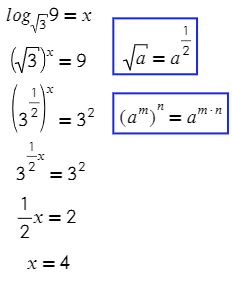
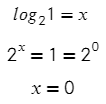
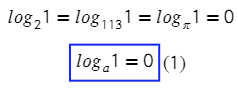
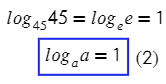
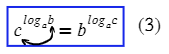
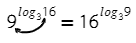
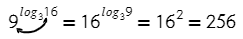
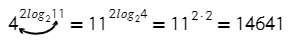
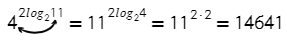
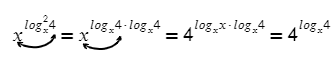
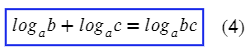
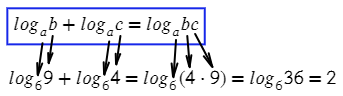
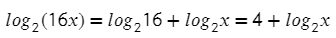
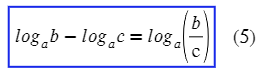
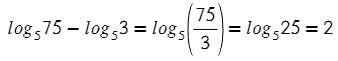
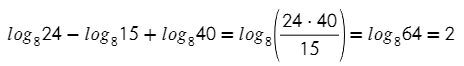
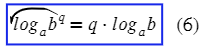
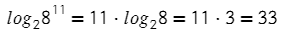
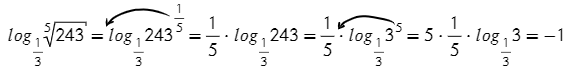
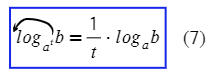
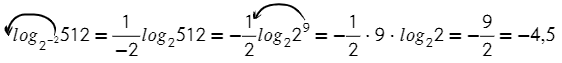
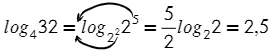
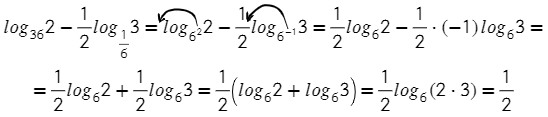
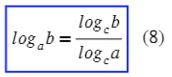
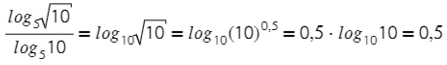
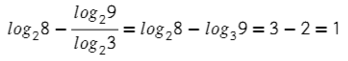
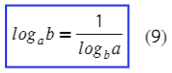
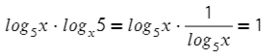
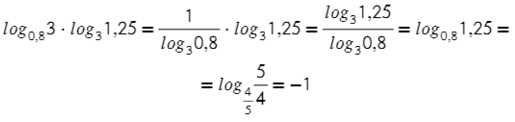
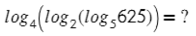
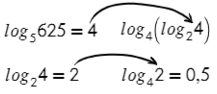
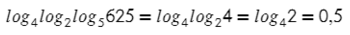
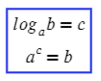
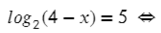
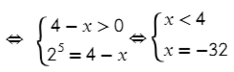
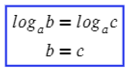
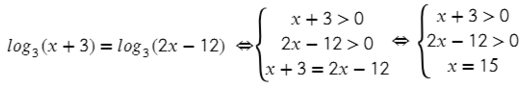
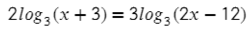
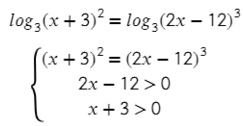
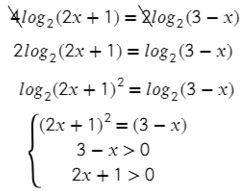
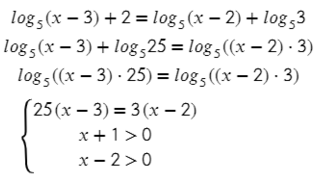
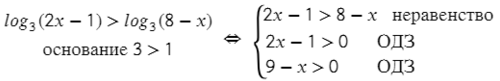

























 Логарифмы с одинаковыми основаниями можно вычитать:
Логарифмы с одинаковыми основаниями можно вычитать: 
 Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
 Вспоминаем определение логарифма и получаем следующее:
Вспоминаем определение логарифма и получаем следующее:  Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
 Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
 В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2. То есть в нашем случае:
То есть в нашем случае:  То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать: Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
 Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:
Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили: Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение: Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:  Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:  Теперь можно зачеркнуть логарифмы и тогда получим:
Теперь можно зачеркнуть логарифмы и тогда получим:  Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней:
Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней: то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
то последнее выражение верно. Следовательно, х = 3 является корнем уравнения. Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:  Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:  Выполнив преобразования правой и левой частей уравнения, мы получили:
Выполнив преобразования правой и левой частей уравнения, мы получили:  Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы: Решим данное квадратное уравнение, найдем дискриминант:
Решим данное квадратное уравнение, найдем дискриминант: Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Верно, следовательно, х1 = 1 является корнем уравнения.
Верно, следовательно, х1 = 1 является корнем уравнения. Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.








 Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.



 Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
 Применяем эти знания и получаем:
Применяем эти знания и получаем:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма: Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:
Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:  Делаем проверку:
Делаем проверку:  Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:
Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим: Верно, следовательно, х = 4 является корнем уравнения.
Верно, следовательно, х = 4 является корнем уравнения. Преобразуем правую часть уравнения:
Преобразуем правую часть уравнения:  Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:
Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:  Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы:  Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:


 Перепишем нашу систему:
Перепишем нашу систему:  Перепишем нашу систему: Следовательно, наша система примет следующий вид:
Перепишем нашу систему: Следовательно, наша система примет следующий вид:  Теперь решаем наше уравнение:
Теперь решаем наше уравнение:  Теперь решаем наше уравнение: Справа у нас квадрат суммы:
Теперь решаем наше уравнение: Справа у нас квадрат суммы: Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.