Можно ли сократить квадраты в уравнении (5 видео)

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).

5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.

Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.

1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.

Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.

Получаем, что . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.

2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.

Как, например, решить неравенство

Перенесем все в левую часть неравенства, чтобы в правой остался ноль.

Разложим левую часть на множители.

Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: .

Запомним: ответы типа « > » абсурдны.

Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .

4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.

5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.

6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.

При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.

Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.

А теперь – полезный лайфхак для решения дробно-рациональных неравенств.

Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.

Может быть, сделаем проще? Представим дробь в виде суммы дробей и .

Продолжаем упрощать левую часть:

Теперь можно и привести дроби к одному знаменателю.

Все, больше ничего не пишем. Решаем неравенство методом интервалов.

Содержание

Формулы сокращённого умножения
Квадрат суммы двух выражений
Квадрат разности двух выражений
Куб суммы и куб разности
Умножение разности двух выражений на их сумму
Умножение разности двух выражений на неполный квадрат их суммы
Умножение суммы двух выражений на неполный квадрат их разности
Можно ли сократить квадраты в уравнении
🎬 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Формулы сокращённого умножения

Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.

Видео:Сократить дробь алгебра 8 классСкачать

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y) 2 .

Выражение (2x + 3y) 2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

То есть выражение (2x + 3y) 2 равно 4x 2 + 12xy + 9y 2

Решим аналогичный пример, который попроще:

Выражение (a + b) 2 это перемножение двух многочленов, каждый из которых равен (a + b)

Выполним это умножение:

То есть выражение (a + b) 2 равно a 2 + 2ab + b 2

Оказывается, что случай (a + b) 2 можно распространить для любых a и b . Первый пример, который мы решили, а именно (2x + 3y) 2 можно решить с помощью тождества (a + b) 2 = a 2 + 2ab + b 2 . Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y) 2 . В данном случае переменной a соответствует член 2x , а переменной b соответствует член 3y

И далее можно воспользоваться тождеством (a + b) 2 = a 2 + 2ab + b 2 , но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

Как и в прошлый раз получили многочлен 4x 2 + 12xy + 9y 2 . Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

Тождество (a + b) 2 = a 2 + 2ab + b 2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3) 2 . Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3) 2 = 5 2 = 25

Второй способ:

(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3) 2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(5a + 3) 2 = (5a) 2 + 2 × 5a × 3 + 3 2 = 25a 2 + 30a + 9

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

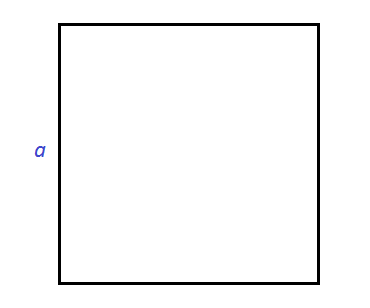
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a 2 . Если увеличить сторону квадрата на b , то площадь будет равна (a + b) 2

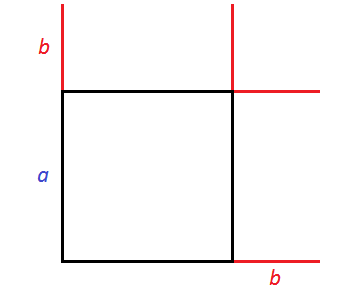
Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b . У квадрата все стороны равны. Если его сторону увеличить на b , то остальные стороны тоже увеличатся на b

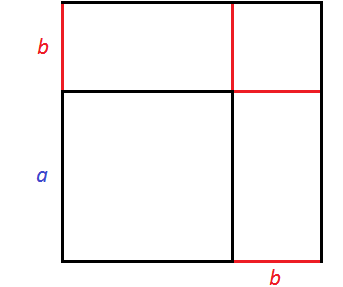
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

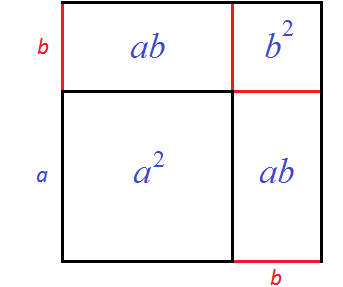
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a 2 . Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab . Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab , которое буквально будет означать «повторить два раза площадь прямоугольника ab» . Алгебраически это получается путём приведения подобных слагаемых ab и ab . В результате получается выражение a 2 + 2ab + b 2 , которое является правой частью формулы квадрата суммы двух выражений:

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b) 2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)

Если выполнить это умножение, то получится многочлен a 2 − 2ab + b 2

Пример 1. Преобразовать выражение (7x − 5) 2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(7x − 5) 2 = (7x) 2 − 2 × 7x × 5 + 5 2 = 49x 2 − 70x + 25

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a 2 , то площадь квадрата, сторона которого уменьшена на b , будет равна (a − b) 2

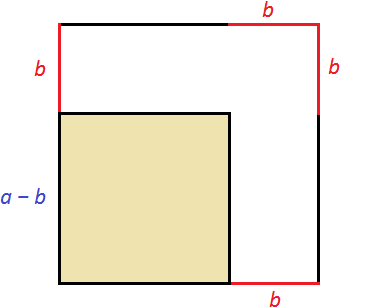
Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b . У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

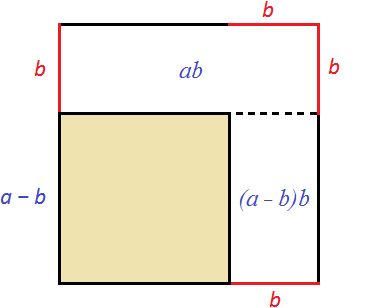
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b , поскольку старая сторона a уменьшилась на b . Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a 2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a 2 минус площадь ab минус площадь (a − b)b

Раскроем скобки в выражении (a − b)b

Приведем подобные слагаемые:

В результате получается выражение a 2 − 2ab + b 2 , которое является правой частью формулы квадрата разности двух выражений:

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y) 2 , и мы хотим воспользоваться формулой (a − b) 2 = a 2 − 2ab + b 2 , то вместо b нужно подставлять 2y , а не −2y . Это особенность работы с формулами, которую не следует забывать.

Если подставлять −2y , то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

Исключением могут быть выражения вида (x − (−y)) 2 . В данном случае, применяя формулу (a − b) 2 = a 2 − 2ab + b 2 вместо b следует подставить (−y)

Но возводя в квадрат выражения вида x − (−y) , удобнее будет заменять вычитание на сложение x + y . Тогда первоначальное выражение примет вид (x + y) 2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

Выражение (a + b) 3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)

Но выражение (a + b) 3 также может быть записано как (a + b)(a + b) 2

При этом сомножитель (a + b) 2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a 2 + 2ab + b 2 .

А это есть умножение многочлена на многочлен. Выполним его:

Аналогично можно вывести формулу куба разности двух выражений:

Пример 1. Преобразуйте выражение (x + 1) 3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(x + 1) 3 = x 3 + 3 × x 2 × 1 + 3 × x × 1 2 + 1 3 = x 3 + 3x 2 + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:

Пример 2. Преобразовать выражение (6a 2 + 3b 3 ) 3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(6a 2 + 3b 3 ) 3 = (6a 2 ) 3 + 3 × (6a 2 ) 2 × 3b 3 + 3 × 6a 2 × (3b 3 ) 2 + (3b 3 ) 3 = 216a 6 + 3 × 36a 4 × 3b 3 + 3 × 6a 2 × 9b 6 + 27b 9

Пример 3. Преобразовать выражение (n 2 − 3) 3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(n 2 − 3) 3 = (n 2 ) 3 − 3 × (n 2 ) 2 × 3 + 3 × n 2 × 3 2 − 3 3 = n 6 − 9n 4 + 27n 2 − 27

Пример 4. Преобразовать выражение (2x 2 − x 3 ) 3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

То есть выражение (a − b)(a + b) равно a 2 − b 2

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b)(a + b) можно распространить для любых a и b . Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1. Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a 2 − b 2 имеем:

Вычислим правую часть, получим 4x 2 − 25

Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a 2 − b 2 . У нас получится тот же результат 4x 2 − 25

Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)

Воспользуемся формулой умножения разности двух выражений на их сумму:

Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)

Воспользуемся формулой умножения разности двух выражений на их сумму:

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a 2 − b 2 разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b) , так и (a + b)(a − b) . Результат по прежнему будет равен a 2 − b 2 , поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b) , так и (2a − 3b)(2a + 3b) . Результат всё так же будет равен 4a 2 − 9b 2 .

Пример 3. Выполнить умножение (7 + 3x)(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

Пример 4. Выполнить умножение (x 2 − y 3 )(x 2 + y 3 )

Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)

В выражении (−5x − 3y) вынесем за скобки −1 , тогда исходное выражение примет следующий вид:

Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x) 2 . А это приведет к ошибке и изменению значения исходного выражения.

Далее вычисляем выражение в скобках:

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

Видео:7 класс, 24 урок, Формулы сокращённого умноженияСкачать

Умножение разности двух выражений на неполный квадрат их суммы

Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:

Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a 2 + ab + b 2 ) является неполным квадратом суммы этих двух выражений.

Неполный квадрат суммы это многочлен вида a 2 + ab + b 2 . Он похож на обычный квадрат суммы a 2 + 2ab + b 2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x 2 + 6xy + 9y 2 является неполным квадратом суммы выражений 2x и 3y .

Действительно, первый член выражения 4x 2 + 6xy + 9y 2 , а именно 4x 2 является квадратом выражения 2x , поскольку (2x) 2 = 4x 2 . Третий член выражения 4x 2 + 6xy + 9y 2 , а именно 9y 2 является квадратом выражения 3y , поскольку (3y) 2 = 9y 2 . Член находящийся в середине 6xy , является произведением выражений 2x и 3y.

Итак, умножим разность (a − b) на неполный квадрат суммы a 2 + ab + b 2

Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

Пример 1. Выполнить умножение (2x − 3y)(4x 2 + 6xy + 9y 2 )

Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y . Второй многочлен 4x 2 + 6xy + 9y 2 это неполный квадрат суммы двух выражений 2x и 3y . Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a 2 + ab + b 2 ) = a 3 − b 3 . В нашем случае умножение (2x − 3y)(4x 2 + 6xy + 9y 2 ) можно заменить на разность кубов 2x и 3y

Попробуем решить этот же пример, не пользуясь формулой (a − b)(a 2 + ab + b 2 ) = a 3 − b 3 . У нас получится тот же результат, но решение станет длиннее:

Пример 2. Выполнить умножение (3 − x)(9 + 3x + x 2 )

Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a 2 + ab + b 2 ) = a 3 − b 3

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Умножение суммы двух выражений на неполный квадрат их разности

Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:

Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a 2 − ab + b 2 ) является неполным квадратом разности этих двух выражений.

Неполный квадрат разности это многочлен вида a 2 − ab + b 2 . Он похож на обычный квадрат разности a 2 − 2ab + b 2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x 2 − 6xy + 9y 2 является неполным квадратом разности выражений 2x и 3 y .

Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a 2 − ab + b 2

Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

Пример 1. Выполнить умножение (2x + 3y)(4x 2 − 6xy + 9y 2 )

Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y , а второй многочлен 4x 2 − 6xy + 9y 2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a 2 − ab + b 2 ) = a 3 + b 3 . В нашем случае умножение (2x + 3y)(4x 2 − 6xy + 9y 2 ) можно заменить на сумму кубов 2x и 3y

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a 2 − ab + b 2 ) = a 3 + b 3 . У нас получится тот же результат, но решение станет длиннее:

Пример 2. Выполнить умножение (2x + y)(4x 2 − 2xy + y 2 )

Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x 2 − 2xy + y 2 ) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a 2 − ab + b 2 ) = a 3 + b 3

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Можно ли сократить квадраты в уравнении

РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ

§ 4. Дополнительные замечания о решении уравнений.

Выше было сказано, что обе части уравнения можно умножать или делить на одно и то же количество. Говоря это, мы понимаем возможность этих действий в том смысле, что, производя их над данным уравнением, мы получаем новое уравнение, совместное с данным. Заметим теперь, что это указание верно только в том случае, когда множитель или делитель есть или явное количество, или хотя и неявное, но не содержит в себе той самой неизвестной буквы, которая входит в уравнение. Если дано выражение, содержащее то же неизвестное, как и в уравнении, то, вообще говоря, нельзя ни помножать уравнение на это выражение, ни делить на него. Поясним это на примерах:

Возьмем уравнение х = 2, которое очевидно имеет один только корень 2. Если мы умножим обе части его на х, то новое уравнение х 2 =2х не будет уже совместно с данным, потому что кроме прежнего корня 2, оно будет иметь еще корень 0, что обнаруживается и прямо из самаго уравнения, а также при решении полученного уравнения, если заменить его уравнением х 2 —2х=0 и написать последное в виде х(х—2)=0. Подобно этому, умножая данное уравнение х = 2 на выражение х—1, получаем новое уравнение
х 2 —2х=2х —2, совместное с уравнением (х—1)(х—2)=0 и имеющее два корня, прежний 2 и новый 1. Вообще при умножении уравнения на выражение, содержащее неизвестное, в это уравнение вводятся посторонние корни, а именно те, которые обращают множитель в нуль.

ІІонятно, наоборот, что если мы имеем, напр., уравнение х 2 =3х , корни которого суть 0 и 3 и сократим его на х, то полученное от этого сокращеиия уравнение не будет совместно с данным, потому что оно имеет только один корень 3. Подобно этому, имея уравнение (х—2) 2 =2х—4, корни которого суть 2 и 4, и сократив обе части на х—2, мы теряем корень 2 и получаем уравнение х—2 = 2, имеющее только один корень 4. Вообще при со-кращении обеих частей уравнения на их общий множитель, содержащий неизвестное, теряются корни уравнения и именно те, которые обращают делитель в нуль.

В курсе алгебры доказывается, что уравнение можно умножать на множитель, содержащий неизвестное, только в том случае, когда этот множитель входит в знаменатель дроби, получившейся от соединения всех дробей, входящих в уравнение, в одну дробь, и после окончательного сокращения этой последней.Так, если уравнение имеет вид А+ В /_С=0, где А есть совокупность всех целых членов, а В /_С есть несократимая дробь, то, умножая на С, получим уравнение АС+В=0, совместное с данным. В противном случае, если дробь В /_С сократима, то необходимо сократить ее раньше уничтожения ее знаменателя, чтобы не внести в уравнение постороннего ему корня.

Обратно, только тогда можно разделить обе части уравнения на выражение, содержащее неизвестное, когда от этого получатся такие дроби, которые, будучи соединены все в одной части уравнения, дают в результате дробь, не сокращающуюся ни на какой множитель, содержащий неизвестное. В противном случае нужно при сокращении уравнения на делитель, заметить тот корень, который теряется при этом сокращении, и считать его в числе корней данного уравнения.

В нижеследующих задачах звездочкой обозначены те уравнения, при решении которых нужно принимать во внимаиие сделанные выше указания. Остальные задачи можно решать по обыкновенным правилам.