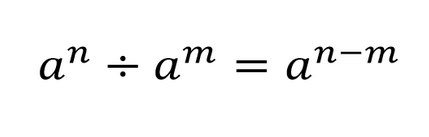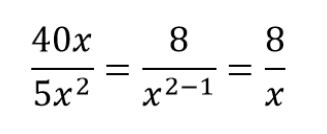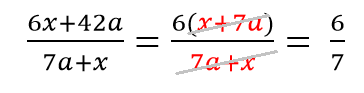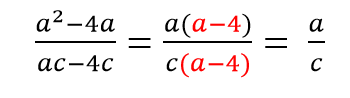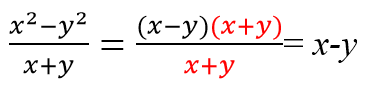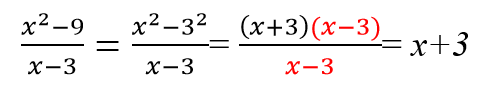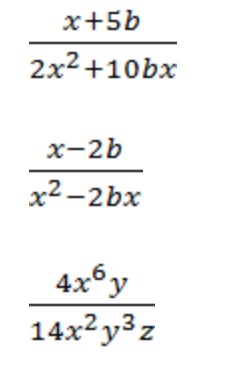РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ
§ 4. Дополнительные замечания о решении уравнений.
Выше было сказано, что обе части уравнения можно умножать или делить на одно и то же количество. Говоря это, мы понимаем возможность этих действий в том смысле, что, производя их над данным уравнением, мы получаем новое уравнение, совместное с данным. Заметим теперь, что это указание верно только в том случае, когда множитель или делитель есть или явное количество, или хотя и неявное, но не содержит в себе той самой неизвестной буквы, которая входит в уравнение. Если дано выражение, содержащее то же неизвестное, как и в уравнении, то, вообще говоря, нельзя ни помножать уравнение на это выражение, ни делить на него. Поясним это на примерах:
Возьмем уравнение х = 2, которое очевидно имеет один только корень 2. Если мы умножим обе части его на х, то новое уравнение х 2 =2х не будет уже совместно с данным, потому что кроме прежнего корня 2, оно будет иметь еще корень 0, что обнаруживается и прямо из самаго уравнения, а также при решении полученного уравнения, если заменить его уравнением х 2 —2х=0 и написать последное в виде х(х—2)=0. Подобно этому, умножая данное уравнение х = 2 на выражение х—1, получаем новое уравнение
х 2 —2х=2х —2, совместное с уравнением (х—1)(х—2)=0 и имеющее два корня, прежний 2 и новый 1. Вообще при умножении уравнения на выражение, содержащее неизвестное, в это уравнение вводятся посторонние корни, а именно те, которые обращают множитель в нуль.
ІІонятно, наоборот, что если мы имеем, напр., уравнение х 2 =3х , корни которого суть 0 и 3 и сократим его на х, то полученное от этого сокращеиия уравнение не будет совместно с данным, потому что оно имеет только один корень 3. Подобно этому, имея уравнение (х—2) 2 =2х—4, корни которого суть 2 и 4, и сократив обе части на х—2, мы теряем корень 2 и получаем уравнение х—2 = 2, имеющее только один корень 4. Вообще при со-кращении обеих частей уравнения на их общий множитель, содержащий неизвестное, теряются корни уравнения и именно те, которые обращают делитель в нуль.
В курсе алгебры доказывается, что уравнение можно умножать на множитель, содержащий неизвестное, только в том случае, когда этот множитель входит в знаменатель дроби, получившейся от соединения всех дробей, входящих в уравнение, в одну дробь, и после окончательного сокращения этой последней.Так, если уравнение имеет вид А+ В /С=0, где А есть совокупность всех целых членов, а В /С есть несократимая дробь, то, умножая на С, получим уравнение АС+В=0, совместное с данным. В противном случае, если дробь В /С сократима, то необходимо сократить ее раньше уничтожения ее знаменателя, чтобы не внести в уравнение постороннего ему корня.
Обратно, только тогда можно разделить обе части уравнения на выражение, содержащее неизвестное, когда от этого получатся такие дроби, которые, будучи соединены все в одной части уравнения, дают в результате дробь, не сокращающуюся ни на какой множитель, содержащий неизвестное. В противном случае нужно при сокращении уравнения на делитель, заметить тот корень, который теряется при этом сокращении, и считать его в числе корней данного уравнения.
В нижеследующих задачах звездочкой обозначены те уравнения, при решении которых нужно принимать во внимаиие сделанные выше указания. Остальные задачи можно решать по обыкновенным правилам.
- Как сокращать алгебраические дроби?
- Определение
- Сокращение алгебраических дробей
- Сокращение алгебраических дробей с многочленами
- Вынесение общего множителя при сокращении дробей
- Сокращение дробей. Формулы сокращенного умножения
- Сокращение алгебраических дробей: правило, примеры.
- Смысл сокращения алгебраической дроби
- Все ли алгебраические дроби подлежат сокращению?
- Правило сокращения алгебраических дробей
- Характерные примеры
- 📺 Видео
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как сокращать алгебраические дроби?
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
- Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
- Всегда делим на наименьшее значение в степени
- Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
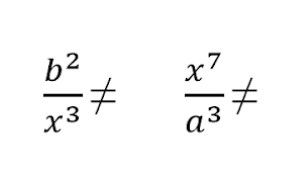 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
- Общий множитель для числителя и знаменателя — 8.
- Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
- Общий множитель для числителя и знаменателя — 7.
- b 3 и b делим на b.
- Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
- сокращайте многочлен в скобках только с таким же многочленом в скобках;
- сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
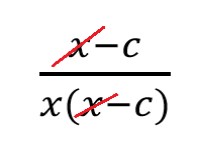 | 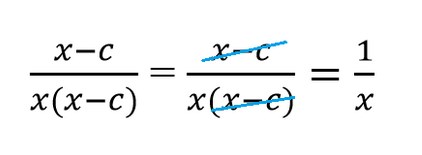 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
- Найдите число, на которое делятся числа каждого одночлена.
- Найдите повторяющиеся буквенные множители в каждом одночлене.
- Вынесите найденные буквенные множители за скобку.
- Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
- Выносим общий множитель 6
- Делим 42/6
- Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Сократить дробь алгебра 8 классСкачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
- Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
- Поделите числитель и знаменатель на общий множитель.
- Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
- Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
- Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
- Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
- Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Сокращение алгебраических дробей: правило, примеры.
Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.
Видео:Решение уравнений с помощью разложения на множители.Скачать
Смысл сокращения алгебраической дроби
В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Сокращение алгебраической дроби представляет собой аналогичное действие.
Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.
К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х , и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .
Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.
Видео:Разложение кубических выражений на множителиСкачать

Все ли алгебраические дроби подлежат сокращению?
Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .
С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .
В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х , или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.
Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Правило сокращения алгебраических дробей
Правило сокращения алгебраических дробей состоит из двух последовательных действий:
- нахождение общих множителей числителя и знаменателя;
- в случае нахождения таковых осуществление непосредственно действия сокращения дроби.
Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.
Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .
Видео:РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

Характерные примеры
Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:
5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ;
Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105
Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105
(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105
По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.
Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение.
Решение
Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:
— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6
Однако, более рациональным способом будет запись решения в виде выражения со степенями:
— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .
Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6
Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.
Решение
Возможно сократить дробь таким образом:
2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2
Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК ( 5 , 10 ) = 10 . Тогда получим:
2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .
Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2
Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить.
Решение
Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 )
Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:
2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 ) = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 )
Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · ( a + 7 ) . Произведем сокращение:
2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b
Краткое решение без пояснений запишем как цепочку равенств:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 a + 49 ) b 3 · ( a 2 — 49 ) = = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b
Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .
Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.
Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.
Решение
На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:
1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2
Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:
x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10
Теперь становится виден общий множитель, осуществляем сокращение:
— 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x
Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x .
Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.
📺 Видео
Алгебра 8. Урок 2 - Сокращение дробейСкачать

Как решают уравнения в России и СШАСкачать

Квадратный трехчлен . Сократить дробь.Скачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Формулы сокращенного умножения | Математика | TutorOnlineСкачать

Как решать уравнения с дробью? #shortsСкачать

Ошибки при сокращении дробей.Скачать

Математика 5 класс. 28 октября. Вынесение множителя за скобки в уравнениях #2Скачать