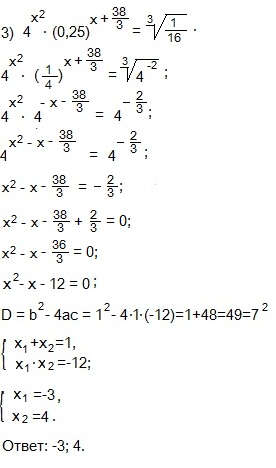Можно ли опустить квадрат в уравнении (7 видео)

Содержание

Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, приводимые к квадратным на примерах
Уравнение 1
Уравнение 2
Уравнение 3
Можно ли опустить квадрат в уравнении
Решение неравенств: основные ошибки и полезные лайфхаки
💡 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Показательные уравнения, сводящиеся к квадратным

Разберем показательные уравнения, сводящиеся к квадратным. Их могут ученики кратко называть «квадратные показательные уравнения», хотя это название не точное. Однако, многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax 2 +bx+c=0.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Показательные уравнения, приводимые к квадратным на примерах

Уравнение 1

Решить уравнение:

1) 4 x +2 x+1 -3=0. Представим 4 x в виде степени с основанием 2.

(2 2 ) x +2 x ∙2 1 -3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:

вводим новую переменную: пусть 2 x =y;

y 2 + 2 y -3 =0.

Дискриминант для четного второго коэффициента: D₁=1 2 -1∙(-3)=1+3=4=2 2 – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Возвращаемся к переменной х:

1) 2 x =-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).

2) 2 x = 1. Число 1 можно представлять в виде нулевой степени по любому основанию.

2 x = 2 0 ;

Уравнение 2

2) 0,25 2x -5∙0,5 2x +4=0. Решаем аналогично. Представляем 0,25 2x — в виде степени с основанием 0,5.

(0,5 2 ) 2x -5∙0,5 2x +4=0;

(0,5 2x ) 2 -5∙0,5 2x +4=0.

0,5 2x =y; ввели новую переменную у и получили приведенное квадратное уравнение:

y 2 — 5 y+ 4 =0;

Дискриминант D=b 2 -4ac=5 2 -4∙1∙4=25-16=9=3 2 — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂= 5 , y₁+y₂= 4 . Корни приведенного квадратного уравнения находим подбором: y₁=1, y₂=4 и возвращаемся к переменной х:

1) 0,5 2x = 1 ; число 1 можно представлять в виде нулевой степени по любому основанию.

0,5 2x = 0,5 0 ;

2) 0,5 2 x =4; приведем степень 0,5 2 x к основанию 2, применив формулу: (1/a) x =а -х

2 -2 x =2 2 ; приравниваем показатели:

Уравнение 3

Представим левую и правую части в виде степеней с основанием 4, используя формулы: а -х =1/a x и a x ∙a y =a x + y .

Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.

Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Итак, решение показательных уравнений, которое мы разбирали в предыдущем уроке, пополнилось еще одним методом — приведением показательного уравнения к обычному квадратному уравнению. Такие уравнения называют — показательные уравнения, сводящиеся к квадратным.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Можно ли опустить квадрат в уравнении

РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ

§ 4. Дополнительные замечания о решении уравнений.

Выше было сказано, что обе части уравнения можно умножать или делить на одно и то же количество. Говоря это, мы понимаем возможность этих действий в том смысле, что, производя их над данным уравнением, мы получаем новое уравнение, совместное с данным. Заметим теперь, что это указание верно только в том случае, когда множитель или делитель есть или явное количество, или хотя и неявное, но не содержит в себе той самой неизвестной буквы, которая входит в уравнение. Если дано выражение, содержащее то же неизвестное, как и в уравнении, то, вообще говоря, нельзя ни помножать уравнение на это выражение, ни делить на него. Поясним это на примерах:

Возьмем уравнение х = 2, которое очевидно имеет один только корень 2. Если мы умножим обе части его на х, то новое уравнение х 2 =2х не будет уже совместно с данным, потому что кроме прежнего корня 2, оно будет иметь еще корень 0, что обнаруживается и прямо из самаго уравнения, а также при решении полученного уравнения, если заменить его уравнением х 2 —2х=0 и написать последное в виде х(х—2)=0. Подобно этому, умножая данное уравнение х = 2 на выражение х—1, получаем новое уравнение
х 2 —2х=2х —2, совместное с уравнением (х—1)(х—2)=0 и имеющее два корня, прежний 2 и новый 1. Вообще при умножении уравнения на выражение, содержащее неизвестное, в это уравнение вводятся посторонние корни, а именно те, которые обращают множитель в нуль.

ІІонятно, наоборот, что если мы имеем, напр., уравнение х 2 =3х , корни которого суть 0 и 3 и сократим его на х, то полученное от этого сокращеиия уравнение не будет совместно с данным, потому что оно имеет только один корень 3. Подобно этому, имея уравнение (х—2) 2 =2х—4, корни которого суть 2 и 4, и сократив обе части на х—2, мы теряем корень 2 и получаем уравнение х—2 = 2, имеющее только один корень 4. Вообще при со-кращении обеих частей уравнения на их общий множитель, содержащий неизвестное, теряются корни уравнения и именно те, которые обращают делитель в нуль.

В курсе алгебры доказывается, что уравнение можно умножать на множитель, содержащий неизвестное, только в том случае, когда этот множитель входит в знаменатель дроби, получившейся от соединения всех дробей, входящих в уравнение, в одну дробь, и после окончательного сокращения этой последней.Так, если уравнение имеет вид А+ В /_С=0, где А есть совокупность всех целых членов, а В /_С есть несократимая дробь, то, умножая на С, получим уравнение АС+В=0, совместное с данным. В противном случае, если дробь В /_С сократима, то необходимо сократить ее раньше уничтожения ее знаменателя, чтобы не внести в уравнение постороннего ему корня.

Обратно, только тогда можно разделить обе части уравнения на выражение, содержащее неизвестное, когда от этого получатся такие дроби, которые, будучи соединены все в одной части уравнения, дают в результате дробь, не сокращающуюся ни на какой множитель, содержащий неизвестное. В противном случае нужно при сокращении уравнения на делитель, заметить тот корень, который теряется при этом сокращении, и считать его в числе корней данного уравнения.

В нижеследующих задачах звездочкой обозначены те уравнения, при решении которых нужно принимать во внимаиие сделанные выше указания. Остальные задачи можно решать по обыкновенным правилам.

Видео:НУБ И ПРО ПОСТРОИЛИ ЗАЩИЩЕННЫЙ ДОМ ПРОТИВ ИНОПЛАНЕТЯН НА ЛУНЕ МАЙНКРАФТ ! НУБИК ЛОВУШКА MINECRAFTСкачать

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).

5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.

Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.

1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.

Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.

Получаем, что . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.

2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.

Как, например, решить неравенство

Перенесем все в левую часть неравенства, чтобы в правой остался ноль.

Разложим левую часть на множители.

Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: .

Запомним: ответы типа « > » абсурдны.

Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .

4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.

5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.

6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.

При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.

Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.

А теперь – полезный лайфхак для решения дробно-рациональных неравенств.

Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.

Может быть, сделаем проще? Представим дробь в виде суммы дробей и .

Продолжаем упрощать левую часть:

Теперь можно и привести дроби к одному знаменателю.

Все, больше ничего не пишем. Решаем неравенство методом интервалов.