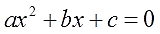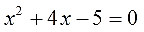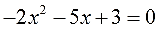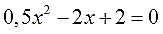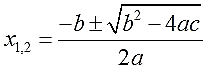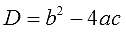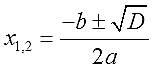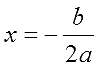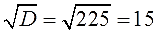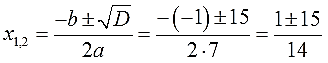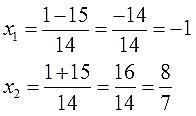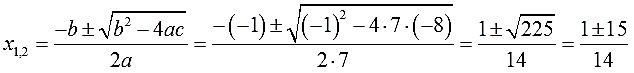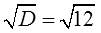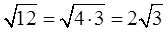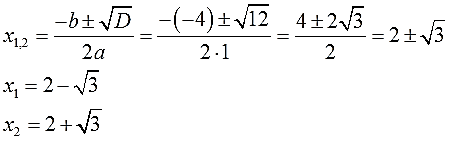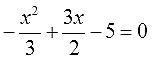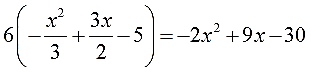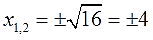РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ
§ 4. Дополнительные замечания о решении уравнений.
Выше было сказано, что обе части уравнения можно умножать или делить на одно и то же количество. Говоря это, мы понимаем возможность этих действий в том смысле, что, производя их над данным уравнением, мы получаем новое уравнение, совместное с данным. Заметим теперь, что это указание верно только в том случае, когда множитель или делитель есть или явное количество, или хотя и неявное, но не содержит в себе той самой неизвестной буквы, которая входит в уравнение. Если дано выражение, содержащее то же неизвестное, как и в уравнении, то, вообще говоря, нельзя ни помножать уравнение на это выражение, ни делить на него. Поясним это на примерах:
Возьмем уравнение х = 2, которое очевидно имеет один только корень 2. Если мы умножим обе части его на х, то новое уравнение х 2 =2х не будет уже совместно с данным, потому что кроме прежнего корня 2, оно будет иметь еще корень 0, что обнаруживается и прямо из самаго уравнения, а также при решении полученного уравнения, если заменить его уравнением х 2 —2х=0 и написать последное в виде х(х—2)=0. Подобно этому, умножая данное уравнение х = 2 на выражение х—1, получаем новое уравнение
х 2 —2х=2х —2, совместное с уравнением (х—1)(х—2)=0 и имеющее два корня, прежний 2 и новый 1. Вообще при умножении уравнения на выражение, содержащее неизвестное, в это уравнение вводятся посторонние корни, а именно те, которые обращают множитель в нуль.
ІІонятно, наоборот, что если мы имеем, напр., уравнение х 2 =3х , корни которого суть 0 и 3 и сократим его на х, то полученное от этого сокращеиия уравнение не будет совместно с данным, потому что оно имеет только один корень 3. Подобно этому, имея уравнение (х—2) 2 =2х—4, корни которого суть 2 и 4, и сократив обе части на х—2, мы теряем корень 2 и получаем уравнение х—2 = 2, имеющее только один корень 4. Вообще при со-кращении обеих частей уравнения на их общий множитель, содержащий неизвестное, теряются корни уравнения и именно те, которые обращают делитель в нуль.
В курсе алгебры доказывается, что уравнение можно умножать на множитель, содержащий неизвестное, только в том случае, когда этот множитель входит в знаменатель дроби, получившейся от соединения всех дробей, входящих в уравнение, в одну дробь, и после окончательного сокращения этой последней.Так, если уравнение имеет вид А+ В /С=0, где А есть совокупность всех целых членов, а В /С есть несократимая дробь, то, умножая на С, получим уравнение АС+В=0, совместное с данным. В противном случае, если дробь В /С сократима, то необходимо сократить ее раньше уничтожения ее знаменателя, чтобы не внести в уравнение постороннего ему корня.
Обратно, только тогда можно разделить обе части уравнения на выражение, содержащее неизвестное, когда от этого получатся такие дроби, которые, будучи соединены все в одной части уравнения, дают в результате дробь, не сокращающуюся ни на какой множитель, содержащий неизвестное. В противном случае нужно при сокращении уравнения на делитель, заметить тот корень, который теряется при этом сокращении, и считать его в числе корней данного уравнения.
В нижеследующих задачах звездочкой обозначены те уравнения, при решении которых нужно принимать во внимаиие сделанные выше указания. Остальные задачи можно решать по обыкновенным правилам.
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать
Как решать квадратные уравнения?
Что такое квадратное уравнение? Виды квадратных уравнений. Примеры.
Обычно квадратные уравнения — одна из самых любимых учениками тем школьной математики. Почему? Потому, что алгоритм решения любого квадратного уравнения достаточно прост и универсален. Работает безотказно. Однако простора для дурацких ошибок при решении квадратных уравнений тоже хватает, да… Так что будем разбираться, что к чему.)
Начнём с названия.
Ключевым словом в понятии квадратное уравнение является слово «квадратное». Что оно означает? Оно означает то, что в уравнении обязательно должен присутствовать икс в квадрате. В любом случае. Также в уравнении могут быть (или не быть — как уж повезёт) просто икс (в первой степени) и просто число (свободный член). Но это ещё не всё. При этом в уравнении не должно быть иксов в кубе, в четвёртой и любых других степенях, больших двойки.
В самом общем виде квадратное уравнение выглядит так:
Здесь a, b, c — какие-то числа. Любые.) Числа b и c могут быть совсем-совсем любыми, а вот а — любым числом, кроме нуля. Почему — объясню чуть ниже.
В этих уравнениях слева присутствует полный набор слагаемых: есть икс в квадрате (с коэффициентом a), есть просто икс (с коэффициентом b), а также есть свободный член c. Такие квадратные уравнения в математике так и называются — полными.
А ещё бывают и такие квадратные уравнения, где чего-то не хватает. Что у нас произойдёт, если, например, обнулить коэффициент b (b=0)? У нас исчезнет икс в первой степени.
Получится, к примеру, что-то типа:
А если c=0? Тогда у нас пропадёт свободный член:
А если уж оба коэффициента a и b станут равны нулю, то тогда совсем всё просто получится:
Такие квадратные уравнения, где какого-то из членов не хватает, называются (вы не поверите) неполными.)
Таким образом, квадратные уравнения бывают двух основных видов — полные и неполные.
А теперь ответ на вопрос, почему коэффициент a не может быть равен нулю. А давайте подумаем, что у нас произойдёт, если мы обнулим коэффициент а? Да! У нас пропадёт икс в квадрате! Наше уравнение превратится в линейное . И решаться будет уже совсем по-другому…
Общая формула корней квадратного уравнения.
Квадратные уравнения решаются достаточно просто. По одной единственной универсальной формуле. Всего одной!
И теперь у меня для вас есть две новости — хорошая и плохая. С какой начнём? Принято с плохой начинать? Что ж, ладно…
Новость плохая. Строгий аналитический вывод общей формулы корней квадратного уравнения достаточно громоздок и основан на процедуре выделения полного квадрата. В большинстве школьных учебников вывод общей формулы корней всё-таки приводят, но я считаю что эта процедура — очередной вынос мозга простому среднестатистическому школьнику. Поэтому в данном уроке я его (вывод) всё-таки опущу.)
Новость хорошая. Запоминать аналитический вывод формулы корней квадратного уравнения в общем виде и не требуется. Вообще! Гораздо важнее запомнить саму формулу и научиться её применять на практике. Вот мы и попрактикуемся. И уравнения порешаем.)
«Формула! Где формула?! Ты достал формулу?» — слышу громкие возгласы, как в старом добром рекламном ролике начала 2000-х…
Достаю, достаю! Из широких штанин… О-па! Вот она, формула!)
Вот такая формула. Да, я не спорю, довольно громоздкая. Но и уравнение мы решаем всё-таки квадратное, а не более простое линейное…
Как вы видите, для поиска корней квадратного уравнения нам необходимы только коэффициенты a, b, c. И всё. Больше ничего. Аккуратно подставляем все коэффициенты в формулу и считаем наши корни.
Что такое дискриминант? Формула и смысл дискриминанта.
Выражение b 2 -4ac, стоящее в формуле под знаком квадратного корня, называется дискриминант. До боли знакомое и родное слово для большинства старшеклассников. Слова «решаем через дискриминант» звучат обнадёживающе и вселяют оптимизм!)
Обычно дискриминант обозначается буковкой D:
Тогда, с учётом данного обозначения, общая формула корней станет выглядеть вот так:
Сам по себе дискриминант, как правило, прост и безотказен в обращении. Но… В чём его смысл? Почему для, скажем, —b или 2a не вводятся какие-то специальные термины и обозначения? Буквы — они и в Африке буквы… А тут — такое красивое слово! Дискриминант…
А дело вот в чём. При решении любого квадратного уравнения по общей формуле возможны всего три ситуации.
1. Дискриминант положительный (D>0).
Это означает, что из него можно извлечь корень. Красиво корень извлекается или некрасиво — вопрос другой. Главное, что извлекается в принципе.
Тогда наше квадратное уравнение всегда имеет два различных корня.
Два — потому, что общая формула в этой ситуации разбивается на два отдельных случая. А именно — какой знак, плюс или минус, берётся перед радикалом. Каждый случай даёт свой корень.
2. Дискриминант равен нулю (D=0)
Как вы думаете, чему в этом случае будет равен корень из дискриминанта? Нулю, конечно же! А поскольку от прибавления/вычитания нуля в числителе ничего не меняется, то наше уравнение имеет один корень:
Вообще, строго говоря, это не один корень, а два одинаковых. Но в упрощённом виде, когда нам надо просто решить уравнение и получить ответ, принято говорить об одном решении. Поэтому в ответе не заморачиваются и пишут просто одинокий икс, безо всякой индексации х1,2 .
Однако в более солидных темах (например, в решении неравенств методом интервалов ) этот пунктик, с двумя одинаковыми (или, по-научному, кратными) корнями, настолько важен, что я буду про него напоминать снова и снова.
3. Дискриминант отрицательный (D
Из отрицательных чисел извлекать квадратный корень в средней школе не учат. Это означает, что уравнение не имеет корней. Ну и ладно. На нет, как говорится, и суда нет.
Как решать квадратные уравнения?
Начнём с полных квадратных уравнений.
Полные квадратные уравнения
Полное квадратное уравнение (любое!) решается всегда в четыре основных этапа.
1. Приводим уравнение к стандартному виду:
Всё просто: выстраиваем левую часть уравнения по убыванию степеней икса. На первом месте пишем слагаемое с иксом в квадрате, на втором месте — с иксом в первой степени и, наконец, свободный член. Справа — обязательно должен быть ноль! Если справа тусуются ещё какие-то члены, то переносим их в левую часть и приводим подобные.
Конечно, если уравнение уже дано в стандартном виде, то первый этап делать не нужно.)
Как только уравнение представлено в стандартном виде, приступаем ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
Если опыта пока что мало, во избежание досадных ошибок бывает очень полезным выписать их отдельно.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Внимание! На данном этапе сразу же извлекаем корень из дискриминанта! Если красиво извлекается, конечно.)
4. Подставляем все значения в общую формулу, считаем корни уравнения и записываем ответ.
Вот и весь алгоритм. Простой и безотказный. Ну что, тренируемся на кошках?
Например, надо решить вот такое уравнение:
Работаем прямо по пунктам.
1. Приводим уравнение к стандартному виду.
Уравнение уже дано нам в стандартном виде. Стало быть, уже готово к решению. Слева — полный набор членов, выстроенных по убыванию степеней, а справа — ноль. Посему переходим сразу ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Аккуратно подставляем наши коэффициенты a, b и с в формулу дискриминанта. Подставляем со своими знаками! Частенько именно в знаках коэффициентов народ и путается. Точнее, не столько в самих знаках, сколько в подстановке отрицательных значений в формулу дискриминанта. Вот и не ленимся, аккуратно пишем все знаки и скобочки. Трудов много не отнимет, зато гарантированно убережёт от досадных промахов:
Извлекаем корень из дискриминанта:
Отлично, корень извлекается чисто. Теперь переходим к последнему, самому главному этапу — считаем наши корни.
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Опять же, аккуратно подставляем все числа в формулу, со всеми знаками и скобочками:
Вот и всё. Это ответ.)
Кстати сказать, если вы просто решаете квадратное уравнение, то нет особой нужды отдельно считать дискриминант. Можно работать напрямую с общей формулой, просто аккуратно подставляя в неё коэффициенты a, b и с.
В нашем случае можно было бы сразу записать:
Но такое оформление чревато тем, что, впопыхах, можно где-нибудь потерять минус. Оно вам надо? Посему лучше считайте дискриминант отдельно — ошибок меньше будет. Естественно, посчитав дискриминант, не забывайте про корень.) Специально акцентирую внимание на этом моменте, потому что сам дискриминант народ обычно считает правильно, а вот корень извлечь частенько забывает… К тому же, привыкнув к отдельному поиску дискриминанта, вы быстрее запомните его общую формулу — в более серьёзных заданиях пригодится. Например, в задачах с параметрами. Такие задачи — высший пилотаж на ЕГЭ!
Естественно, бывают и сюрпризы. Не без этого… И к ним (к сюрпризам) тоже надо быть готовым, да. Чтобы не растеряться, в случае чего…) Рассмотрим первый сюрприз. Самый безобидный.
Например, дано нам такое уравнение:
Как обычно, работаем прямо по алгоритму.
1. Приводим уравнение к стандартному виду.
Уравнение пока не готово к решению. Справа нужен ноль, а у нас справа тусуется 4х. Не беда: переносим 4х влево и выстраиваем члены по убыванию степеней:
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
А вот и первый сюрприз.) Дискриминант не является точным квадратом целого числа! И корень из дискриминанта извлекается плохо:
Что делать? Не решается уравнение? Ну да, как же!
Ничего страшного.) Работаем прямо с корнем. Естественно, если есть возможность, то выносим всё, что извлекается, за знак корня:
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Корни нашего уравнения получились иррациональными. Ну и ничего страшного. Бывает.) Такой уж пример.
Открою небольшой секрет. Обычно задания на квадратные уравнения составляются так, чтобы корень из дискриминанта извлекался ровно и, тем самым, корни в ответе получались красивыми — либо целыми, либо рациональными. И народ постепенно привыкает к таким простым примерам наивно полагая, что дискриминант всегда обязан получаться точным квадратом. Не обязан! Более того, суровая реальность такова, что некрасивый дискриминант (а вместе с ним и лохматые иррациональные корни) — скорее правило, чем исключение! И если вы захотите задать какое-нибудь квадратное уравнение, выбрав в нём коэффициенты a, b и с случайным образом, то с вероятностью 99% корни вашего квадратного уравнения будут числами иррациональными.
Но иррациональных корней вовсе не надо бояться.) Ибо они — точно такие же числа, как и все остальные. Кстати говоря, в более серьёзных заданиях (неравенствах, задачах с параметрами) иррациональные корни встречаются сплошь и рядом. И с ними надо обязательно уметь работать — сравнивать, изображать на числовой оси и т.д. И мы тоже поработаем! В соответствующих уроках.)
Как видите, процедура решения полных квадратных уравнений проблем не вызывает. Всё просто, быстро, не больно.) Главное — аккуратно подставляйте коэффициенты в формулу дискриминанта и общую формулу корней. И считайте себе.) И что, думаете, ошибиться нельзя? Ну да, как же…
Вот краткий перечень глупых ошибок при решении квадратных уравнений:
1. Путаница в знаках. Ошибки в подстановке отрицательных коэффициентов в формулу дискриминанта и в общую формулу корней .
2. Забывают извлечь корень из дискриминанта.
3. При работе с общей формулой корней в знаменатель дроби частенько подставляется не 2а, как положено, а просто двойка. Привыкает, видите ли, народ к простым уравнениям, с первым коэффициентом единичкой (а=1). Внимательнее надо быть, да.)
Например, дано такое уравнение:
Уравнение, в принципе, уже дано нам в стандартном виде. Слева — квадратный трёхчлен, построенный по убыванию степеней, справа — ноль.
Наши коэффициенты будут:
Можно приступать к решению. Только это… коэффициенты — дробные. Неудобно как-то…
Согласен, неудобно! Всё-таки лучше, когда уравнение безо всяких дробей, в линеечку.) Вот и избавимся сначала от дробей. На что надо домножить обе части уравнения, чтобы и двойка сократилась и тройка? На 6! Вот и домножаем. Слева получим:
А что будет справа? Справа будет ноль. Ноль на что ни умножай — всё равно ноль будет. Хорошее число.)
-2х 2 + 9х — 30 = 0
И опять не бросаемся решать, считать дискриминант и прочее. Минус перед иксом в квадрате — нехорош. Забыть его очень легко. Посему избавимся от этого минуса умножением обеих частей на (-1). Проще говоря, поменяем слева все знаки:
2х 2 — 9х + 30 = 0
Ну вот. А теперь — по накатанной колее. Выписываем коэффициенты:
Вот так штука! А дискриминант-то отрицательный! Не можем мы корень из отрицательного числа извлечь. И сами корни посчитать, стало быть, тоже не можем, да. Стало быть, ответ — решений нет.
Это был второй сюрприз. Надеюсь, теперь отрицательный дискриминант в каком-нибудь примере вас нисколько не смутит.)
Это всё что касается полных квадратных уравнений. Теперь переходим к неполным.)
Неполные квадратные уравнения
Неполными, напоминаю, называются квадратные уравнения, где чего-то не хватает — или bx или с. Или обоих членов сразу.
Неполные квадратные уравнение также можно решать через дискриминант, по общей формуле. Надо только правильно догадаться, чему равняются коэффициенты a, b и с.
Догадались? В первом случае a = 1, b = -3, а свободный член с вообще отсутствует! Что это означает? В математике это означает, что с=0! Вот и всё.)
Во втором уравнении всё аналогично, только нулю будет равно не с, а b!
Но неполные уравнения можно решать гораздо проще. Безо всяких дискриминантов и безо всяких формул! Зачем же из пушки по воробьям…
Например, такое уравнение:
Что здесь можно сделать в левой части? Сильнее всего напрашивается вынести икс за скобки и разложить левую часть на множители. Давайте вынесем:
И что дальше? А то, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю! Вот и приравниваем (в уме!) каждый из множителей к нулю и получаем:
И все дела! Это и будут корни нашего уравнения. Оба годятся.) При подстановке каждого из них в исходное уравнение мы получим железное равенство 0=0. Как видите, решение куда проще, чем через дискриминант!
Теперь рассмотрим другое уравнение:
А здесь что можно сделать? Можно -16 перенести вправо:
Остаётся корень извлечь из 16 и — ответ готов:
И так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки и разложения на множители, либо же переносом свободного члена вправо с последующим извлечением корня. Спутать эти два способа — надо очень хорошо постараться.) Ибо в первом случае вам пришлось бы корень из икса извлекать, что как-то не очень, а во втором случае выносить за скобки нечего…
Подытожим тему практическими советами.
1. Перед решением любого квадратного уравнения приводим его к стандартному виду, выстраиваем левую часть по убыванию степеней.
2. Если в уравнении имеются дробные коэффициенты, избавляемся от дробей умножением всего уравнения на нужный множитель.
3. Если коэффициент перед иксом в квадрате отрицательный, избавляемся от минуса умножением всего уравнения на (-1).
Ну что, наш урок окончен. Теперь можно и порешать.)
Видео:Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать
Квадратное уравнение
Загляни сюда, – вдруг узнаешь себя!
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.
Во первых, почему рассматриваются только случаи при 
? Просто потому, что при 
у нас уже будет не квадратное уравнение, а линейное.
Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?
Начнем с того, что иногда происходит путаница с коэффициентами 
, 
и 
. Ни в коем случае мы не считаем, что – это тот коэффициент, что стоит на первом месте! Но – тот, что при 
. Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее , на последнее – свободный от 
член (если таковой имеется). Например, уравнение 
будем переписывать так 
.
Далее, некоторых может сбить с толку минусовой коэффициент при старшем члене (то есть ). В этом случае советую домножать обе части уравнения на -1. Например, встречая уравнение 
, переписывать его в таком виде 
, и только потом высчитывать дискриминант, находить корни.
И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение 
, спешат выносить за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса 
влево примет вид 
, – решаем мы его через дискриминант.
Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.
Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.
У нас в случае неполного уравнения будет всегда получаться либо уравнение с двумя , либо с одним . Что делать, в случае, если у нас оба слагаемых содержат (например, 
)? Ну, конечно, выносить его за скобку (
), в этом случае будем всегда получать, что произведение двух множителей равно 
. Когда такое возможно? Конечно, когда один из множителей равен нулю (либо 
, либо 
). В этом случае у нас всегда один из корней будет нулевым.
Во втором же случае, неполное уравнение будет содержать лишь одно слагаемое с (например, 
или 
). Если свободный член отрицательный (как в первом случае, 
), то мы всегда сможем разложить левую часть на множители по формуле разность квадратов ( для уравнения имеем 
, далее 
). Если же свободный член положителен, то уравнение не имеет корней (действительно, в уравнении первое слагаемое должно бы быть равным -3, чтобы в сумме с 3 дать 0, но такое невозможно).
В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.
Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если 
0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»54″ style=»vertical-align: 0px;»/>, то будем иметь два корня, если 
, то имеем один корень (или два совпавших), наконец, если 
, то корней нет.
🔥 Видео
Как решать уравнения с дробью? #shortsСкачать
Сложные уравнения. Как решить сложное уравнение?Скачать
Как решают уравнения в России и СШАСкачать
Математика 5 класс. Умножение, деление, сокращение обыкновенных дробейСкачать
Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Задание №1 "Упростить выражение" по теме "Умножение и сложение многочленов и одночленов". Алгебра 7Скачать
Решение матричных уравненийСкачать
КАК РЕШАТЬ ПРОПОРЦИИ?Скачать
РЕШЕНИЕ УРАВНЕНИЙ ЛЕГКО ! 1 КЛАСС МАТЕМАТИКА УРАВНЕНИЯ - ПЕТЕРСОН / ОБЪЯСНЕНИЕ КАК РЕШАТЬ УРАВНЕНИЯСкачать
Произведение одночлена и многочлена. Умножение одночлена и многочлена. 7 класс.Скачать
Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать
Решить уравнение с дробями - Математика - 6 классСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Умножение одночлена на многочлен. Алгебра, 7 классСкачать
Решение уравнений, 6 классСкачать
Умножение, деление и сложение дробей #математика #алгебра #дроби #5классСкачать
как решать дробиСкачать
