Можно ли делить уравнение на косинус

Методы решения тригонометрических уравнений.

1. Алгебраический метод.

( метод замены переменной и подстановки ).

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Урок «Однородные тригонометрические уравнения»

Краткое описание документа:

С помощью этого видеоурока учащиеся смогут изучить тему однородных тригонометрических уравнений.

1) однородное тригонометрическое уравнение первой степени выглядит как a sin x + b cos x = 0;

2) однородное тригонометрическое уравнение второй степени выглядит как a sin 2 x + b sin x cos x + c cos 2 x = 0.

Рассмотрим уравнение a sin x + b cos x = 0. Если а будет равно нулю, то уравнение будет выглядеть как b cos x = 0; если b равно нулю, то уравнение будет выглядеть как a sin x = 0. Это уравнения, которые мы называли простейшими и решали ранее в предыдущих темах.

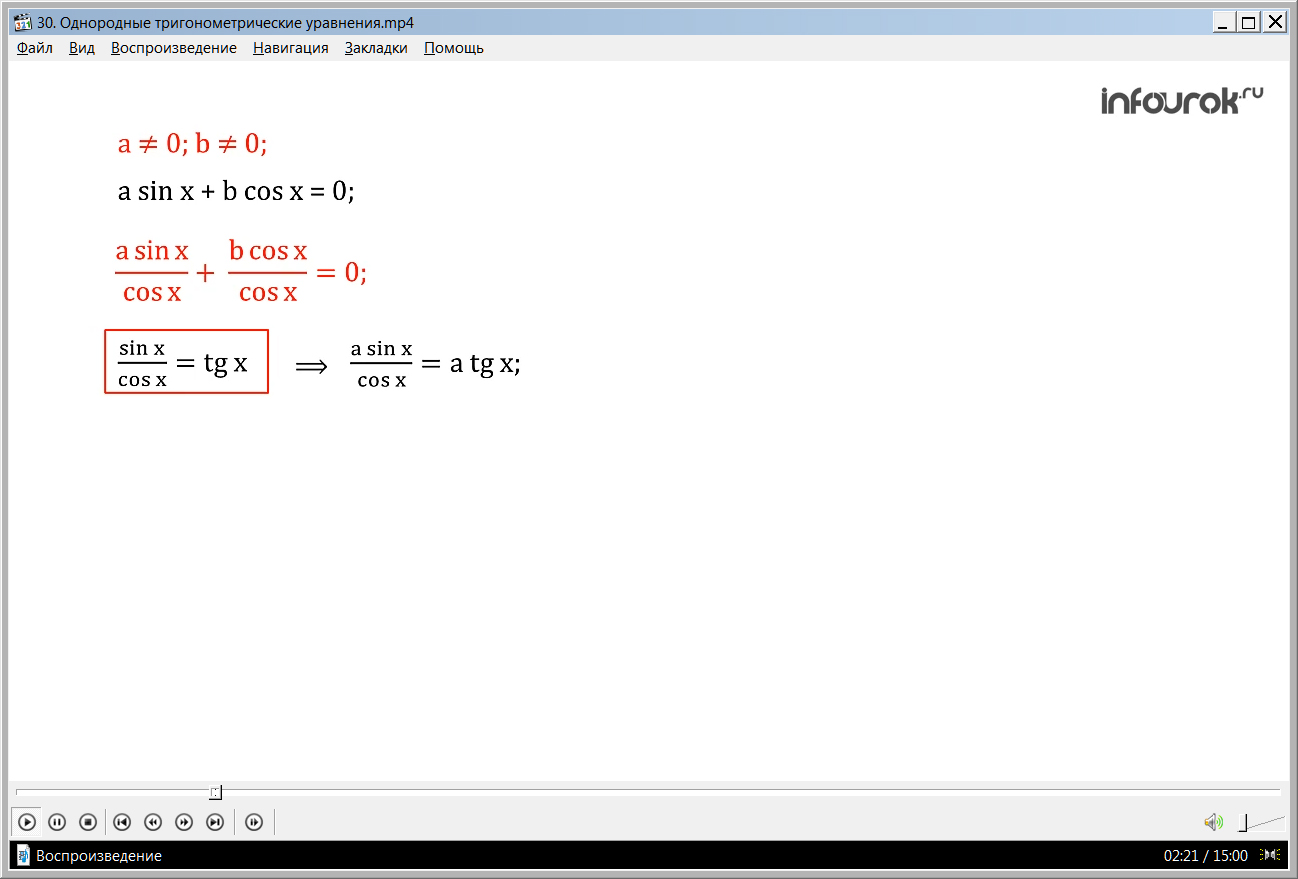
Сейчас рассмотрим вариант, когда a и b не равны нулю. С помощью деления частей уравнения на косинус x и осуществим преобразование. Получим a tg x + b = 0, тогда tg x будет равен – b/а.

Из вышеизложенного следует вывод, что уравнение a sin mx + b cos mx = 0 является однородным тригонометрическим уравнением I степени. Чтобы решить уравнение, его части делят на cos mx.

Разберем пример 1. Решить 7 sin (x/2) – 5 cos (x/2) = 0. Сначала части уравнения делим на косинус(x/2). Зная, что синус, деленный на косинус, это тангенс, получим 7 tg (x/2) – 5 = 0. Преобразовывая выражение, найдем, что значение тангенса (x/2)равно 5/7. Решение данного уравнения имеет вид х = arctg a + πn, в нашем случае х = 2 arctg (5/7) + 2πn.

Рассмотрим уравнение a sin 2 x + b sin x cos x + c cos 2 x = 0:

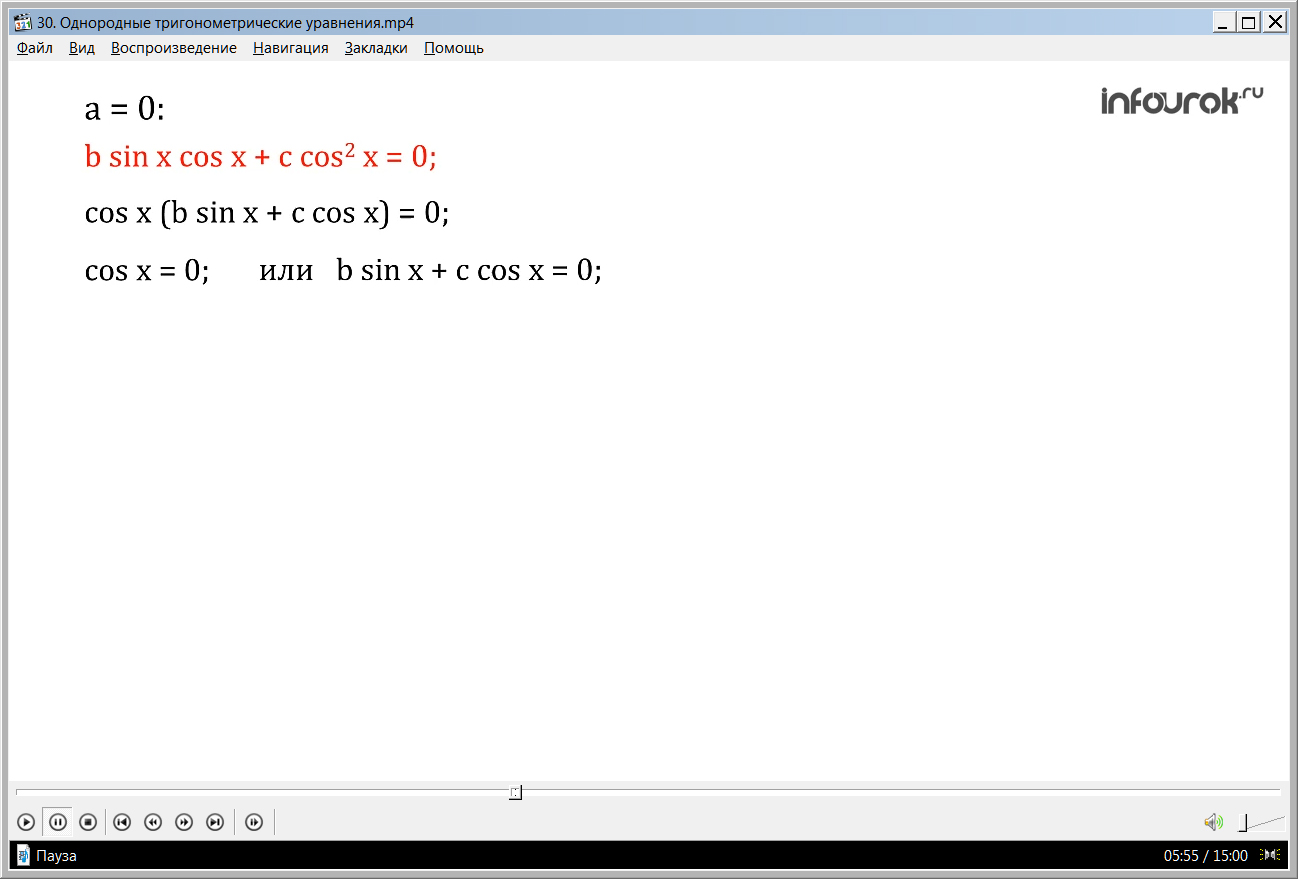
1) при а равном нулю уравнение будет выглядеть как b sin x cos x + c cos 2 x = 0. Преобразуя, получим выражение cos x (b sin x + c cos x) = 0 и перейдем к решению двух уравнений. После деления частей уравнения на косинус x, получим b tg x + c = 0, а значит tg x = – c/b. Зная, что х = arctg a + πn, то решением в данном случае будет х = arctg (– с/b) + πn.

2) если а не равно нулю, то, путем деления частей уравнения на косинус в квадрате, получим уравнение, содержащее тангенс, которое будет квадратным. Это уравнение можно решить путем ввода новой переменной.

3) при с равном нулю уравнение примет вид a sin 2 x + b sin x cos x = 0. Это уравнение можно решить, если вынести синус x за скобку.

Далее автор акцентирует внимание на том, что при решении уравнения a sin 2 x + b sin x cos x + c cos 2 x = 0 можно использовать следующие шаги:

1. посмотреть, есть ли в уравнении a sin 2 x;

2. если в уравнении член a sin 2 x содержится, то решить уравнение можно путем деления обеих частей на косинус в квадрате и последующим введением новой переменной.

3. если в уравнении a sin 2 x не содержится, то решить уравнение можно с помощью выноса за скобки cosx.

Рассмотрим пример 2. Вынесем за скобки косинус и получим два уравнения. Корень первого уравнения x = π/2 + πn. Для решения второго уравнения разделим части этого уравнения на косинус x, путем преобразований получим х = π/3 + πn. Ответ: x = π/2 + πn и х = π/3 + πn.

Решим пример 3, уравнение вида 3 sin 2 2x – 2 sin 2x cos 2x + 3 cos 2 2x = 2 и найдем его корни, которые принадлежат отрезку от – π до π. Т.к. это уравнение неоднородное, необходимо привести его к однородному виду. Используя формулу sin 2 x + cos 2 x = 1, получим уравнение sin 2 2x – 2 sin 2x cos 2x + cos 2 2x = 0. Разделив все части уравнения на cos 2 x, получим tg 2 2x + 2tg 2x + 1 = 0. Используя ввод новой переменной z = tg 2x, решим уравнение, корнем которого будет z = 1. Тогда tg 2x = 1, откуда следует, что x = π/8 + (πn)/2. Т.к. по условию задачи нужно найти корни, которые принадлежат отрезку от – π до π, решение будет иметь вид – π 2 x+b sin x cosx +с cos 2 x= 0 (а синус квадрат икс плюс бэ синус икс косинус икс плюс сэ косинус квадрат икс равно нулю) называют однородным тригонометрическим уравнением второй степени.

Данные уравнения являются элементарными тригонометрическими, и их решение мы рассматривали на прошлых наших темах

Рассмотрим тот случай, когда оба коэффициента не равны нулю. Разделим обе части уравнения а sinx+bcosx = 0 почленно на cosx.

Это мы можем сделать, так как косинус икс отличен от нуля. Ведь, если cosx = 0, то уравнение а sinx+bcosx = 0 примет вид а sinx = 0, а ≠ 0, следовательно sinx = 0. Что невозможно, ведь по основному тригонометрическому тождеству sin 2 x+ cos 2 x=1.

1. Так как = tg x, то = а tg x

Таким образом получим следующее выражение а tg x + b =0.

1.перенесем b в правую часть выражения с противоположным знаком

2. Избавимся от множителя а разделив обе части уравнения на а

Вывод: Уравнение вида а sin mx+bcosmx = 0 (а синус эм икс плюс бэ косинус эм икс равно нулю) тоже называют однородным тригонометрическим уравнением первой степени. Чтобы решить его, делят обе части на cosmx.

ПРИМЕР 1. Решить уравнение 7 sin — 5 cos = 0 (семь синус икс на два минус пять косинус икс на два равно нулю)

Решение. Разделим обе части уравнения почленно на cos, получим

1. = 7 tg (так как соотношение синуса к косинусу – это тангенс, то семь синус икс на два деленное на косинус икс на два, равно 7 тангенс икс на два)

2. -5 = -5 (при сокращении cos )

Таки образом получили уравнение

7tg — 5 = 0, Преобразуем выражение, перенесем минус пять в правую часть, изменив знак.

Мы привели уравнение к виду tg t = a, где t=, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg a + πn, то решение нашего уравнения будет иметь вид:

= arctg + πn, найдем х

Ответ: х=2 arctg + 2πn.

Перейдем к однородному тригонометрическому уравнению второй степени

Рассмотрим несколько случаев.

b sin x +сcos x= 0.А эти уравнения мы уже умеем решать.

Разделим обе части уравнения почленно на cosх, получим

1 (так как соотношение синуса к косинусу – это тангенс).

Таким образом получаем уравнение: btg х+с=0

Мы привели уравнение к виду tg t = a, где t= х, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg a + πn, то решение нашего уравнения будет:

II. Если а≠0, то обе части уравнения почленно разделим на cos 2 x.

(Рассуждая аналогично, как и в случае с однородным тригонометрическим уравнением первой степени, косинус икс не может обратится в ноль).

III. Если с=0, то уравнение примет вид а sin 2 x+bsinxcosx= 0. Это уравнение решается методом разложения на множители (вынесем sinxза скобку).

ПРИМЕР 2. Решить уравнение sinxcosx — cos 2 x= 0 (синус икс, умноженный на косинус икс минус корень из трех, умноженный на косинус квадрат икс равно нулю).

Решение. Разложим на множители (вынесем за скобку cosx). Получим

cos x(sin x — cos x)= 0, т.е. cos x=0 илиsin x — cos x= 0.

Ответ: х =+ πn, х= + πn.

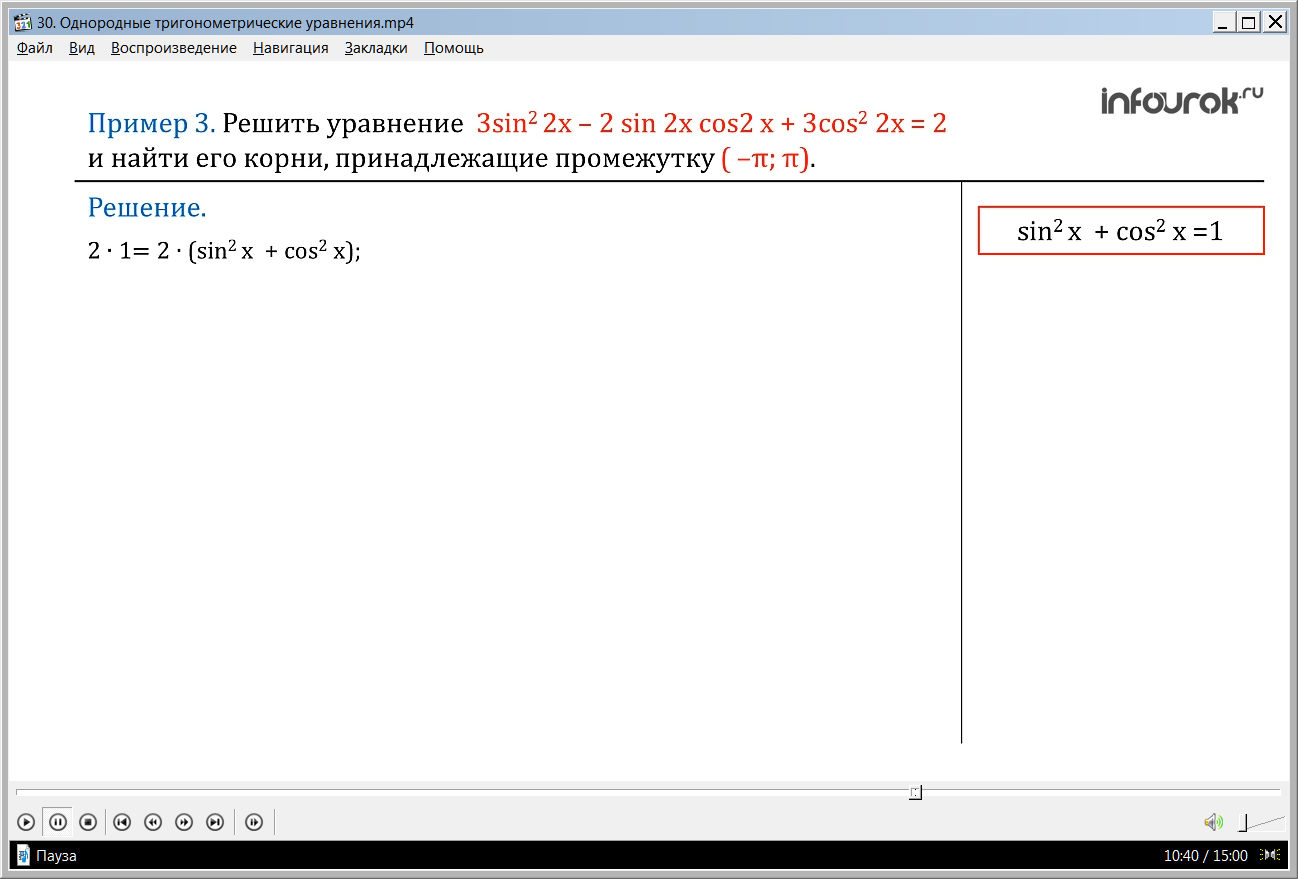
ПРИМЕР 3. Решить уравнение 3sin 2 2x — 2 sin2xcos2 x +3cos 2 2x= 2 (три синус квадрат двух икс минус удвоенное произведение синуса двух икс на косинус двух икс плюс три косинус квадрат двух икс) и найти его корни, принадлежащие промежутку ( — π; π).

Решение. Это уравнение не однородное, поэтому проведем преобразования. Число 2, содержащееся в правой части уравнения, заменим произведением 2·1

Так как по основному тригонометрическому тождеству sin 2 x + cos 2 x =1, то

2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) = раскрыв скобки получим: 2 sin 2 x + 2 cos 2 x.

2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) =2 sin 2 x + 2 cos 2 x

Значит уравнение 3sin 2 2x — 2 sin2xcos2 x +3cos 2 2x= 2 примет вид:

3sin 2 2x — 2 sin 2x cos2 x +3cos 2 2x = 2 sin 2 x + 2 cos 2 x.

Далее все перенесем в левую часть и приведем подобные слагаемые:

3sin 2 2x — 2 sin 2x cos2 x +3cos 2 2x — 2 sin 2 x — 2 cos 2 x=0,

sin 2 2x — 2 sin 2x cos2 x +cos 2 2x =0.

Получили однородное тригонометрическое уравнение второй степени. Применим способ почленного деления на cos 2 2x :

tg 2 2x – 2tg 2x + 1 = 0.

Введем новую переменную z= tg2х.

Имеем z 2 — 2 z + 1 = 0. Это квадратное уравнение. Заметив в левой части формулу сокращенного умножения — квадрат разности ( ), получим (z – 1) 2 = 0, т.е. z = 1. Вернемся к обратной замене:

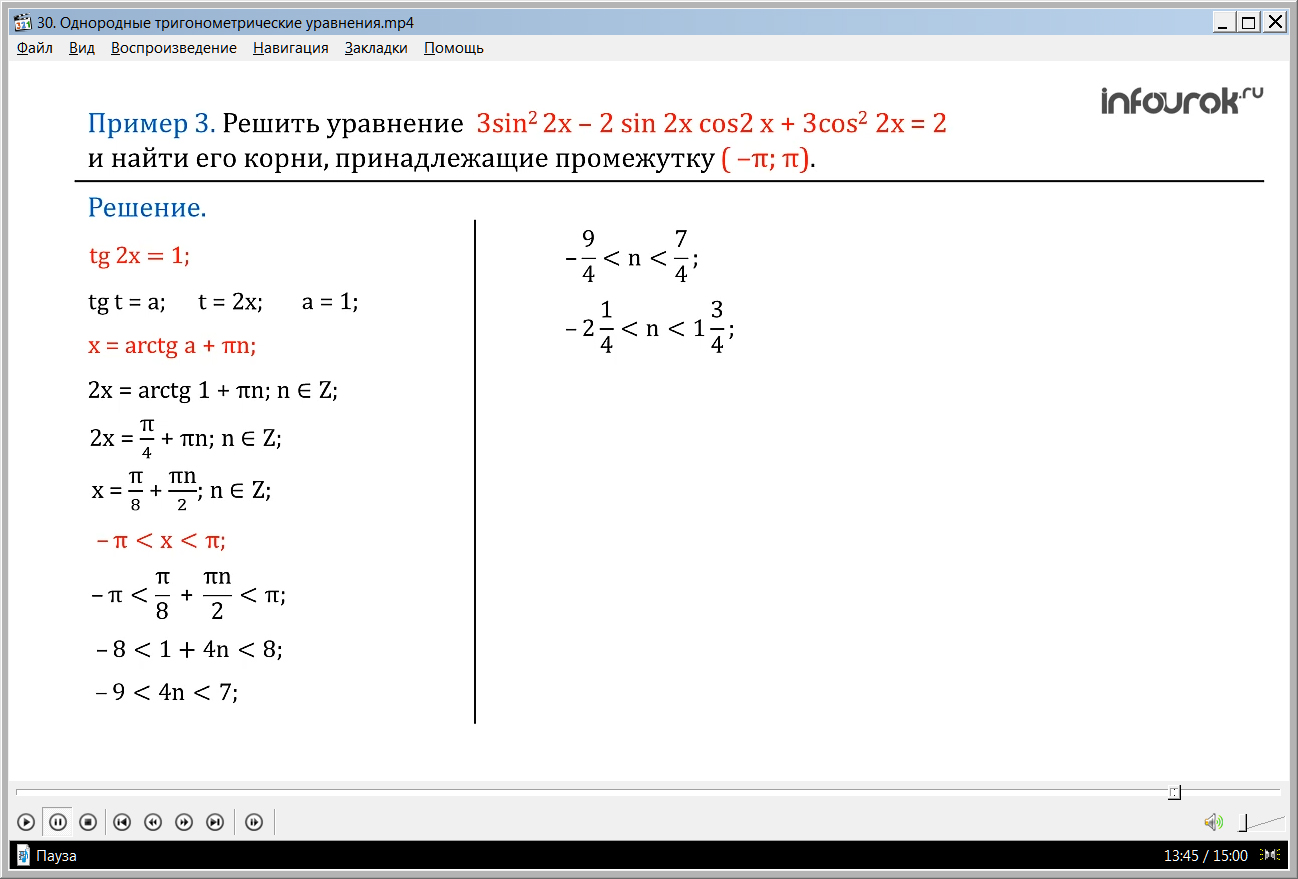
Мы привели уравнение к виду tg t = a, где t= 2х, a =1 . А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg x a + πn, то решение нашего уравнения будет:

х= + , ( икс равно сумме пи на восемь и пи эн на два).

Нам осталось найти такие значения х, которые содержатся в интервале

( — π; π), т.е. удовлетворяют двойному неравенству — π х π. Так как

х= + , то — π + π. Разделим все части этого неравенства на π и умножим на 8, получим

перенесем единицу в право и в лево, поменяв знак на минус один

разделим на четыре получим,

для удобства в дробях выделим целые части

– —> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

27.07.2014

Алгебра

Видеоурок

8867

858

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Тригонометрические уравнения. Как решать тригонометрические уравнения?

Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.

Если проще: это уравнения, в которых неизвестные (иксы) или выражения с ними находятся внутри синусов , косинусов , тангенсов и котангенсов .

Как решать тригонометрические уравнения:

Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:

где (t) – выражение с иксом, (a) – число. Такие тригонометрические уравнения называются простейшими. Их легко решать с помощью числовой окружности ( тригонометрического круга ) или специальных формул:

(sin ⁡x=a) (⇔) ( left[ beginx=arcsin a+2πn, n∈Z\ x=π-arcsin a+2πl, l∈Zendright.)
если (a∈[-1;1])

Инфографику о решении простейших тригонометрических уравнений смотри здесь: (sinx=a) , (cosx=a) , (tgx=a) и (ctgx=a) .

Пример. Решите тригонометрическое уравнение (sin⁡x=-)(frac).
Решение:

Решим уравнение с помощью числовой окружности. Для этого:
1) Построим оси.
2) Построим окружность.
3) На оси синусов (оси (y)) отметим точку (-) (frac) .
4) Проведем перпендикуляр к оси синусов через эту точку.
5) Отметим точки пересечения перпендикуляра и окружности.
6)Подпишем значения этих точек: (-) (frac) ,(-) (frac) .
7) Запишем все значения соответствующие этим точкам с помощью формулы (x=t+2πk), (k∈Z):
(x=-) (frac) (+2πk), (k∈Z); (x=-) (frac) (+2πn), (n∈Z)

Что означает каждый символ в формуле корней тригонометрических уравнений смотри в видео .

Внимание! Уравнения (sin⁡x=a) и (cos⁡x=a) не имеют решений, если (a ϵ (-∞;-1)∪(1;∞)). Потому что синус и косинус при любых икс больше или равны (-1) и меньше или равны (1):

Пример. Решить уравнение (cos⁡x=-1,1).
Решение: (-1,1 (frac) , (frac)
7) Запишем все значения этих точек. Так как они находятся друг от друга на расстоянии ровно в (π), то все значения можно записать одной формулой:

Ответ: (x=) (frac) (+πk), (k∈Z).

Пример. Решите тригонометрическое уравнение (cos⁡(3x+frac)=0).
Решение:

Опять воспользуемся числовой окружностью.
1) Построим окружность, оси (x) и (y).
2) На оси косинусов (ось (x)) отметим (0).
3) Проведем перпендикуляр к оси косинусов через эту точку.
4) Отметим точки пересечения перпендикуляра и окружности.
5) Подпишем значения этих точек: (-) (frac),(frac) .
6)Выпишем все значение этих точек и приравняем их к аргументу косинуса (к тому что внутри косинуса).

7) Дальше решать в таком виде несколько трудновато, разобьем уравнение на два.

8) Как обычно в уравнениях будем выражать (x).
Не забывайте относиться к числам с (π), так же к (1), (2), (frac) и т.п. Это такие же числа, как и все остальные. Никакой числовой дискриминации!

Ответ: (x=) (frac) (+) (frac) (x=-) (frac) (+) (frac) , (k∈Z).

Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы , и особые методы решений уравнений:
— Метод введения новой переменной (самый популярный в ЕГЭ).
— Метод разложения на множители .
— Метод вспомогательных аргументов.

Рассмотрим пример решения квадратно-тригонометрического уравнения

Пример. Решите тригонометрическое уравнение (2cos^2⁡x-5cos⁡x+2=0)
Решение:

Сделаем замену (t=cos⁡x).

Наше уравнение превратилось в типичное квадратное . Можно его решить с помощью дискриминанта .

(D=25-4 cdot 2 cdot 2=25-16=9)

Делаем обратную замену.

Первое уравнение решаем с помощью числовой окружности.
Второе уравнение не имеет решений т.к. (cos⁡x∈[-1;1]) и двум быть равен не может ни при каких иксах.

Запишем все числа, лежащие на числовой окружности в этих точках.

Ответ: (x=±) (frac) (+2πk), (k∈Z).

Пример решения тригонометрического уравнения с исследованием ОДЗ:

Пример(ЕГЭ). Решите тригонометрическое уравнение (frac<2cos^2⁡x-sin>) (=0)

Есть дробь и есть котангенс – значит надо записать ОДЗ . Напомню, что котангенс это фактически дробь:

Потому ОДЗ для ctg(x): (sin⁡x≠0).

Отметим «нерешения» на числовой окружности.

🎥 Видео