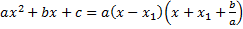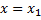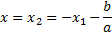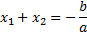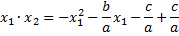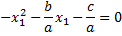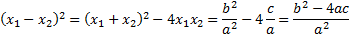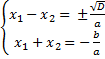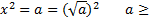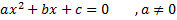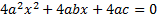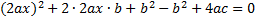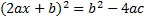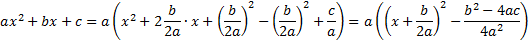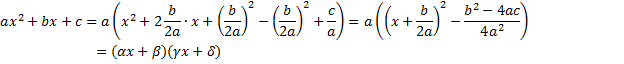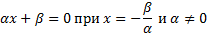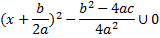Может ли квадратное уравнение иметь три корня (3 видео)

Летняя школа для учителей математики. Преподавание квадратного трехчлена

Содержание

Квадратный трехчлен в школе
Теорема Виета
Теорема о корнях квадратного уравнения
Теорема о разложении квадратного трехчлена на множители.
Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом
Квадратное уравнение. Дискриминант. Теорема Виета.
теория по математике 📈 уравнения
Дискриминант
Теорема Виета
💡 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратный трехчлен в школе

Традиционно тема включает четыре теоремы:

О корнях квадратного уравнения (краеугольный камень всей теории квадратного уравнения).
О разложении квадратного трехчлена на (линейные) множители.
Виета.
Обратную Виета.

Чаще всего, в школе учеников знакомят с доказательствами этих теорем в общих чертах, связывая одну с другой. Например, теорема Виета объясняется на основе теоремы о корнях квадратного уравнения.

Не столь стандартный подход: рассмотреть все четыре теоремы независимо друг от друга. Эта практика пригодится ученикам, изучающим математику на углубленном уровне.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Теорема Виета

Может ли квадратное уравнение иметь два одинаковых корня? Нет: уравнение может иметь либо ноль корней, либо один, либо два. У трехчлена вполне могут быть два одинаковых корня — это известно из общей теории многочленов. Часто говорят, что всякий многочлен в n-ной степени имеет n корней — а на самом деле: n корней с учетом кратности.

Как сформулировать теорему Виета, чтобы она не зависела от теоремы о корнях? Если квадратный трехчлен имеет хотя бы один корень, то он обязательно имеет и еще один корень, возможно совпадающий с первым, и при этом их сумма равна (тому-то) и произведение равно.

Докажем, что x₁ обязательно имеет еще один корень — такой, что сумма корней равняется 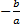, а произведение .

Данное выражение обнуляется при:

Мы доказали это, не используя формулу корней. Теперь перемножим:

Все это выражение ровно в -a раз меньше, чем 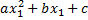. То есть

Тогда произведение корней равняется .

Обычно школьников учат, что нельзя применять теорему Виета, не проверив, что корни есть. Данное доказательство позволяет говорить: «Применяйте теорему Виета, убедившись, что трехчлен имеет хотя бы один корень».

Как из теоремы Виета вывести теорему о корнях квадратного уравнения?

Рассмотрим вспомогательное утверждение.

Получается, что если есть корни, то квадрат их разности равен дискриминанту, деленному на а 2 . То есть если корни есть, то дискриминант больше либо равен нулю, и, если дискриминант отрицательный, то корней быть не может.

Так мы выводим формулу корней, рассуждая в обратную сторону — чтобы глубже ориентироваться в материале.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Теорема о корнях квадратного уравнения

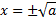
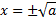
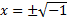
x 2 = a. Почему нельзя сказать ? Ответ на задание «при каждом а решить уравнение» должен иметь смысл при каждом а, поэтому выражение не может быть ответом. Ответ в задаче с параметром не может не иметь смысл ни в одной точке в значении а, которая входит в данную область. Кроме того, допустим, а=-1. Разве можно записать x 2 =-1 и ответ ?

x 2 = a — нельзя единообразно решить для всех а.

Рассмотрим необычный способ решения уравнения

Решим методом деления полного квадрата. Умножим на 4а, чтобы гарантированно выделился полный квадрат.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Теорема о разложении квадратного трехчлена на множители.

Данная теорема идет рука об руку с теоремой о корнях.

Если дискриминант отрицательный, как доказать, что нет разложения на линейные множители? Рассмотрим от противного: допустим, дискриминант отрицательный.

Пусть такое разложение существует. Это значит, что при всех значениях x данные выражения действительно равны. Альфа или гамма: хотя бы один из этих коэффициентов не равен нулю.

Таким образом, наш квадратный трехчлен при отрицательном дискриминанте не разлагается на линейные множители.

Видео:Квадратное уравнение с параметром. Исследование корней квадратного уравнения. Алгебра 8 классСкачать

Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом

Разделы: Математика

Устный счет:

1. При каком значении Х , выражение принимает минимальное значение

а) ; б)
2. Зависимость y(x) выражается формулой y = 13x + 1 выразить x(y)

3. Не решая уравнения, определить, равносильны ли они:

4. Выделить полный квадрат:

5. Вычислить пары чисел , удовлетворяющих условиям

а) m + n = 4
mn = 4

б) m + n = –3
mn = –18

Какое уравнение называется полным?
Что такое корни квадратного уравнения?
Сколько корней может иметь квадратное уравнение?

Теорема. Квадратное уравнение не может иметь более двух различных корней.

Доказательство:

Предположим, что уравнение три различных корня:

Если уравнение имеет корень, то после подстановки его в уравнение получится верное числовое равенство:

(1)
(2)
(3)

из (2) отнимаем (1)

–

_____________________

В каком случае произведение равно 0?

Так как = > 0 = > a+ b = 0. (4)

–

_________________

= > a+ b = 0 (5)

–

________________

а0 = > = > ,
а по условию пришли к противоречию.

Давайте решим уравнение:

Самостоятельно:

Вместе:

б)

Нравится ли этот способ? Нет! Тогда будем рассуждать иначе:

(формулу для нахождения корней квадратного уравнения учить проговаривать словами).

– дискриминант квадратного уравнения.

По теореме, доказанной нами , уравнение не может иметь более двух корней.

Количество корней зависит от D.

1). D > 0
2). D = 0

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Видео:Составьте квадратное уравнение, корнями которого являются числаСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить