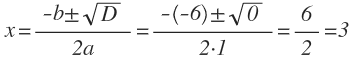Может ли квадратное уравнение иметь дискриминант 23 (2 видео)

math4school.ru

Содержание

Квадратный трёхчлен
Немного теории
Задачи с решениями
Задачи без решений
Может ли квадратное уравнение ах^2+bx+c=0 c ЦЕЛЫМИ коэффициентами иметь дискриминант, равный 23?
Как найти дискриминант квадратного уравнения
Понятие квадратного уравнения
Понятие дискриминанта
Как решать квадратные уравнения через дискриминант
Примеры решения квадратных уравнений с помощью дискриминанта
📺 Видео

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Квадратный трёхчлен

Немного теории

В большинстве задач, сводящихся к исследованию квадратичной функции

полезно представить себе её график:

если он пересекает ось Ох в двух точках (корнях) х₁ и х₂, то между корнями значения функции у = f(х) противоположны по знаку числу а, а вне отрезка [х₁; х₂] – совпадают по знаку с числом а;
при этом вершина параболы у = f(х) (абсцисса которой равна полусумме корней) соответствует точке экстремума функции у = f(х): минимума, если а > 0, и максимума, если а

В ряде задач полезно использовать такой факт:

если непрерывная на отрезке [а, b] функция у = f(х) принимает в концах этого отрезка значения разных знаков, то между точками a и b лежит хотя бы один корень уравнения f(х) = 0.

Задачи с решениями

1. Известно, что a + b + c 2 + bx + c = 0 не имеет действительных корней. Определить знак коэффициента с.

Квадратный трёхчлен f(x) = ax 2 + bx + c не имеет действительных корней, значит, он сохраняет один и тот же знак для всех значений аргумента х. Так как f(1) = a + b + c

2. Может ли квадратное уравнение ax 2 + bx + c = 0 с целыми коэффициентами иметь дискриминант равный 23?

Допустим, что дискриминант указанного уравнения равен числу 23. Тогда можно записать:

Заметим, что b – 5 и b + 5 – числа одинаковой чётности, поэтому их произведение, если оно чётно, делится на 4. Правая часть последнего равенства есть чётное число, не делящееся на 4. Полученно противоречие, значит, сделаное допущение ложно.

3. Найти все пары действительных чисел p, q, для которых многочлен x 4 + px 2 + q, имеет 4 действительных корня, образующих арифметическую прогрессию.

Многочлен x 4 + px 2 + q, имеет 4 действительных корня в том и только в том случае, если многочлен у 2 + pу + q (относительно у = x 2 ) имеет два неотрицательных корня, т.е. числа р и q удовлетворяют условиям

Если исходный многочлен имеет 4 действительных корня (а именно: –х₁, –х₂, х₁, х₂, где без ограничения общности считаем, что х₁ > х₂ > 0), то они образуют арифметическую прогрессию тогда и только тогда, когда совместна система

(смотрите теорему Виета и обратную к ней), т.е. когда q = 0,09 · р 2 . Таким образом, все искомые пары чисел р, q описываются условиями

(неравенства p 2 > 4q и q > 0,вытекают из последнего равенства).

4. Пусть a, b, c – действительные числа. Доказать, что уравнение

всегда имеет хотя бы один действительный корень. Выяснить, когда таких корня два.

Без ограничения общности рассуждений можно считать, что a b c. Рассмотрим все возможные случаи:

f ( a ) = ( a – b ) ( a – c ) > 0,

f ( c ) = ( c – a ) ( c – b ) > 0.

Так как f ( x ) – непрерывная квадратичная функция, принимающая значения разного знака на концах интервалов (a; b) и (b; c), то она имеет два различных действительных корня х 1 и х 2 . Более того

Решение задачи окончено.

5. Дан многочлен ax 2 + bx + c. За один ход разрешается заменить х на (х – k) или заменить многочлен целиком на многочлен

Можно ли после нескольких ходов из многочлена x 2 – 3x – 4 получить многочлен x 2 – 2x – 5?

Нетрудно убедиться, что при указанных заменах исходного многочлена его дискриминант не изменяется. Значит, если из многочлена x 2 – 3x – 4 можно получить многочлен x 2 – 2x – 5, то их дискриминанты должны быть равны. Однако это не так.

6. Найдите все значения a и b, такие, что для любого х из отрезка [–1; 1] будет выполняться неравенство

Пусть числа а и b такие, что для любого х из отрезка [–1; 1] выполняется данное неравенство, т. е,

Полагая здесь последовательно х = 0, х = 1, х = – 1, получаем, что а и b удовлетворяют следующей системе неравенств:

Сложив почленно два последних неравенства, подучим

Отсюда и из первого неравенства следует, что b = –1. Тогда а удовлетворяет следующим двум неравенствам:

и поэтому, а = 0. Таким образом, если существуют числа а и b, удовлетворяющие условию задачи, то

и других решений задача не имеет.

Чтобы доказать, что найденные значения а = 0, b = – 1 являются решением задачи, остается проверить, что для любого х из отрезка [–1; 1] верно двойное неравенство

А оно равносильно неравенству

которое, очевидно, справедливо на числовом промежутке [–1; 1].

7. По трём прямолинейным дорогам с постоянными скоростями идут три пешехода. В начальный момент времени они не находились на одной прямой. Докажите, что они могут оказаться на одной прямой не более двух раз.

Поставим каждому из пешеходов в соответствие точку в прямоугольной системе координат. Точки (х₁; у₁), (х₂; у₂), (х₃; у₃) лежат на одной прямой тогда и только тогда, когда

Так как скорости пешеходов постоянны, то х₁(t), у₁(t), х₂ (t), у₂(t), х₃(t) и у₃(t) – линейные функции от времени t и последнее равенство является квадратным уравнением относительно t, которое может иметь не более двух решений t₁ и t₂. Это и есть те два возможных момента времени, когда все три пешехода могут оказаться на одной прямой.

8. На координатной плоскости Oхy нарисован график функции y = x 2 . Потом оси координат стёрли, осталась только парабола. Как при помощи циркуля и линейки восстановить оси координат и единицу длины?

Докажем следующую лемму.

Лемма. Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы.

Доказательство. Пусть хорды AB и CD параболы лежат на параллельных прямых

тогда абсциссы точек A , B , C , D – это корни уравнений

а абсциссы точек M и N – полусуммы корней этих уравнений, то есть по теореме Виета равны k /2. Следовательно, точки M и N лежат на прямой х = k /2, которая параллельна оси Oy . Лемма доказана.

Вернёмся к исходной задаче.

Последовательно осуществляем следующие построения:

1) две параллельные прямые, каждая из которых пересекает параболу в двух точках;

2) прямую через середины получающихся отрезков;

3) перпендикуляр к этой прямой, пересекающий параболу в двух точках А и В;

4) серединный перпендикуляр к отрезку АВ – это ось Оу;

5) ось Ох перпендикулярна Оу в точке пересечения с параболой;

6) единичный отрезок – абсцисса пересечения прямой у = х с параболой.

9. Учитель написал на доске квадратный трехчлен х 2 + 10х + 20, после чего по очереди каждый из учеников увеличил или уменьшил на единицу либо коэффициент при х, либо свободный член, но не оба сразу. В результате на доске оказался написан квадратный трехчлен х 2 + 20х+10. Верно ли, что в некоторый момент на доске был написан квадратный трехчлен с целыми корнями?

Заметим, что при каждом изменении трехчлена его значение в точке х = – 1 изменяется на 1 (в ту или другую сторону). Значение первого трехчлена

в этой точке равно f(–1) = 11, а последнего,

— g(–1) = –9. Поэтому в какой-то промежуточный момент на доске был написан трехчлен

для которого h(–1)=0. Оба его корня – целые числа: один равен –1, другой по теореме Виета равен –q.

Каждому квадратному трёхчлену

поставим в соответствие точку координатной плоскости Оbc, где вдоль оси Оb будем откладывать значения второго коэффициента, а вдоль Ос – свободного члена. Многочленам

будут соответствовать точки

соответственно. Предложенные в условии операции предполагают перемещение от точки А к точке В вдоль узлов некоторой ломаной L. Узлы L – некоторые целочисленные точки плоскости Оbc, а длина каждого звена L равна 1 (соседние звенья могут лежать на одной прямой).

Так как точки А и В расположены в разных полуплоскостях относительно прямой

то ломаная L одним из своих узлов имеет точку этой прямой. Значит, одним из промежуточных многочленов будет многочлен вида

10. Какова вероятность того, что корни квадратного уравнения x 2 + 2bx + c = 0 действительны?

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b; c) равномерно распределена на квадрате с центром в начале координат и стороной 2B. Решим задачу при фиксированном значении B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

На рисунке более тёмная выделенная область отвечает случаю действительных корней,

более светлая – комплексных.

Для того чтобы уравнение имело действительные корни, необходимо и достаточно, чтобы

На приведенном рисунке изображена парабола с = b 2 и показана область, где наше уравнение имеет действительные корни для B = 4.

Нетрудно подсчитать, что площадь «комплексной» области равна (4 · B 3/2 )/3 (при B > 1), а площадь всего квадрата, конечно, равна 4B 2 . Следовательно, вероятность того, что корни комплексные, равна 1/(3 √ В ). При B = 4 она составляет 1/6. Действительно,

(4 · B 3/2 ) / 3	=	1	=	1
4 B 2	=	3 · √ В	=	3 · √ 4

С ростом B значение дроби 1/ √ В стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Замечание. Рассмотренная задача отличается от такой же задачи, связанной с уравнением

Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

Задачи без решений

1. Корни уравнения х 2 + pх + q = 0, у которого p + q = 198, являются целыми числами. Найдите эти корни.

2. В квадратном уравнении х 2 + pх + q = 0 коэффициенты p и q независимо пробегают все значения от –1 до +1 включительно. Найти множество значений, которые при этом могут принимать действительные корни данного уравнения.

3. Квадратный трёхчлен f ( х ) = ax 2 + bx + c таков, что уравнение f ( х ) = x не имеет действительных корней. Докажите, что уравнение f ( f ( х )) = х так же не имеет вещественных корней.

4. Найдите уравнение общей касательной к параболам у = x 2 + 4x + 8 и у = x 2 + 8x + 4.

Видео:КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

Может ли квадратное уравнение ах^2+bx+c=0 c ЦЕЛЫМИ коэффициентами иметь дискриминант, равный 23?

это равносильно вопросу — имеет ли решение диофантово уравнение
b^2-23=4ac
?

переписав его в форме
b^2-4ac=23
видим, что b может быть только нечётным
введём замену (2n-1)^2=b^2
и подставим её в исходное
2n^2+2n-11=2ac
2n^2+2n-2ac=11
сумма чётных чисел не может быть нечётным, следовательно решений нет

Видео:6. Квадратное уравнение. Дискриминант равен нулю.Скачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Как решать квадратные уравнения через дискриминант. Простое объяснениеСкачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.