Дата добавления: 2015-08-14 ; просмотров: 5103 ; Нарушение авторских прав
| Задание №1 | Задание №2 | Задание №3 |
| Вариант 1 | ||
| Вариант 2 |
Дополнительные задачи
1. Найдите максимум функции: 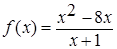
2. Найдите значения функции в точках максимума 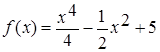
3. Найдите длину промежутка возрастания: у = — х (х-3) 2 3 балла
4. Найдите длину конечного промежутка возрастания: 3 балла
Приложение 4а
| № задания | |
| Ответ | -16 |
1. Может ли функция 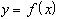
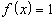
2. Может ли функция принимать каждое свое значение ровно 2 раза?
3. Может ли функция иметь два максимума и ни одного минимума?
4. Может ли функция возрастать на всей числовой оси и удовлетворять неравенству 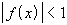
5. Может ли функция иметь максимум, но не иметь наибольшего значения?
6. Может ли значение в точке максимума быть меньше значения в точке минимума?
7. Может ли наибольшее значение функции быть меньше ее наименьшего значения?
8. Могут ли совпадать наибольшее и наименьшее значения функции?
9. Может ли функция принимать свое наибольшее значение в двух разных точках?
10. Может ли функция иметь два разных наибольших значения?
Цели урока: решение тестовых заданий базового уровня 
Ход урока:
Организационный момент.
Приветствие, сообщение темы и задач урока.
Организация решения тестовых заданий.
Учитель распределяет тестовые задания на четыре урока следующим образом:
Урок 93 Решение тестовых заданий базового уровня 
Урок 94 Решение тестовых заданий базового уровня 
Урок 95 Решение тестовых заданий более сложного уровня 
Урок 96 Решение тестовых заданий наиболее сложного уровня 
Учебно-тренировочные тестовые задания ЕГЭ
Тестовые задания базового уровня 
| А1. Производная элементарной функции | Ответы |
А1.1 Вычислите 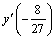 , если , если 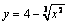 . A) 1 B) . A) 1 B) 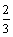 C) -1 D) — C) -1 D) — 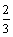 E) 3 E) 3 | А |
А1.2 Найдите 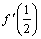 , если , если 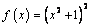 A) 2,5 B) -1 A) 2,5 B) -1 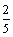 C) -1 C) -1 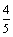 D) D) 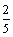 E) 1 E) 1 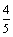 | А |
А1.3 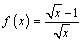 , , 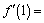 ? A) ? A) 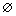 B) 2 C) 1 D) B) 2 C) 1 D) 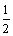 E) 3 E) 3 | Д |
А1.4 Найдите производную функции y = sin  x + cos x + cos  x A) 2sin2x B) 0 C) 4sinx D) sin4x E) 1 x A) 2sin2x B) 0 C) 4sinx D) sin4x E) 1 | В |
А1.5 Найти f’(a), если 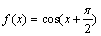 и и 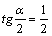 A) -0,6 B) A) -0,6 B) 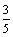 C) 0,8 D) C) 0,8 D) 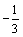 E) 0,4 E) 0,4 | А |
А1.6 Найдите 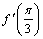 , если , если 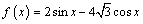 A) 7 B) -5 C) 2 + 4 A) 7 B) -5 C) 2 + 4 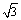 D) 2 D) 2 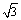 — 2 E) 5 — 2 E) 5 | А |
А1.7 Найдите производную функции: y = — 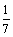 sin(7x — 5) A) — sin(7x — 5) A) — 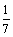 cos(7x — 5) B) -7cos(7x – 5) C) cos(7x — 5) D) -cos(7x — 5) E) -7cos7x cos(7x — 5) B) -7cos(7x – 5) C) cos(7x — 5) D) -cos(7x — 5) E) -7cos7x | Д |
| А1.8 y = 2 — cos2x. y ‘ = ? A) 2sin2x B) sin2x C) 4cos2x D) -sin2x E) -2sin2x | А |
А1.9 Найдите 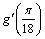 , если , если 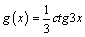 A) -2 B) A) -2 B) 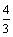 C) 4 D) — C) 4 D) — 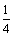 E) -4 E) -4 | Е |
А1.10 Найдите 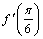 , если , если 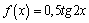 A) A) 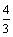 B) — B) — 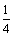 C) 4 D) 2 E) — C) 4 D) 2 E) — 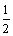 | С |
| А2.Производная сложной функции | Ответы |
А2.1 Найдите 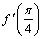 , если , если 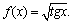 A) 1 B) A) 1 B) 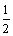 C) C) 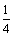 D) D) 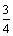 E) E) 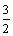 | А |
А2.2 Найти 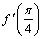 , если , если 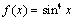 . A) . A) 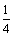 B) 1 C) B) 1 C) 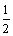 D) D) 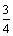 E) E) 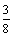 | В |
А2.3 Найдите 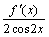 , если f(x) = sin , если f(x) = sin  2x A) sin2x B) cos2x C) -sin2x D) -cos2x E) 2sin2x 2x A) sin2x B) cos2x C) -sin2x D) -cos2x E) 2sin2x | E |
А2.4 Найдите 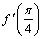 , если , если 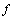 (x)= (x)= 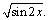 A) 0 B) 1 C) A) 0 B) 1 C) 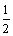 D) D) 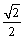 E) -1 E) -1 | А |
А2.5 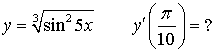 A) 3 A) 3 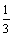 B) 1 B) 1 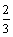 C) 2 D) 0 E) 2 C) 2 D) 0 E) 2 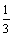 | Д |
А2.6 Найдите производную функции: 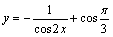 в точке в точке 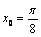 . A) . A) 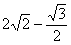 B) B) 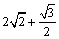 C) C) 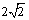 D) — D) — 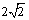 E) E) 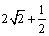 | Д |
А2.7 Вычислите 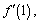 если если 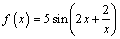 A) 5 B) 0 C) 2,5 D) — A) 5 B) 0 C) 2,5 D) — 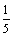 E) E) 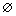 | В |
А2.8 Найдите производную функции 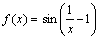 . A) . A) 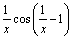 B) B) 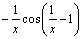 C) C) 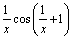 D) D) 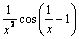 E) — E) — 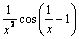 | Е |
А2.9 Найдите 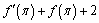 , если ?(x)=x·sin2x. A) 2 , если ?(x)=x·sin2x. A) 2 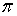 B) 2 C) 2+2 B) 2 C) 2+2 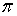 D) 2-2 D) 2-2 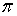 Е) 4 Е) 4 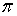 | С |
А2.10Найдите 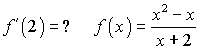 A) 0,625 B) 0,5 C) 0,25 D) -0,5 E) 1 A) 0,625 B) 0,5 C) 0,25 D) -0,5 E) 1 | А |
| А3. Критические точки, интервалы монотонности функции | Ответы |
А3.1 Найдите все интервалы убывания функции: 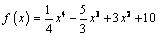 A) (2; 3) B) (- A) (2; 3) B) (- 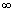 ; 0] и [2; 3] C) (- ; 0] и [2; 3] C) (- 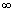 ; 3) D) (- ; 3) D) (- 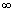 ; 0) и (3; ; 0) и (3; 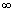 ) E) (- ) E) (- 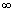 ; 0) и (2; ; 0) и (2; 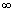 ) ) | В |
А3.2Найдите промежутки возрастания функции 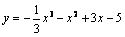 . A) (- . A) (- 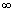 ; -1] и [3; ; -1] и [3; 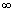 ) B) [-1; 3] C) [-3; 1] D) [1; 3] E) (- ) B) [-1; 3] C) [-3; 1] D) [1; 3] E) (- 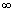 ; -3] и [1; ; -3] и [1; 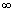 ) ) | С |
А3.3 Чему равна сумма всех целых значений аргумента функции f(x)= 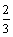 x x 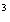 — 4x — 4x  + 3, при которых эта функция убывает? A) 9 B) 8 C) 10 D) 7 E) 11 + 3, при которых эта функция убывает? A) 9 B) 8 C) 10 D) 7 E) 11 | С |
А3.4Найти длину отрезка, на котором функция f(x) = -2x 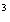 + 15x + 15x  + 12 возрастает. A) 5 B) 4 C) 6 D) 4,5 E) определить нельзя + 12 возрастает. A) 5 B) 4 C) 6 D) 4,5 E) определить нельзя | А |
А3.5Найдите суммарную длину промежутков возрастания функции y = f(x), если ее производная равна 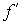 (x) = x(1 – x)(x (x) = x(1 – x)(x  – 7x + 10) A) 1 B) 3 C) 4 D) 6 E) 8 – 7x + 10) A) 1 B) 3 C) 4 D) 6 E) 8 | С |
А3.6 Все значения аргумента функции f(x) = 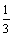 x x 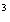 + 3x + 3x  , для которых эта функция убывает, отложены на оси ОХ. Какова длина получившегося отрезка? A) 4 B) 5 C) 6 D) 3 E) 7 , для которых эта функция убывает, отложены на оси ОХ. Какова длина получившегося отрезка? A) 4 B) 5 C) 6 D) 3 E) 7 | С |
А3.7Найдите значение функции f(x) = x 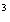 + 2,5x + 2,5x  — 2x в точке максимума. A) -8 B) 6 C) 10,5 D) -12 E) 14 — 2x в точке максимума. A) -8 B) 6 C) 10,5 D) -12 E) 14 | В |
А3.8Найдите сумму значений функции f(x) = 0,6x 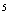 – 2x – 2x 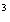 – 1 в точках максимума и минимума. A) -3 B) -2 C) -1 D) 1 E) 2 – 1 в точках максимума и минимума. A) -3 B) -2 C) -1 D) 1 E) 2 | В |
А3.9 Найдите разность между наименьшим и наибольшим значениями функции 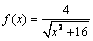 , заданной на отрезке [-3; 3]. A) -0,2 B) 0,2 C) 0,4 D) -0,8 E) 0,8 , заданной на отрезке [-3; 3]. A) -0,2 B) 0,2 C) 0,4 D) -0,8 E) 0,8 | А |
А3.10 Найдите сумму значений функции y = 3x 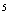 – 5x – 5x 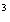 – 3 в точках экстремума. A) -9 B) -6 C) -8 D) -4 E) -2 – 3 в точках экстремума. A) -9 B) -6 C) -8 D) -4 E) -2 | В |
| А4. Наибольшее, наименьшее значение функции | Ответы |
А4.1 Найти наибольшее значение функции f(x) = 3x  — 4x — 4 на отрезке [0; 3]. A) 10 B) 20 C) 11 D) 16 E) 18 — 4x — 4 на отрезке [0; 3]. A) 10 B) 20 C) 11 D) 16 E) 18 | С |
А4.2 Найдите наибольшее значение функции 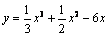 на отрезке [-1; 3]. A) 6 на отрезке [-1; 3]. A) 6 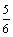 B) 6 B) 6 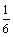 C) 6 D) 6,5 E) 6 C) 6 D) 6,5 E) 6 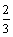 | В |
А4.3 Чему равна разность между наибольшим и наименьшим значениями функции f(x) = x 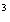 + 2x — 5 на отрезке [-1; 1] ? A) -6 B) 6 C) -5 D) 5 E) 4 + 2x — 5 на отрезке [-1; 1] ? A) -6 B) 6 C) -5 D) 5 E) 4 | В |
А4.4 Найдите наибольшее значение функции y = -2x  + 5x – 3. A) + 5x – 3. A) 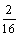 B) B) 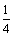 C) 5 D) -3 E) C) 5 D) -3 E) 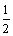 | А |
А4.5 Найдите наименьшее значение функции y = 2x 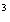 + 3x + 3x  — 12x на отрезке [0; 2]. A) 0 B) -2 C) -5 D) -7 E) -8 — 12x на отрезке [0; 2]. A) 0 B) -2 C) -5 D) -7 E) -8 | Д |
А4.6 Найдите разность между наибольшим и наименьшим значениями функции y = x 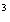 — 3x — 3x  + 1, заданной на отрезке [-1;4]. A) 20 B) 14 C) 15 D) 18 E) 16 + 1, заданной на отрезке [-1;4]. A) 20 B) 14 C) 15 D) 18 E) 16 | А |
А4.7 Найдите наименьшее значение функции 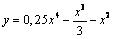 на луче [-2,5; на луче [-2,5; 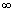 ). A) — ). A) — 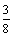 B) B) 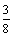 C) C) 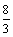 D) — D) — 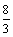 E) найти нельзя E) найти нельзя | Д |
А4.8 Найдите наибольшее значение функции 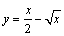 на отрезке [0; 16]. A) 4 B) 8 C) -3 D) 5 E) 12 на отрезке [0; 16]. A) 4 B) 8 C) -3 D) 5 E) 12 | А |
А4.9 Найдите наибольшее и наименьшее значение функции ?(x)=x  (x-6) на отрезке [-1; 3] A) 2; -4 B) 0; -32 C) 6; -21 D) 0; -27 Е) 6; -20 (x-6) на отрезке [-1; 3] A) 2; -4 B) 0; -32 C) 6; -21 D) 0; -27 Е) 6; -20 | Д |
А4.10 Найдите наименьшее значение функции y=3x  -12x-16 на отрезке [3; 8]. A) 18 B) -22 C) -25 D) -28 E) -30 -12x-16 на отрезке [3; 8]. A) 18 B) -22 C) -25 D) -28 E) -30 | С |
| А5. Уравнение касательной функции | Ответы |
А5.1 Угловой коэффициент касательной, проведенной к графику функции y = sin 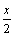 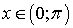 , в точке (x , в точке (x 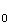 , y , y 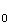 ) равен ) равен 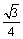 . Найдите x . Найдите x 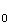 ? y ? y 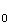 . A) . A) 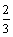 B) B) 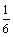 C) C) 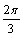 D) — D) — 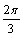 E) E) 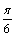 | Е |
А5.2 Какая из прямых параллельна касательной к кривой y = 4 – x  в точке x в точке x 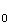 = 2? A) y = 4 – 4x B) y = 2x + 8 C) y = x + 8 D) y = 4x + 8 E) y = 8 – 4x = 2? A) y = 4 – 4x B) y = 2x + 8 C) y = x + 8 D) y = 4x + 8 E) y = 8 – 4x | А |
А5.3 При каких значениях x касательная к графику функции y = 2x 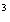 + 3x + 3x  — 6x параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 — 6x параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 | С |
А5.4В какой точке касательная, проведенная к графику функции y = x  — 2x + 1, параллельна прямой y = -4(x + 1)? A) (-1; — 2x + 1, параллельна прямой y = -4(x + 1)? A) (-1; 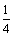 ) B) (-1; 4) C) (1; ) B) (-1; 4) C) (1; 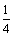 ) D) (1; 4) E) (0; 4) ) D) (1; 4) E) (0; 4) | В |
А5.5 Через точку A(1; 4) проходят две касательные к графику функции 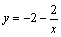 . Найдите сумму абсцисс точек касания. A) -1 B) 1 C) . Найдите сумму абсцисс точек касания. A) -1 B) 1 C) 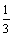 D) D) 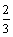 E) — E) — 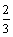 | Е |
А5.6Угловой коэффициент касательной, проведенной к параболе y = x  – 2x в ее точке (x – 2x в ее точке (x 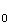 ; y ; y 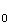 ), равен 4. Напишите уравнение этой касательной. A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 ), равен 4. Напишите уравнение этой касательной. A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 | Е |
А5.7 В какой точке графика функции 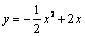 касательная к графику будет параллельна прямой, заданной уравнением y = -2x ? A) (-4; 0) B) (0; 4) C) (4; 0) D) (0; -4) E) (2; 4) касательная к графику будет параллельна прямой, заданной уравнением y = -2x ? A) (-4; 0) B) (0; 4) C) (4; 0) D) (0; -4) E) (2; 4) | С |
А5.8Найдите угловой коэффициент касательной, проведенной к окружности (x + 3)  + (y – 5) + (y – 5)  = 45 в ее точке A(0; 11). A) — = 45 в ее точке A(0; 11). A) — 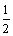 B) -2 C) B) -2 C) 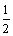 D) 2 E) D) 2 E) 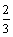 | А |
А5.9В какой точке касательная, проведенная к графику функции y = x  + 2x + 8, параллельна прямой y + 2x — 8 = 0? A) (-2; 8) B) (2; 8) C) (-2; -8) D) (2; -8) E) (0; 8) + 2x + 8, параллельна прямой y + 2x — 8 = 0? A) (-2; 8) B) (2; 8) C) (-2; -8) D) (2; -8) E) (0; 8) | А |
А5.10 Прямая y = -5x + 3 параллельна касательной к графику функции f(x) = x  — x. Найдите координаты точки касания. A) (-2; 6) B) (1; 0) C) (2; 4) D) (0; 0) E) (2; 2) — x. Найдите координаты точки касания. A) (-2; 6) B) (1; 0) C) (2; 4) D) (0; 0) E) (2; 2) | А |
Вариант I
1. Какое равенство не задает функцию?
а) y 2 = x 2 ; б) y = x 2 ; в) y = lg x; г) y = 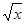
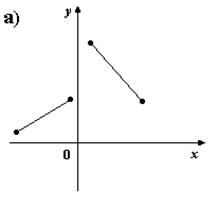
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
1) Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x)) ?
а) f(x) = tg(x), g(x) = arctg x; б) f(x) = 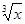
Видео:Математический анализ, 12 урок, Монотонность и экстремумы функцииСкачать

Может ли функция быть монотонной а при этом уравнение иметь два корня
Если — монотонная функция, то уравнение f(x)=a имеет не более одного корня.
Решить уравнение 
Решение. Левая часть данного уравнения – возрастающая функция (по свойству 1). Поэтому, согласно теореме, у него не более одного корня. При подстановке в уравнение x=7 получаем 3+2+1=6, это – верное равенство. Значит, x=7 — единственный корень.
Видео:Три уравнения на одну идею. Используем монотонность функций Алгебра 10-11Скачать

Теорема о корне при решении уравнений. Урок алгебры. 9-й класс
Разделы: Математика
Класс: 9
Цели урока:
- Использование особенностей монотонности функций для активизации творческого мышления учащихся.
- Формирование у школьников навыков применения теоремы о корне для решения уравнений.
- Умение обобщать, конкретизировать и анализировать изучаемый материал.
- Обучение учащихся нестандартным способам решения задач.
- Развитие логики и навыков самостоятельной работы.
- Воспитание ответственного отношения к учебному труду.
Тип урока: урок изучения нового материала.
Оборудование: учебник “Алгебра 9” (автор: Мордкович А. Г.), задачник “Алгебра 9” (авторы: Мордкович А. Г., Тульчинская Е.Е. и др.), книга для преподавателей “Алгебра 9” (авторы: Афанасьева Т.Л., Тапилина Л.А.), карточки с памяткой для самостоятельной работы по данной теме, компьютер, мультимедийный проектор, экран.
Предложенный урок расширяет программу по теме “Функции”. Учащиеся уже знакомы с основными свойствами функций, владеют навыками грамотного чтения графиков и умеют применять алгоритм исследования функций. На уроке основной упор делается на использование свойств монотонности функций для решения уравнений. Рассматривается теорема о корне. В ходе урока каждый учащийся должен достигнуть определенного уровня понимания материала, поэтому этап усвоения знаний разработан дифференцированно.
Ожидаемый результат по окончании изучения материала:
1-й уровень: каждый ученик должен знать геометрическую модель теоремы о корне и уметь установить связь монотонности функций, входящих в уравнение, с количеством корней соответствующего уравнения.
2-й уровень: каждый ученик должен знать алгоритм решения уравнений с использованием теоремы о корне и уметь применять ее для решения нестандартных задач.
На уроке рассматриваются различные виды уравнений, решаемых с помощью теоремы о корне. В дальнейшем учащимся предлагается использовать предложенный алгоритм в домашней контрольной работе (§16, задачник “Алгебра 9” авторы: Мордкович А. Г., Тульчинская Е.Е. и др.). Для организации проверочной работы используются задания из практикума (составитель автор).
Ход урока
I этап. Организационный момент (1 мин.).
II этап. Актуализация опорных знаний и умений (7 мин.).
Учитель: Необходимо повторить пройденное для того, чтобы успешно перейти к усвоению нового материала. На протяжении изучения темы “Функции” вы постепенно учились читать графики функций, используя алгоритм для их исследования. Остановимся на особенностях возрастающей и убывающей функций. Подборка материала подготовлена учащимися.
Выступление учащихся сопровождается показом презентации.
III этап. Объяснение нового материала (10 мин).
Учитель: Сегодня изучение нового материала мы начнем с доказательства теоремы о корне.
Теорема о корне.
Пусть функция y=f(x) возрастает (или убывает) на множестве 
Доказательство:
Рассмотрим возрастающую функцию f(x) (в случае убывающей функции рассуждения аналогичны). По условию на множестве X существует такое число b, что f(b)=a. Покажем, что b — единственный корень уравнения f(x)=a.
Допустим, что на множестве X есть еще число 
Геометрическая модель теоремы о корне может быть представлена как на экране, так и на плакате.
Учитель: Давайте вместе рассмотрим следующие примеры:
Сколько корней имеет уравнение?

— x 5 = 
Учащиеся отмечают, что на своих областях определения функция 
Учитель: Откроем учебник на 98 стр. и обратим внимание на то, что при решении уравнения x 5 =3-2x (пример 1, рис. 79) геометрическая модель наглядно иллюстрирует следствие, которое следует из теоремы о корне:
Следствие.
“Если функция y=f(x) возрастает, а функция y=g(x) убывает и если уравнение f(x)=g(x) имеет корень, то только один”.
По учебнику разбирается пример 1.
Опираясь на это утверждение, можем изящно решить уравнение
x 5 = 3 — 2x без чертежа, следуя следующему алгоритму:
- заметим, что при x=1 выполняется равенство 1 5 =3-2·1,
значит, x=1 – корень уравнения (этот корень мы угадали); - функция у = 3 — 2x убывает, а функция у = x 5 возрастает,
значит, корень у заданного уравнения только один и
этим корнем является значение x=1.
Учитель: Определим сколько решений имеет уравнение x 5 = — 3x +5 с комментированием на месте.
Решение:
- рассмотрим функции у = x 5 и у = — 3x + 5; заметим, что область определения этих функций одинакова: D(у)=(-
; +
);
- на D(у) функция у = — 3x + 5 убывает, а функция у = x 5 возрастает. Значит, по следствию из теоремы о корне, у заданного уравнения только один корень, т.е. уравнение, имеет одно решение.
Учитель: Цель нашего урока состоит в том, чтобы научиться решать задачи, используя теорему о корне (следствие).
На экране высвечивается обобщенный алгоритм решения уравнения f(x)=g(x) с использованием следствия из теоремы о корне:
- Определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b).
- Ввести две функции y=f(x) и y=g(x).
- Исследовать y=f(x) и y=g(x) на монотонность. Если y=f(x)возрастает (убывает), а y=g(x) убывает (возрастает), то уравнение f(x)=g(x) имеет единственный корень – x=b (ссылка на следствие).
IV этап. Усвоение новых знаний (23 мин.)
Учитель: Карточки и памятка для самостоятельной работы лежат у вас на столах. Приступим к выполнению заданий.
Так как нетрадиционные методы решения задач вызывают трудность у большинства учащихся, то следующее уравнение предлагается решить вместе. Для оформления решения учащийся по желанию выходит к доске (дается уравнение 2 уровня).
Решить уравнение: 
Решение: в начале запишем уравнение (3) в виде

затем воспользуемся теоремой о корне.
- при x=5 уравнение превращается в верное числовое равенство:
; 5=5 (т.е. угадали корень уравнения – x=5).
- заметим, что в левой части уравнения функция
возрастает на D(у)=[3; +
); значит, у заданного уравнения корень только один и этим корнем является значение x=5.
После того как данное задание выполнено, класс приступает к решению уравнений в зависимости от восприятия материала:
1) те, кто попытается справиться самостоятельно с не очень сложными уравнениями;
2) те, у кого решение уравнений не вызывает затруднений.
В соответствии с этим учащиеся получают дифференцированные задания.
1 уровень.
1. 
2. 
3. 
4. 
5. 
6. 
2 уровень.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
Необходимо проверить правильность выполнения заданий, поэтому от каждой группы выступает ученик, демонстрируя решение одного из уравнений на доске.
V этап. Итог урока (2 мин.).
Подводя итог урока, учитель и ученики выясняют трудности при решении уравнений и обсуждают, на что они должны обратить внимание при выполнении домашнего задания.
VI этап. Домашнее задание (1мин.).
Учитель: задание на дом следующее: доделать задания на карточках; если на уроке выполнено все, то воспользоваться дополнительной карточкой из материалов для самостоятельной работы; домашняя контрольная работа (§16, задачника “Алгебра 9”).
Заключительное слово учителя (1мин). Любовь к предмету не возникает просто так. Двигаясь постепенно от простого к сложному, анализируя и обобщая учебный материал, интересуясь “изящными” способами решения, можно понять красоту алгебры. Сегодня знание теории и практические навыки, что равнозначно, показали многие из вас. Особую благодарность заслуживают ребята, создавшие прекрасную презентацию. Постижение мира бесконечно: дерзайте, творите, ошибайтесь, ищите ответы на вопросы, только не “проспите” лучшие годы. “Жажда к жизни” – залог успеха.
Материалы к уроку для самостоятельной работы учащихся
1. Памятка по решению уравнений.
Теорема о корне.
Пусть функция y=f(x) возрастает (или убывает) на множестве 
Следствие.
“Если функция y=f(x) возрастает, а функция y=g(x) убывает и если уравнение f(x)=g(x) имеет корень, то только один”.
Алгоритм решения уравнения f(x)=a с использованием теоремы о корне:
- определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b);
- исследовать функцию y=f(x), стоящую в левой части уравнения, на монотонность. Если y=f(x) возрастает (убывает), то уравнение f(x)=a имеет единственный корень – x=b (ссылка на теорему).
Алгоритм решения уравнения f(x)=g(x) с использованием следствия из теоремы о корне:
Рекомендации:
Сначала, если это необходимо, уравнение привести к такому виду, чтобы было удобно исследовать на монотонность функции, стоящие в левой и правой частях уравнения, а затем следовать согласно следующему алгоритму:
- определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b);
- ввести две функции y=f(x) и y=g(x);
- исследовать y=f(x) и y=g(x) на монотонность. Если y=f(x) возрастает (убывает), а y=g(x) убывает (возрастает), то уравнение f(x)=g(x) имеет единственный корень – x=b (ссылка на следствие).
2. Практические задания.
Рекомендации: рассмотрим готовое решение уравнения (возможен такой вариант оформления).
Решить уравнение: 
Решение:
Функция f(x) = 

На основании теоремы о корне уравнение имеет не более одного корня.
Т.к. f (1) = 4, то x = 1 – корень уравнения.
Дополнительная карточка (подбор заданий [1]).






Литература.
- Ткачук В.В. Математика абитуриенту. – М.: МЦНМО, 2005.
💡 Видео
Монотонность функции - 2, параметр. ЕГЭ по математике, профиль, 18 задание.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Найдите все значения а, при каждом из которых уравнение 64x^6+4x^2=(3x+a)^3+3x+a не имеет корней.Скачать

Алгебра 10 класс. 9 сентября. Исследование функции на монотонность, используя свойства числовых неСкачать

Параметр. Серия 5. Что такое монотонная функция и как с ее помощью решать задачиСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Задачи с параметром: как использовать четность и монотонность? | Математика ЕГЭ 10 класс | УмскулСкачать

Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Параметры 10. Монотонность - часть 1 - теорияСкачать

Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумыСкачать

ЕГЭ 2024 по математике🔥№18. Параметры🔥 Монотонность. Метод xoa. МодулиСкачать

СВОЙСТВА ФУНКЦИИ — Промежутки Знакопостоянства и МонотонностиСкачать

Теория к ЕГЭ 4 | Теорема о корне | Использование монотонности при решении задач с параметромСкачать

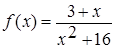
 ; +
; + ; 5=5 (т.е. угадали корень уравнения – x=5).
; 5=5 (т.е. угадали корень уравнения – x=5). возрастает на D(у)=[3; +
возрастает на D(у)=[3; +