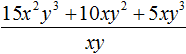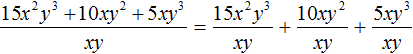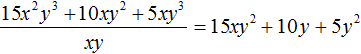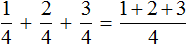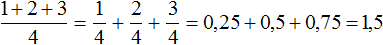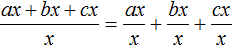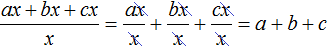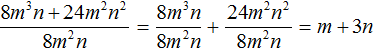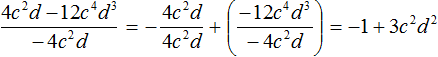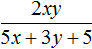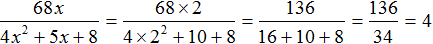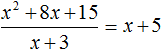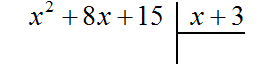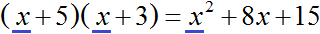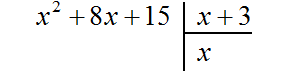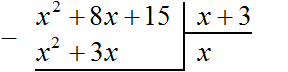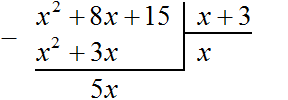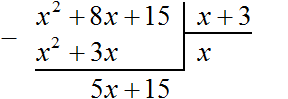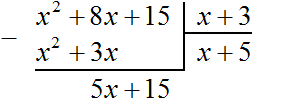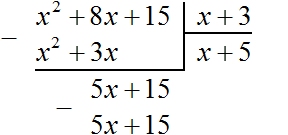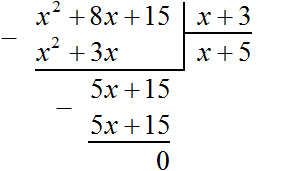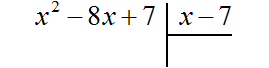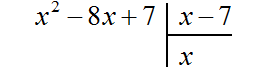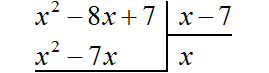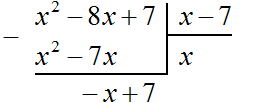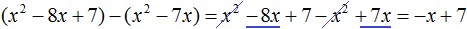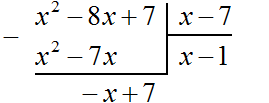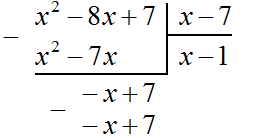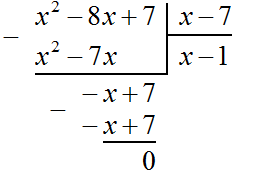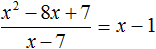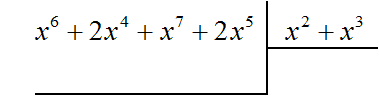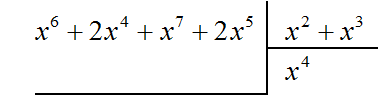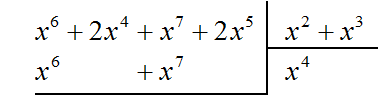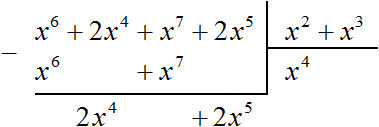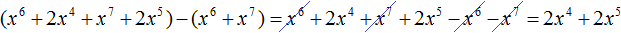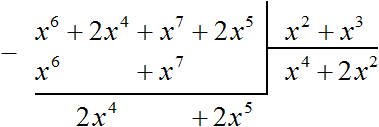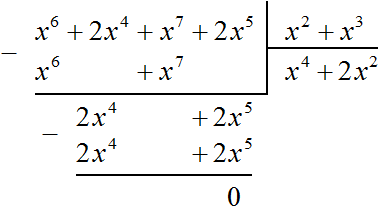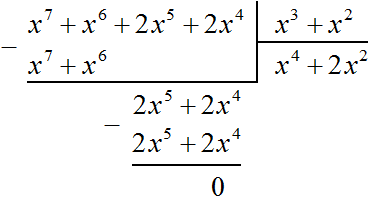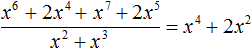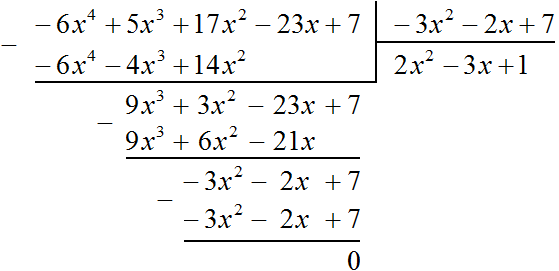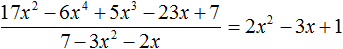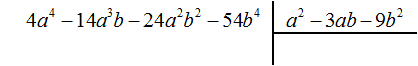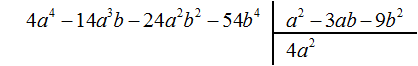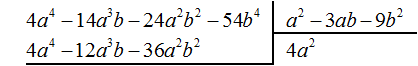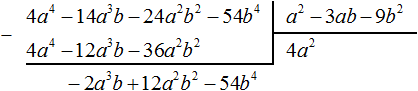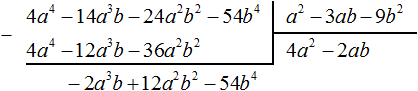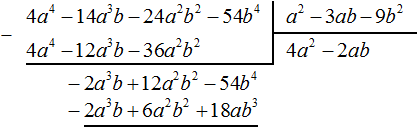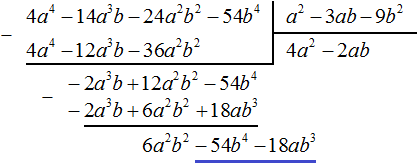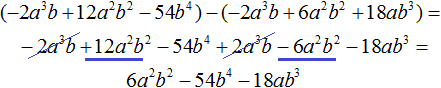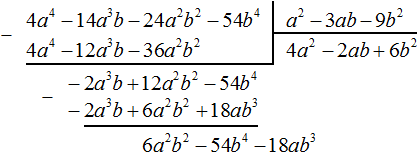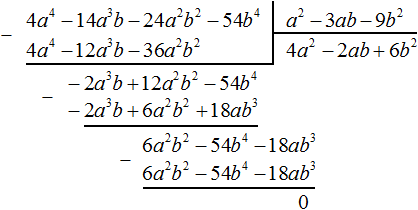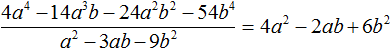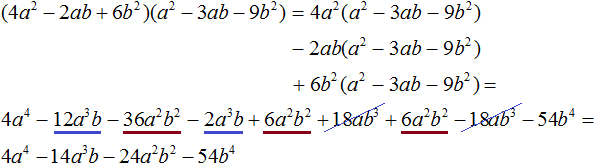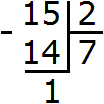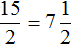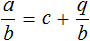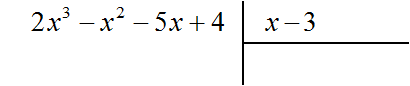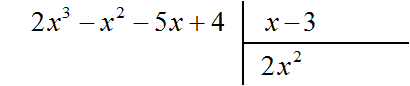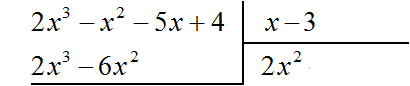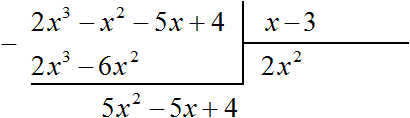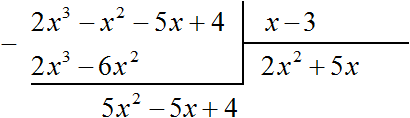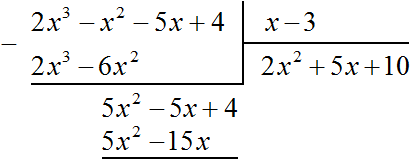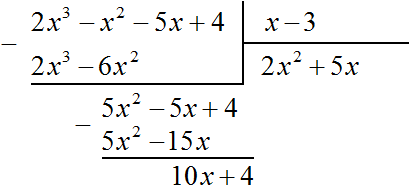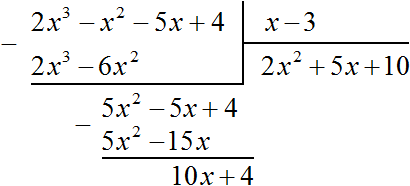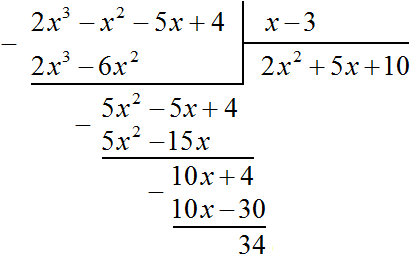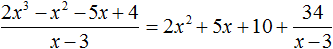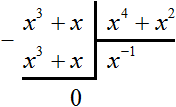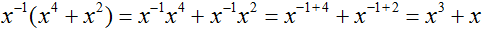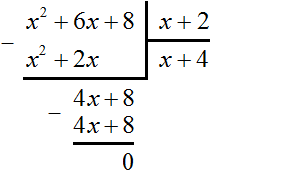- Деление с остатком.
- Остаток от деления
- Деление многочленов
- Деление многочлена на одночлен
- Деление одночлена на многочлен
- Деление многочлена на многочлен
- Деление многочлена на многочлен с остатком
- Когда деление многочленов невозможно
- Деление чисел с остатком
- Деление с остатком целых положительных чисел
- Проверка деления с остатком
- Деление с остатком положительного числа на целое отрицательное
- Деление с остатком целого отрицательного числа на целое положительное
- Деление с остатком целых отрицательных чисел
- Деление с остатком с помощью числового луча
- 🎦 Видео
Видео:Как делить числа с остатком? Деление на двузначное число с остатком.Скачать

Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:

Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Видео:Как решать уравнения с остатком. Математика 5 классСкачать

Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6 Category: 5 класс, Натуральные числа Leave a comment
Видео:Деление остатком. Как делить числа с остатком?Скачать

Деление многочленов
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать

Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy . Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy. Получающиеся частные будем складывать:
Получили привычное для нас деление одночленов. Выполним это деление:
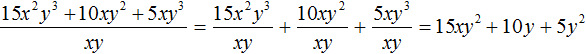
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy 2 + 10y + 5y 2 и делителя xy должно быть равно многочлену 15x 2 y 3 + 10xy 2 + 5xy 3 , то есть исходному делимому. Проверим так ли это:
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби 

Если мы вычислим выражение 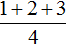

При этом выражение 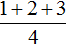
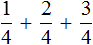
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x , образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m 3 n + 24m 2 n 2 на одночлен 8m 2 n
Пример 3. Разделить многочлен 4c 2 d − 12c 4 d 3 на одночлен −4c 2 d
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5 .
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy . Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy , поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения 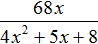
Выражение 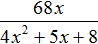
Видео:Деление в столбик с остатком. Как объяснить деление столбиком?Скачать

Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3 , получается многочлен x 2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x 2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5 .
Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x 2 + 8x + 15 на многочлен x + 3 . Так мы поэтапно увидим, как получается многочлен x + 5 .
В данном случае результат нам известен заранее. Это будет многочлен x + 5 . Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3 , мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5 .
Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x 2 ) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3 . На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3 , получается x 2 + 3x . Записываем этот многочлен под делимым x 2 + 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x 2 + 8x + 15 вычитаем x 2 + 3x . Подобные члены вычитаем из подобных им членов. Если из x 2 вычесть x 2 , получится 0 . Ноль не записываем. Далее если из 8x вычесть 3x , получится 5x . Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3 . Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x ) разделить на первый член делителя (это член x ). Если 5x разделить на x , получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3 . При умножении 5 на x + 3 , получается 5x + 15 . Записываем этот многочлен под делимым 5x + 15
Теперь из делимого 5x + 15 вычитаем 5x + 15 . Если из 5x + 15 вычесть 5x + 15 получится 0.
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3 , должен получаться многочлен x 2 + 8x + 15
Пример 2. Разделить многочлен x 2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x . Записываем x под правым углом:
Умножаем x на x − 7 , получаем x 2 − 7x . Записываем этот многочлен под делимым x 2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Вычитаем из x 2 − 8x + 7 многочлен x 2 − 7x . При вычитании x 2 из x 2 получается 0 . Ноль не записываем. А при вычитании −7x из −8x получается −x , поскольку −8x − (−7x) = −8x + 7x = −x . Записываем −x под членами −7x и −8x . Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7 . Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x ) разделить на первый член делителя (это член x ). Если −x разделить на x , получится −1 . Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7 , получаем −x + 7 . Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7 . Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x 2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним проверку. Умножим частное x − 1 на делитель x − 7 . У нас должен получиться многочлен x 2 − 8x + 7
Пример 3. Разделить многочлен x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x 4
Умножаем x 4 на делитель x 2 + x 3 и полученный результат записываем под делимым. Если x 4 умножить на x 2 + x 3 получится x 6 + x 7 . Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x 6 + x 7 . Вычитание x 6 из x 6 даст в результате 0. Вычитание x 7 из x 7 тоже даст в результате 0. Оставшиеся члены 2x 4 и 2x 5 снесём:
Получилось новое делимое 2x 4 + 2x 5 . Это же делимое можно было получить, выписав отдельно многочлен x 6 + 2x 4 + x 7 + 2x 5 и вычтя из него многочлен x 6 + x 7
Разделим многочлен 2x 4 + 2x 5 на делитель x 2 + x 3 . Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x 2 . Записываем этот член в частном:
Умножаем 2x 2 на делитель x 2 + x 3 и полученный результат записываем под делимым. Если 2x 2 умножить на x 2 + x 3 получится 2x 4 + 2x 5 . Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание многочлена 2x 4 + 2x 5 из многочлена 2x 4 + 2x 5 дало в результате 0, поэтому деление успешно завершилось.
В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x 6 + 2x 4 + x 7 + 2x 5 упорядочить в порядке убывания степеней, то получим многочлен x 7 + x 6 + 2x 5 + 2x 4 . А если члены многочлена x 2 + x 3 упорядочить в порядке убывания степеней, то получим многочлен x 3 + x 2
Тогда деление уголком многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 примет следующий вид:
Деление завершено. Таким образом, частное от деления многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 равно x 4 + 2x 2
Выполним проверку. Умножим частное x 4 + 2x 2 на делитель x 2 + x 3 . У нас должен получиться многочлен x 6 + 2x 4 + x 7 + 2x 5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Перепишем умножение (x 4 + 2x 2 )(x 2 + x 3 ) упорядочив члены многочленов в порядке убывания степеней.
Пример 4. Разделить многочлен 17x 2 − 6x 4 + 5x 3 − 23x + 7 на многочлен 7 − 3x 2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Пример 5. Разделить многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a 2 . Записываем 4a 2 в частном:
Умножим 4a 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a 4 − 12a 3 b − 36a 2 b 2
Теперь делим −2a 3 b + 12a 2 b 2 − 54b 4 на делитель a 2 − 3ab − 9b 2 . Разделим первый член делимого на первый член делителя, получим −2ab . Записываем −2ab в частном:
Умножим −2ab на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым −2a 3 b + 12a 2 b 2 − 54b 4
Вычтем из многочлена −2a 3 b + 12a 2 b 2 − 54b 4 многочлен −2a 3 b + 12a 2 b 2 − 18ab 3 . При вычитании подобных членов обнаруживаем, что члены −54b 4 и 18ab 3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a 3 b из −2a 3 b и 6a 2 b 2 из 12a 2 b 2 , а вычитание 18ab 3 из −54b 4 запишем в виде разности −54b 4 − (+18ab 3 ) или −54b 4 − 18ab 3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче. Разделим 6a 2 b 2 − 54b 4 − 18ab 3 на делитель a 2 − 3ab − 9b 2 . Делим первый член делимого на первый член делителя, получим 6b 2 . Записываем 6b 2 в частном:
Умножим 6b 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым 6a 2 b 2 − 54b 4 − 18ab 3 . Сразу вычтем этот полученный результат из делимого 6a 2 b 2 − 54b 4 − 18ab 3
Деление завершено. Таким образом, частное от деления многочлена 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2 равно 4a 2 − 2ab + 6b 2 .
Выполним проверку. Умножим частное 4a 2 − 2ab + 6b 2 на делитель a 2 − 3ab − 9b 2 . У нас должен получиться многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Деление многочлена на многочлен с остатком
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное число 
Например, если при делении многочлена a на многочлен b получится частное c , да еще останется остаток q , то ответ будет записан так:
Например, разделим многочлен 2x 3 − x 2 − 5x + 4 на многочлен x − 3
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x 2 . Записываем 2x 2 в частном:
Умножим 2x 2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x 3 − 6x 2
Теперь делим 5x 2 − 5x + 4 на делитель x − 3 . Разделим первый член делимого на первый член делителя, получим 5x . Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x 2 − 5x + 4
Вычтем из многочлена 5x 2 − 5x + 4 многочлен 5x 2 − 15x
Теперь делим 10x + 4 на делитель x − 3 . Разделим первый член делимого на первый член делителя, получим 10 . Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4 . Сразу вычтем этот полученный результат из делимого 10x + 4
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4 , является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34 .
Поэтому при делении многочлена 2x 3 − 2x 2 − 5x + 4 на многочлен x − 3 получается 2x 2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Видео:3 класс. Математика. Деление с остаткомСкачать

Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x 3 + x на многочлен x 4 + x 2 , поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x 3 + x на многочлен x 4 + x 2 , и даже получить частное x − 1 , которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x − 1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x − 1 это дробь 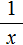
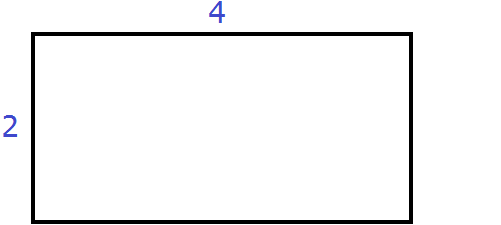
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
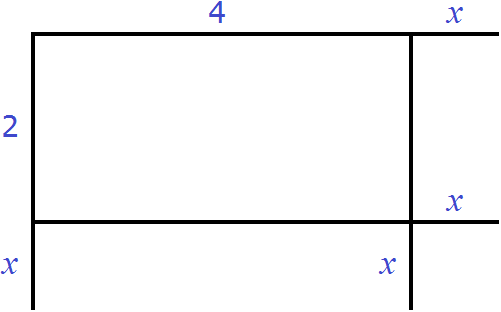
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
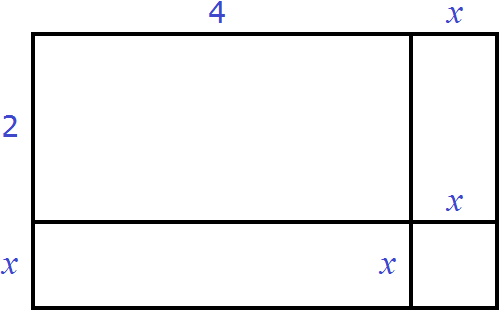
Теперь прямоугольник имеет длину x + 4 и ширину x + 2 . Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x 2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x 2 + 6x + 8 на ширину x + 2 и получить длину x + 4 .
Степень многочлена x 2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2 , а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Деление чисел с остатком
О чем эта статья:
Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Теорема
a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r
Видео:НЕВОЗМОЖНОЕ УРАВНЕНИЕ | Даже не пробуйте решитьСкачать

Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Видео:Как решать квадратные уравнения?Скачать

Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:
r = a − b * q
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Видео:Математика 5 класс (Урок№17 - Деление с остатком.)Скачать

Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
r = a − b * q
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
Видео:8 класс, 31 урок, Деление с остаткомСкачать

Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
🎦 Видео
РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Проверь свои знания по математике за 11 классСкачать

Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Как решают уравнения в России и СШАСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать