Теория Линдемана.
В элементарном акте мономолекулярной реакции участвует всего одна молекула. В соответствии с теорией активных столкновений реакция начинается со встречи двух активных молекул. Количество столкновений пропорционально квадрату концентраций. Поэтому, казалось бы, что мономолекулярные реакции, как и бимолекулярные, должны иметь порядок, равный двум. Но многие мономолекулярные реакции описываются уравнением первого порядка, причем порядок реакции может изменяться при изменении концентрации (давления) и быть дробным.
Объяснение механизмов газовых мономолекулярных реакций дано Линдеманом. Он предположил, что после столкновения активные молекулы могут не только распадаться на продукты реакции, но и дезактивироваться. Механизм реакции представляется двухстадийным:
1) A+A
2)
A 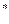
На первом этапе происходит перераспределение энергии, в результате чего одна молекула становится активной, а другая дезактивируется.
На второй стадии оставшиеся активные молекулы мономолекулярно превращаются в продукты реакции.
Рассмотрим стационарный процесс:
Выразим концентрацию активной частицы А * : 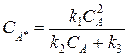
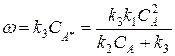
Анализ уравнения Линдемана:
1. СА – очень маленькая. В этом случае промежутки между столкновениями молекул настолько велики, что дезактивация происходит редко. Распад активных молекул на продукты происходит без затруднений; лимитирующей стадией является стадия активации. В связи с этим в уравнении Линдемана пренебрегаем в знаменателе 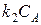
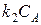
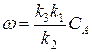
3. СА – средняя. В этом случае мономолекулярные реакции могут иметь дробный порядок (1
Дата добавления: 2019-10-16 ; просмотров: 455 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Теория активных соударений
Читайте также:
|
 |
 |
 |




Чтобы реакции перейти из 1 в 2, она должна преодолеть энергетически наиболее выгодную точку Р.
Если сделать “срез” потенциальной поверхности вдоль пути реакции и развернуть на плоскости то получится следующая диаграмма:
 |

Основное уравнение теории активированного комплекса имеет вид:
где kB = 1.38 . 10 -23 Дж/К — постоянная Больцмана, h = 6.63 . 10 -34 Дж . с — постоянная Планка, K ≠ — константа равновесия образования активированного комплекса, выраженная через молярные концентрации (в моль/л), χ – трансмиссионный коэффициент, учитывающий долю активированных комплексов, распадающихся на продукты.
Энтальпия и энтропия активации. Физический смысл
Уравнение изотермы: DG ¹ = –RTlnK ¹ ,
K ¹ = e – D G ¹ / RT ,
K ¹ = e – D H ¹ / RT × e D S ¹ / R ,
k = χ×(kвT/h)× e – D H ¹ / RT × e D S ¹ / R ,
где DH ¹ и DS ¹ — энтальпия и энтропия активации.
Из теории активных соударений уравнение для константы скорости:
k = PZ ×e – E/ RT , отсюда: P = (χ×(kвT/h)× e D S ¹ / R ) / Z, т.е. стерический фактор Р является энтропийным.
Дата добавления: 2015-04-20 ; просмотров: 24 | Нарушение авторских прав
Видео:Химия | Молекулярные и ионные уравненияСкачать

Мономолекулярные реакции в так анализ уравнения эйринга
В истории химической кинетики мономолекулярные реакции занимают особое место. Ещё Вант — Гофф изучая разложение AsH 3 и PH 3 в газовой фазе отнёс эти реакции к мономолекулярным. Однако, позднее было обнаружено, что разложение этих веществ протекает на стенке, а не в объеме (реакция Марша). В начале 20-х годов XX в. Первый порядок был открыт для разложения N 2 O 5 , но механизм оказался сложнее. Только в 1922 была обнаружена первая мономолекулярная газовая реакция – изомеризация циклопропана в пропилен.
Широко известная теория ТАС, однако не давала представлений о способе активации частиц в мономолекулярных реакциях.
В 1922 г. Предложил оригинальную гипотезу о путях активации частиц в мономолекулярных реакциях.
В соответствии со схемой Линдемана первая стадия взаимодействия – бимолекулярное столкновение частицы А с любой частицей в реакционной смеси:
Затем часть активированных частиц А * переходят в продукт реакции:
Поскольку концентрация А * мала её можно считать стационарной и используя метод стационарных состояний:
dC A * dt = k 1 C A 2 — k -1 C A C A * — k 2 C A * =0
При записи этого выражения предполагалось, что СА = СМ. Таким образом, СА легко находятся:
С A * = k 1 C A 2 k 2 + k -1 C A
Таким образом, скорость накопления продукта:
W = k 2 k 1 C A 2 k 2 + k -1 C A = k 2 k 1 k -1 C A 2 k 2 k -1 + C A = k ∞ C A k 2 k -1 + C A C A = k | C A
где
k | = k ∞ C A k 2 k -1 + C A
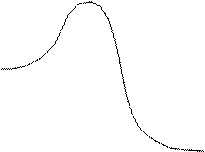
Общий вид k ′ = f ( CA ) приведем на рисунке:
Зависимость наблюдаемой константы скорости мономолекулярной реакции от концентрации реагирующего вещества.
Такие экспериментальные зависимости получили неоднократное подтверждение. Однако количественный анализ констант скорости в модели Линдемана неоднократно обнаруживал существенные расхождения теоретических и экспериментальных величин.
Хиншельвуд одним из первых понял, что рассматривать бесструктурные модели реагирующих частиц некорректно.
Главная идея Хиншельвуда заключалась в том, что наряду с некоторой энергией, которая в результате неупругих столкновений переходит во внутреннюю колебательно-вращательную эти молекулы сами «активированы» за счёт собственного запаса внутренней энергии. Это предположение внесло существенные коррективы в схему Линдемана. Если в схеме Линдемана активация протекает путём повышения кинетической энергии по центров над пороговым уровнем энергии εа, то в модели Хиншельвуда порог СА* может быть повышен и путём перераспределения собственной энергии колебания.
Для процессов дезактивации и химического превращения константы этих процессов в теории Хиншельвуда принимаются постоянными.
Итак, по Хиншельвуду после бимолекулярного столкновения частица А активируется в узко интервале энергий [ε, ε+ d ε]:
Если при столкновении участвуют f – колебательных степеней свободы, то полной колебательной и поступательной энергии в процессе отвечают:
S =2 f +2 f = S 2 -1
Вероятность попадания энергии молекулы, которая выражается f — квадратичными членами, в интервале ε, ε+ d ε
P ε + dε = ε kT f f ! e — ε kT d ε kT
Вероятность того, что ε ≥ kT
P ε ≥ ε a = ε a kT ∞ ε kT f f ! e — ε kT d ε kT
Если ε a kT ≪1 
P ε ≥ ε a = ε a kT f f ! e — ε a kT
Таким образом, учёт внутренних степеней свободы приводит к увеличению квадратичных членов и доля молекул с ε a ≥ ε a * 

N a N = Z a Z = 1 1 2 S -1 ! ε a kT S 2 -1 e — ε a kT
Очевидно при S =2 это выражение переходит в больцмановский множитель.
Схема Линдемана модифицированная Хиншельвудом приобретает следующий вид:
P – высокое k ∞ = k 1 k 2 k -1 = k 2 1 2 S -1 ε a RT 1 2 S -1 e — ε a RT
P – низкое k 1 = Z 0 1 1 2 S -1 ! ε a RT 1 2 S -1 e — ε a RT
Зависимость эффективной константы скорости k 1 , от давления получается комбинированием уравнения Линдемана и выражения Хиншельвуда:
k 1 = k 1 1+ k 2 k -1 C A ∙ 1 1 2 S -1 ! ∙ ε a RT 1 2 S -1 ∙ e — ε a RT
В 1927 г. Райнс и Ратснергер и в 1928 г. Кассель внесли новый элемент в теорию мономолекулярных реакций. Они записали схему Линдемана в виде:
После соударения А # имеет ε * > ε a 
k 2 = k ≠ ε * — ε a ε * f -1
где ε a 
а ε * 

f – общее число осцилляторов в активированной частице.
Эта теория предсказывала значния k ≠ 
10 13 с -1 
10 15 ÷ 10 17 c -1 
В 1951 – 1952 гг. Маркус видоизменил и дополнил модель РРК с использованием квантово – механического подхода.
По Маркусу ε * 





Применяя методы статистической термодинамики Маркусом было получено уравнение, с точностью до множителя совпало с уравнением, полученным в рамках теории переходного состояния. Это практически укрепило эти две теории. Кроме того, теория РРКМ дала объяснение большим значениям Р для многих мономолекулярных реакий.
Однако при расчёте констант мономолекулярных реакций необходима модель А * и A ≠ 

🔍 Видео
Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Кинетика || Лекция 20 || Теория переходного состояния, уравнение Эйринга, истинная энергия активацииСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

ЛЕКЦИЯ №16 || Химическая кинетика || Теория переходного состояния, вывод уравнения ЭйрингаСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

Решение задач на термохимические уравнения. 8 класс.Скачать

ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Кинетика || Лекция 4 || Реакции второго порядка, общий интеграл кинетического уравненияСкачать

Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Обратимая реакция второго порядка || Вывод уравнения || Разбор задачи || КинетикаСкачать

Химические уравнения. СЕКРЕТНЫЙ СПОСОБ: Как составлять химические уравнения? Химия 8 классСкачать

25. Схема реакции и химическое уравнениеСкачать

Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

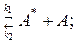
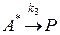
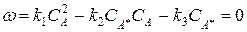


 A + A
A + A  A* + A
A* + A
 А + ВС [А…В…С] ¹ АВ + C
А + ВС [А…В…С] ¹ АВ + C 1 А + ВС
1 А + ВС






 60
60



















