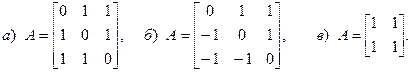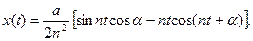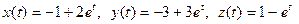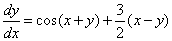Страницы работы
Содержание работы
Файл МоделиСАМРаботы02САМ06а.doc 5 стр. 200 Кбайт
1. Решение дифференциального уравнения различными методами, доступными SIMULINK.
Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью
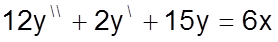
При использовании SIMULINK это уравнение можно решить несколькими способами.
Первый способ решения.
а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной
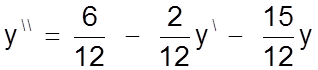
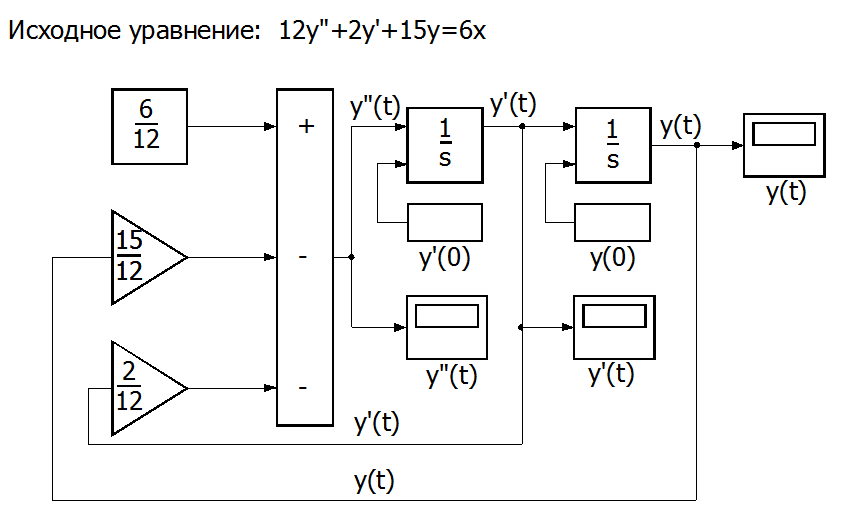
Полученное решение в модулях SIMULINK можно изобразить в виде
Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].
Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.
Вторая производная, согласно П7.02, должна получится путем вычитания из y0 равного 6/12, производных, умноженных на соответствующие коэффициенты.
Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «y(t)».
b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.
Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.
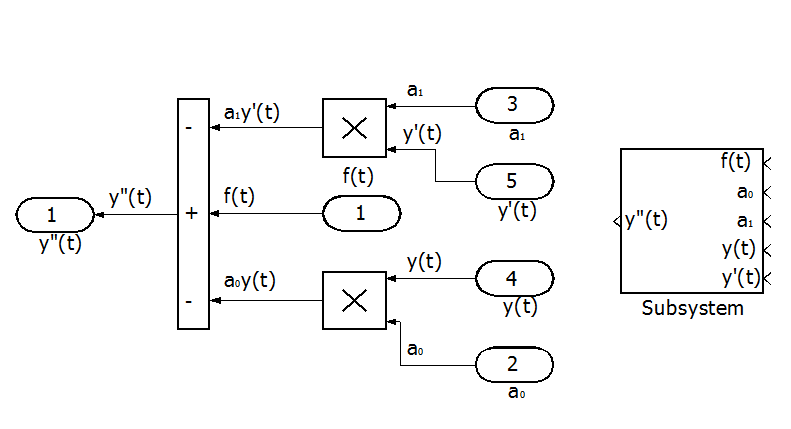
Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.
Рис. П7.2. Блок-схема решения правой части уравнения.
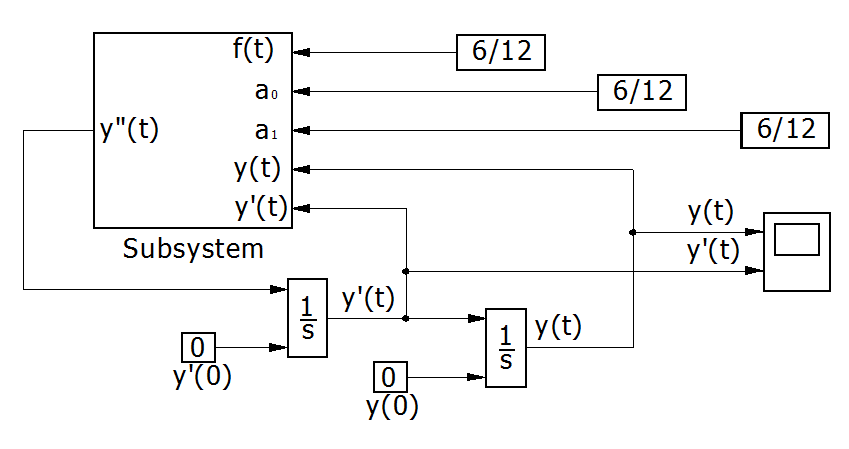
Составим блок-схему решения уравнения с использованием подсистемы.
Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].
Второй способ решения.
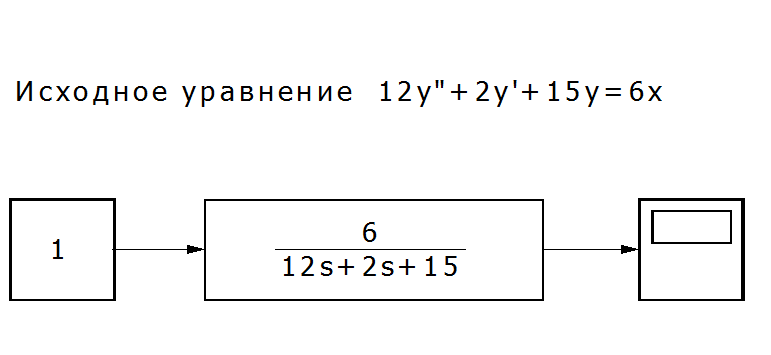
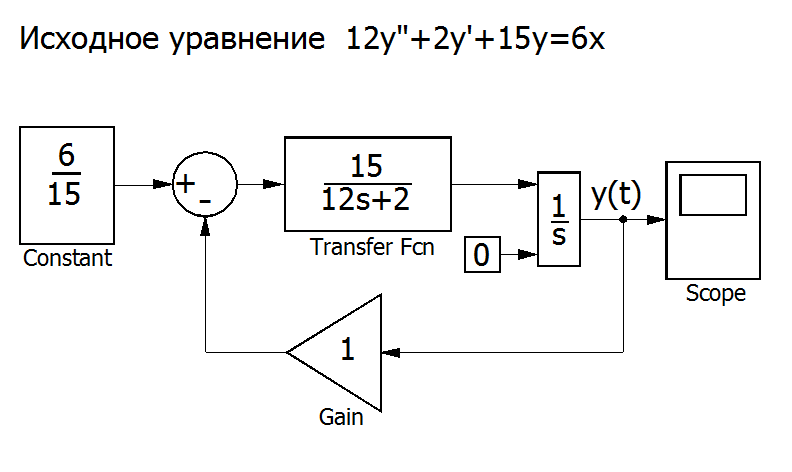
Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s — источники]
Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].
Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «Интеграл».
Третий способ решения.
SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.
Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].
Проведем исследование дифференциального уравнения 2 порядка
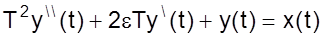
методами фазовой плоскости, используя возможности SIMULINK.
Начнем с того, что разрешим уравнение относительно старшей производной.
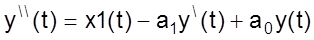
Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.
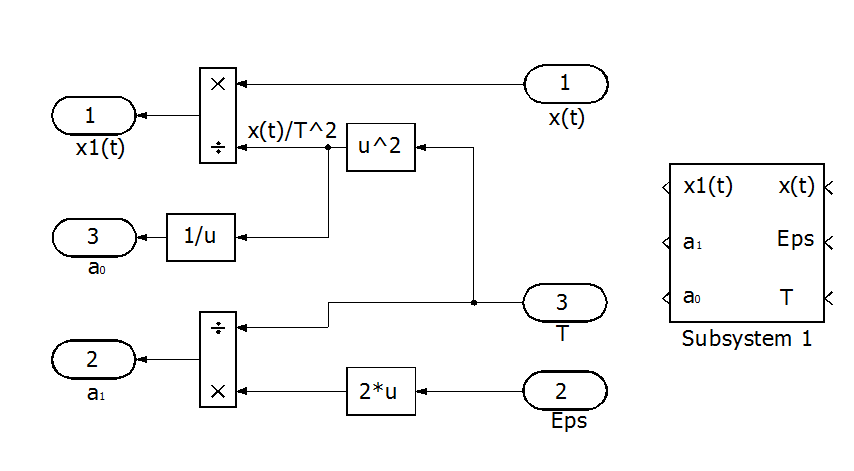
Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.
Рис. П8.1 Блок-схема формирования коэффициентов уравнения.
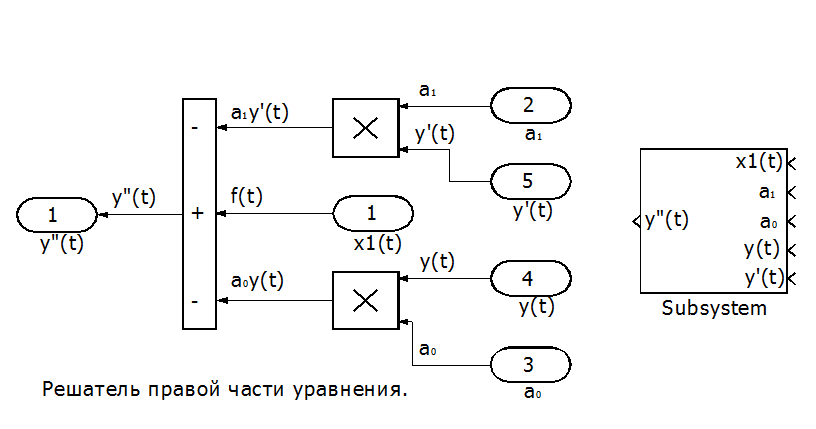
Рис. П8.2. Решатель правой части уравнения.
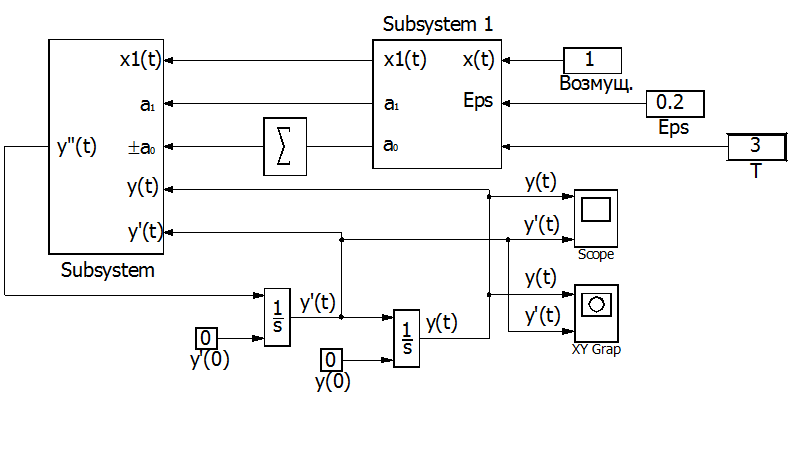
Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид
Рис. П8.3. Блок-схема решения дифференциального уравнения[5].
Исследование фазового портрета.
Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.
Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x — значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости. Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр. 485-495».
Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.
Рассмотрим следующие случаи характерные для уравнения 2 порядка:
[1] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris1»
[2] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris3»
[3] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris4»
[4] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris5»
[5] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p8ris3»
Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дата добавления: 2015-06-12 ; просмотров: 8133 ; Нарушение авторских прав
Цель работы: освоение методики моделирования линейных дифференциальных уравнений в системе MATLAB и SIMULINK.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Линейное дифференциальное уравнение.
Многие физические процессы, такие как колебания маятника, движение стрелки гальванометра, изменение высоты при посадке самолета, процессы в электрическом колебательном контуре могут быть описаны линейным однородным дифференциальным уравнением второго порядка
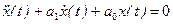
Здесь а0, а1 – постоянные коэффициенты, определяющие характер процесса, точкой обозначается производная по времени. Амплитуда переменной x(t) зависит от начальных условий, например, от начального отклонения x0 маятника и его начальной скорости 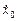
Вид теоретического решения дифференциального уравнения (1) определяется корнями его характеристического полинома
Если корни вещественные и различные р1 = a1`, р2 = a2`, то решение имеет вид
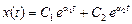
Если корни комплексные р1,2 =a ± ib , то решение имеет вид
Постоянные С1 и С2 находят, подставляя начальные условия в выражения для x(t) и 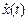
Пример 1. Дано дифференциальное уравнение
Его характеристическое уравнение p 2 + 2p + 2 = 0 имеет корни 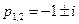
Дифференцируя, находим выражение для 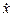
При t = 0 с учетом начальных условий получаем C1 = 2, С2 = 1. Следовательно,
Эффективным средством решения дифференциальных уравнений является численное моделирование в одном из математических пакетов (MATHCAD, MATLAB, SIMULINK и др.). График решения x(t) наблюдается на экране дисплея. В пакете MATLAB для этой цели имеются команды initial, lsim, ode23, ode45, dsolve. Дополнительныe возможности для пользователя предоставляет моделирование в SIMULINK.
1.2. Структурное моделирование линейных дифференциальных уравнений.
При структурном моделировании дифференциальных уравнений в пакете SIMULINK необходимо составить схему моделирования. На ней изображаются вычислительные блоки (усилители, сумматоры, интеграторы) и связи между ними. При проведении моделирования эта схема набирается на экране дисплея с помощью мыши или клавиатуры. По своему смыслу этот процесс аналогичен вводу программы, однако он более прост и нагляден. Подробная информация о реализации таких схем в SIMULINK имеется в разделе 3 учебного пособия Мироновского Л.А., Петровой К.Ю. «Введение в MATLAB» (ГУАП, 2006).
Рассмотрим методику составления схемы моделирования на примере однородного линейного дифференциального уравнения второго порядка
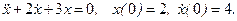
Для построения схемы моделирования воспользуемся методом понижения производной (методом Кельвина). В нем можно выделить четыре шага.
Шаг 1. Разрешаем исходное уравнение относительно старшей производной. В частности для уравнения (2) получаем 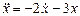
Шаг 2. Полагаем старшую производную известной и выполняем ее последовательное интегрирование, получая все низшие производные и саму переменную х. В случае уравнения (2) для этого потребуется два последовательно включенных интегратора, на выходах которых получим сигналы 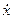
Шаг 3. Формируем старшую производную, используя уравнение, полученное на первом шаге. В нашем примере для этого потребуется сумматор, складывающий сигналы 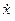
Шаг 4. Объединяем схемы, полученные на втором и третьем шагах, в общую схему моделирования, указываем начальные условия интеграторов.
Применение этой методики для уравнения (2) приводит к схеме, показанной на рис. 1. Она содержит два интегратора, два масштабных усилителя и сумматор (обозначен кружочком).
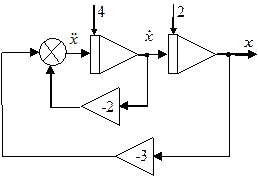 Рис. 1. Схема моделирования уравнения (2) Рис. 1. Схема моделирования уравнения (2) |
Выходной сигнал схемы подается на имитатор осциллографа (блок Scope) или передается в рабочее пространство MATLAB (блоки OUT или ToWorkspase).
1.3. Системы линейных дифференциальных уравнений первого порядка.
Многие технические объекты можно описать системой n линейных дифференциальных уравнений первого порядка:
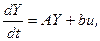
где и – входной сигнал; Y – вектор-столбец выходных переменных yi; b – вектор-столбец коэффициентов bi; A – квадратная матрица коэффициентов aij, 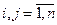
Например, при моделировании летательного аппарата составляющими вектора Y могут быть текущие координаты самолета и скорости их изменения, тогда матрица A будет характеризовать динамику самолета, а слагаемое bи описывать управляющие воздействия, формируемые летчиком или автопилотом.
Один из методов решения системы дифференциальных уравнений основан на предварительном переходе от системы (3) к одному уравнению n-го порядка. Для этого из уравнений системы и из уравнений, полученных их дифференцированием, исключают все переменные кроме одной. Для нее получают одно дифференциальное уравнение. Решая его, определяют эту переменную, а остальные находят, по возможности, без интегрирования.
Пример 2. Дана система из двух дифференциальных уравнений
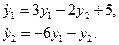
После дифференцирования первого уравнения получаем:
Чтобы исключить у2, вычтем отсюда удвоенное первое уравнение системы (4):
Мы получили линейное неоднородное дифференциальное уравнение второго порядка. Общее решение этого уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения 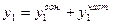
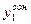
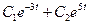
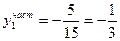
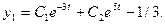
Для определения постоянных коэффициентов С1 и С2 используют начальные условия системы. Аналогичным образом этот метод применяется и для систем уравнений более высоких порядков
1.4. Моделирование системы линейных дифференциальных уравнений.
Если задача описывается системой дифференциальных уравнений первого порядка, то для ее моделирования по методу понижения производной достаточно составить схемы для каждого уравнения отдельно. Например, схема моделирования системы уравнений (4) будет иметь вид, показанный на рис. 2.
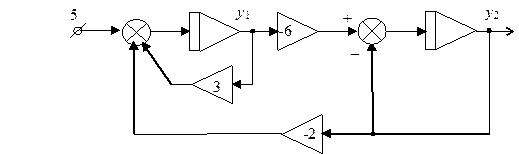 Рис. 2. Схема моделирования системы уравнений (4) Рис. 2. Схема моделирования системы уравнений (4) |
Для наблюдения графиков сигналов у1(t), у2(t) в SIMULINK используется блок осциллографа SCOPE, а для наблюдения фазовой траектории у2 = f (у1) – блок осциллографа XY Graph.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Теоретическое решение уравнения (1) при заданных значениях а0, а1 и начальных условиях x(0) = 5, 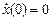
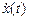
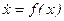
2. Схема моделирования заданного уравнения применительно к SIMULINK.
Теоретическое решение системы дифференциальных уравнений (3) для случая
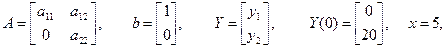
Схема моделирования исходной системы уравнений применительно к SIMULINK.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Набрать в SIMULINK схему моделирования уравнения (1), установить коэффициенты и начальные условия.
- Получить осциллограммы x(t),
и
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Набрать схему моделирования системы уравнений (3), установить коэффициенты и начальные условия (5).
- Получить осциллограммы у1(t), у2(t) и у2 = f(y1), сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Выполнить моделирование системы уравнений (3) в MATLAB, используя команду lsim. Cравнить графики, полученные в MATLAB и SIMULINK.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
- Решить следующие линейные дифференциальные уравнения:
а)
б)
- При каком значении а и при каких начальных условиях решение уравнения
имеет вид:
- В чем заключается метод понижения производной? Пользуясь этим методом, составить схемы моделирования для всех вариантов п.1.
- Используя метод понижения производной, составить схемы моделирования следующих дифференциальных уравнений:
а) 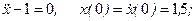
в)
г)
- Схема моделирования представляет собой кольцо из трех интеграторов с единичными коэффициентами и одинаковыми начальными условиями. Найти моделируемое дифференциальное уравнение и его аналитическое решение.
- Как изменятся графики решения линейного однородного дифференциального уравнения при замене знаков всех начальных условий на противоположные?
- Описать процедуру перехода от системы дифференциальных уравнений к одному уравнению и обратную процедуру, рассмотрев случай n=3. Привести пример.
- Составить схему моделирования и найти решение системы линейных дифференциальных уравнений
если матрица A имеет вид
ВАРИАНТЫ ЗАДАНИЙ ПО РАБОТЕ № 2
| № | ||||||||||||
| a1 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,6 |
| a0 | 0,4 | 1,6 | 4,8 | 0,5 | 1,8 | 5,0 | 0,6 | 2,0 | 5,4 | 0,7 | 2,2 | 5,8 |
| a11 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -0,9 | -0,9 | -0,9 | -0,9 | -0,9 |
| a12 | 1,0 | 0,8 | 0,7 | 0,6 | 0,57 | 0,4 | 0.35 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 |
| a22 | -2,0 | -1,8 | -1,7 | -1,6 | -1,5 | -1,4 | -1,3 | -1,9 | -1,7 | -1,6 | -1,5 | -1,4 |
| № | ||||||||||||
| a1 a0 | 0,1 0,8 | 0,3 2,4 | 6,0 | 0,9 8,8 | 0,1 0,9 | 0,3 2,6 | 0,7 6,4 | 1.1 9,0 | 0,2 1,0 | 0,3 2,8 | 0,8 6,8 | 0,6 5,8 |
| a11 | -0,9 | -0,9 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,5 | -0,5 | -0,5 |
| a12 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 | 0,6 | 0.5 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 |
| a22 | -1,3 | -1,6 | -1,6 | -1,6 | -1,5 | -1,4 | -1,3 | -1,2 | -1,1 | -1,5 | -1,3 | -1,2 |
Ответы на контрольный вопрос 1а,б,в,г:
а. 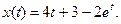
в.
г.
Видео:ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Моделирование дифференциальных уравнений в simulink
Дифференциальные уравнения и системы уравнений
Необходимо решить уравнение:
Попробуем решить его с помощью программы Simulink пакета MATLAB.
Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp . В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.
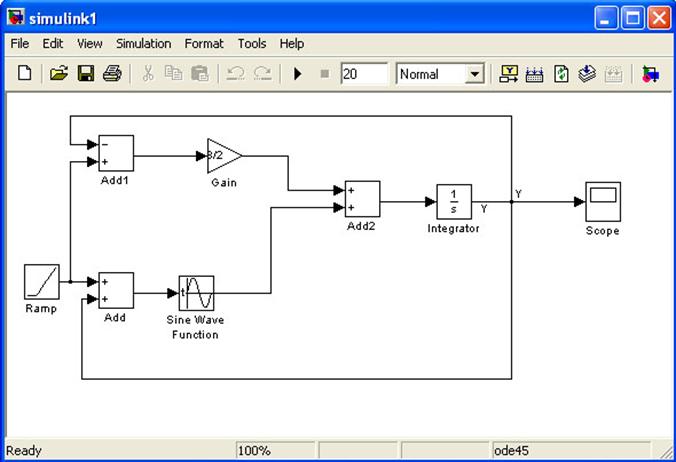
Решение уравнения выглядит так:
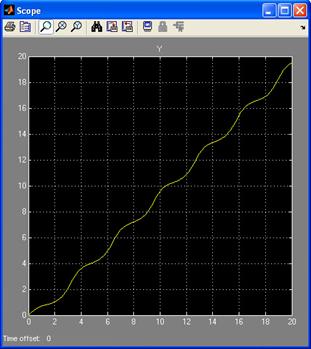
Результатом будет график x от y :
Рассмотрим из каких библиотек взяты использованные блоки.
Ramp – из Sources. Формирует линейный сигнал . В параметрах необходимо задать 1.
Add – Math Operations. В параметрах выбираем необходимые нам операции.
Gain – Math Operations . Коэффициент усиления сигнала. В параметрах ставим значение 3/2.
Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.
Integrator – Continuous . Выполняет интегрирование входного сигнала.
Scope – Sinks . Выводим результат – график сигнала в функции времени.
Дифференциальные уравнения 2-го порядка.
Дана система уравнений:
Решим ее с помощью программы Simulink пакета MATLAB.
Решаем аналогично предыдущему случаю.
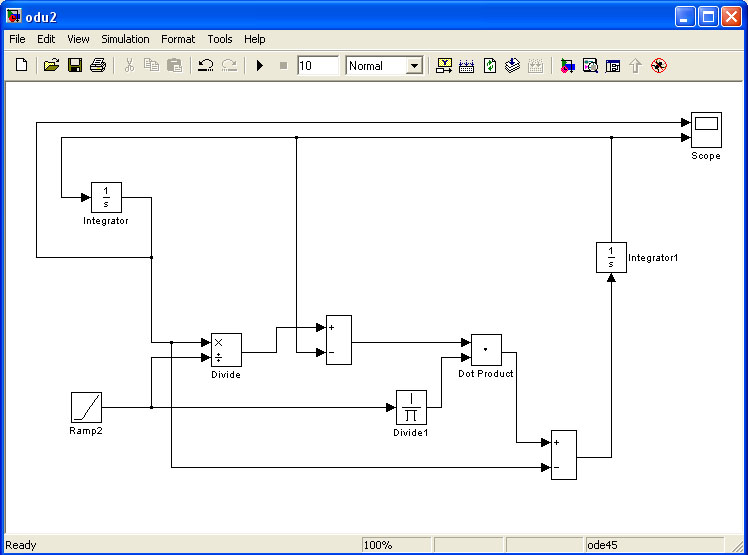
В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x . Обязательно надо в интеграторах задать начальные значения y1(0) = 0.1; y2(0) = 0.5.
Результатом будут два графика:
Рассмотрим из каких библиотек взяты использованные блоки.
Ramp – из Sources . Формирует линейный сигнал. В параметрах необходимо задать все значения 1.
Integrator – Continuous . Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y 1 0.1, для y 2 0.5.
Add – Math Operations . В параметрах выбираем необходимые нам операции.
Divide — Math Operations . Деление первой входной величины на вторую.
Dot Product — Math Operations. Перемножение .
Scope – Sinks. Выводим результат – график сигнала в функции времени.
🌟 Видео
ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Решение систем диф уравнений 1 порядка в среде SimulinkСкачать

Решение_дифференциальных_уравнений_1_порядка_в_Matlab.wmvСкачать

Комментарии к лабораторной работе 1 по моделированию в среде SimulinkСкачать

Моделирование на основе дифференциальных уравненийСкачать

MatLab\Simulink Моделирование RLC-цепиСкачать

ТАУ. Matlab/Simulink - моделирование передаточной функции, снятие характеристикСкачать
Интегрирование систем дифференциальных уравнений. Механический объект. MATLAB, Simulink, Arduino.Скачать

Моделирование механических систем в SimulinkСкачать

Обучение в MATLAB и Simulink: от уравнения к фундаментальным принципамСкачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

1-4 Simulink - Математический маятникСкачать

19) Визуальное моделирование динамических систем в среде MATLAB‐Simulink Часть 1Скачать

Моделирование гидравлических систем в SimulinkСкачать

GMP – 3. Основы MATLAB SimulinkСкачать


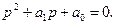
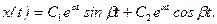
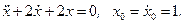
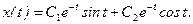
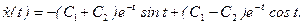
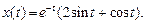
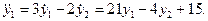
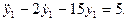
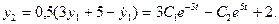
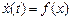 , сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.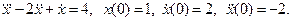
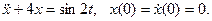
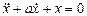 имеет вид:
имеет вид: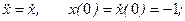
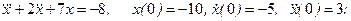
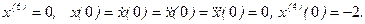
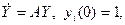 если матрица A имеет вид
если матрица A имеет вид