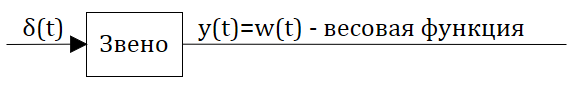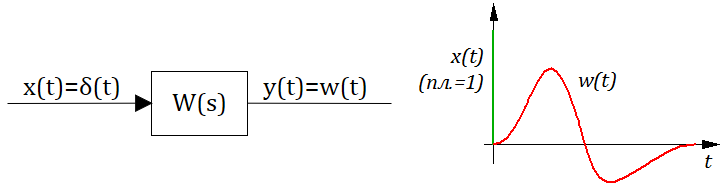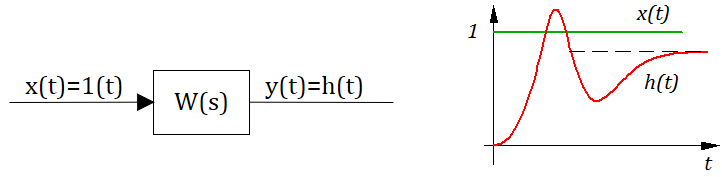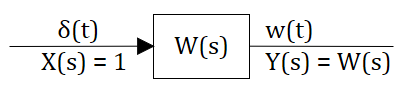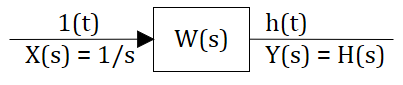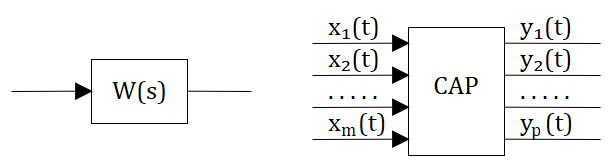Модели вход выход дифференциальные уравнения

Видео:3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать

Электронный учебник по ТАУ (теория автоматического управления)

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

ТАУ ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ: Модели «вход-выход»

Видео:Дифференциальные уравнения. 11 класс.Скачать

1) Дифференциальные уравнения типовых звеньев и систем

Постановка задачи математического описания линейной САУ

Понятие динамического звена

Дифференциальное уравнение динамического звена

В общем случае ДЗ описывают следующим ОДУ

где x(t) и y(t) – входная и выходная величины ДЗ;

a 2 – a 0 ; b 1 – b 0 – коэффициенты (постоянные) уравнения.

Более употребительны в ТАУ иные формы записи этого ДУ. Обычно уравнение (2.1) записывают в символическом виде

Для решения типовых задач ТАУ дифференциальное уравнение ДЗ (2.1) преобразуют по Лапласу (или Карсону-Хевисайду) заменой оператора дифференцирования p комплексной величиной преобразования Лапласа s = j w . Целью названного преобразования является замена операций дифференцирования и интегрирования оригиналов функций y(t) и x(t) алгебраическими действиями над их изображениями Y(s) и X(s), поскольку уравнение (2.1) преобразуется в алгебраическое

При нулевых начальных условиях p º s.

Если свободные члены a 0 = 1 и b 0 = 1, уравнение (2.3) приобретает нормированный вид .

Такую форму записи ДЗ или САУ называют первой стандартной символической (операторной) формой записи. Уравнения (2.1) — (2.4) относят к уравнениям типа «вход — выход«.

Дифференциальное уравнение САУ

В общем случае замкнутую САУ описывают неоднородным ДУ n-го порядка:

где x(t) – входная (управляющая или возмущаю­щая) величина;

y(t) – выходная (управляемая) величина;

К дифференцирующим звеньям (Д-звено) относят:

– идеальное Д-звено с ПФ

– реальное Д-звено с ПФ .

В таблице 2.1 представлены дифференциальные уравнения и переда­точные функции типовых ДЗ.

Типовые соединения динамических звеньев

Сложные элементы и САУ состоят из нескольких соединенных между собой звеньев. Наиболее простыми и часто встречающимися (типовыми) соединениями звеньев являются:

– встречно-параллельное (охват звена обратной связью).

При последовательном соединении ДЗ (рисунок 2.4) выходная величина каждого из звеньев y 1 и y 2 , кроме последнего звена, является входной величиной последующего звена.

Эквивалентная передаточная функция последовательно соединенных l звеньев равна произведению ПФ этих звеньев: .

При параллельном соединении (рисунок 2.5) на вход всех звеньев поступает одна и та же входная величина x(t), а их выходные величины y 1 , y 2 и y 3 суммируются.

Эквивалентная передаточная функ­ция параллельно соединенных l звеньев равна сумме их ПФ:

Третье типовое соединение (рисунок 2.6), называемое встречно-параллельным, приводит к образованию замкнутой системы и состоит из двух звеньев. Звено с ПФ W п (s) образует прямую цепь (связь) передачи сигналов, а звено с ПФ W ос (s) осуществляет ОС.

Эквивалентная ПФ встречно-параллельного соединения звеньев определяется по формуле замыкания

В выражении (2.29) знак «+» соответствует отрицательной ОС, а знак «–» соответствует положительной ОС.

Структурная схема одноконтурной САУ

Алгоритмической структурной схемой САУ называют графическое представление ММ системы в соединении ДЗ, в котором каждой математической операции преобразования сигнала соответствует типовое звено, условно обозначаемое прямоугольником с указанием входных и выходных величин, а так же ПФ этого ДЗ.

Структурная схема типовой одноконтурной САУ показана на рисунке 2.7. На рисунке 2.8 изображена эквивалентная схема типовой САУ.

Очевидно, что эквивалентная схема проще, так как содержит меньше звеньев. Подобного упрощения достигают методом свертки (сущность метода см. п. 2.1.2.6). ПФ звеньев обеих схем связаны согласно (2.27) простейшим образом:

Структурная схема показывает строение САУ, наличие внешних воздействий и точки их приложения, пути распространения воздействий и выходную величину. По существу, структурная схема представляет собой графическую форму ММ САУ, что придает ей наглядность в изображении связей между ДЗ. Это позволяет легко находить по структурной схеме ПФ относительно любых входов и выходов. Для составления структурной схемы САУ необходимо иметь ее функциональную схему (см. п. 1.4) и дифференциальные уравнения или ПФ всех элементов системы.

Передаточные функции САУ

Структурная схема любой одноконтурной САР с любым количеством последовательно или параллельно соединенных звеньев, охваченных местными ОС, может быть сведена к типовой структурной схеме, показанной на рисунке 2.8. Основную ПФ, связывающую изображение выходной величины Y ( s ) с изображением задающего воздействия G ( s ), обозначают Ф( s ): ,

Для следящих систем характерно равенство W yg (s) = W(s). Структурная схема таких САУ показана на рисунке 2.9, а саму САУ называют системой с единичной ОС.

Основная ПФ названной САУ имеет вид .

Таким образом, основная ПФ Ф( s ) определяется по ПФ разомкнутой системы W(s).

Основная ПФ системы Ф(s) характе­ризует передачу САУ задающего воздействия g(t), его воспроизведение управляемой величиной y (t). Воспроизве­дение тем лучше, чем ближе Ф(s) к идеальному значению

ПФ разомкнутой САУ определяют по преобразованной структурной схеме САУ (рисунок 2.10). При этом контур регулирования полагают разомкнутым около сумматора и считают все возмущающие воздействия равными нулю (z = 0). ПФ разомкнутой типовой САУ определяется по формуле (2.27):

ПФ разомкнутой САУ W(s) характеризует соб­ственные динамические свойства САУ и позволяет определить ее устойчивость, а так же выбрать коррек­тирующее устройство для улучшения свойств САУ.

В общем случае ПФ разомкнутой САУ представляет собой дробно-рациональную функцию оператора s:

Реальные САУ всегда имеют m . Многочлен A(s) называют характеристическим полиномом разомкнутой САУ, а уравнение A(s) = 0 представляет собой характеристическое уравнение разомкнутой САУ

ПФ разомкнутой САУ обычно записывают в стандартной форме, при которой полиномы B(s) и A(s) имеют свободные члены и , т.е.

Величину v называют порядком астатизма САУ относительно задающего воздействия g(t).

Статические САУ характеризуются v = 0 и имеют ПФ вида .

Астатические САУ характеризуются астатизмом v ¹ 0. В случае v = 1 разомкнутая система имеет ПФ вида

так как свободный член полинома знаменателя A(s) равен нулю (a 0 = 0). Замкнутую САУ при этом называют астатической САУ первого порядка. Такая система содержит в прямой цепи одно И-звено. САУ с двумя И‑звеньями (v = 2) называют астатической САУ второго порядка.

Для определения влияния возмущения z(t) на управляемую величину y (t) структурную схему типовой САУ (рисунок 2.8) следует представить в виде, показанном на рисунке 2.11.

При этом звено с ПФ W 2 ( s ) образует собой прямую цепь, звенья с ПФ W 1 ( s ) и W 3 ( s ) – обратную связь. Тогда в соответствии с (2.29) ПФ замкнутой САУ по возмущению

что позволяет «свернуть» структурную схему САУ (рисунок 2.12) и изобразить САУ звеном с эквивалентной ПФ (2.40).

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

F z ( s )

ПФ F z ( s ) показывает влияние возмущения z(t) на управляемую величину y (t). Возмущение отклоняет её от заданного значения g (t) и уменьшает точность воспроизведения задающего воздействия. Это отрицательное влияние возмущения тем меньше, чем ближе F z ( s ) к идеальному значению F z ( s ) = 0.

При одновременном приложении к линейной САУ управляющего g(t) и возмущающего z(t) воздействий в соответствии с принципом наложения изображение регулируемой величины определяется следующим образом:

При исследовании САУ часто интересуются значением ошибки регулирования (1.1):

ПФ замкнутой САУ по ошибке определяется по следующей формуле:

Структурная схема системы с ПФ F e ( s ) вида (2.41) показана на рисунке 2.13. При этом считают, все внешние воздействия z(t) = 0, исключая задающее воздействие g (t).

Передаточная функция F e ( s ), как и F ( s ), характеризует воспроизведение управляемой величиной y (t) задающего воздействия g (t) (отработку задания). Воспроизведение тем лучше, чем ближе F e ( s ) к идеальному значению F e ( s ) = 0.

ПФ САУ по ошибке (2.41) позволяет рассчитать значение статической ошибки системы по следующей формуле:

Часто статическую ошибку принимают за оценку точности статической САУ.

Эквивалентные преобразования структурных схем

Структурную схему любой сложности путем последовательных преобразований можно привести к эквивалентной одноконтурной (рисунок 2.14). Условием эквивалентности является сохранение в процессе преобразований зависимости основных величин y(t), e (t) и y ос (t) от внешних воздействий z (t).

Эквивалентные преобразования структурных схем осуществляют по соответствующим правилам в следующей последовательности. Прежде всего каждое имеющееся в схеме типовое соединение звенев заменяют эквивалентным звеном. Затем целесообразно выполнить перенос точек разветвления (узлов) в соответствии с рисунком 2.15 и сумматоров в соответствии с рисунком 2.16, чтобы в преобразованной таким образом схеме образовались новые типовые соединения звеньев. Эти соединения опять должны быть заменены эквивалентными звеньями. Узел может быть перенесен назад через звено W 1 ( s ) или вперед через звено W 2 ( s ). В первом случае в ответвление включают звено с ПФ W 1 ( s ), во втором – звено с ПФ 1/ W 2 ( s ). Подобным образом поступают при переносе сумматора.

Таким образом, указанные правила позволяют преобразовать сложные структурные схемы многоконтурных САУ с перекрещивающимися связями, а также с несколькими входами и выходами. Преобразование структурных схем позволяет определить ПФ САУ любой сложности.

Типовые воздействия

Работа многих САУ сопровождается резкими изменениями внешних воздействий (например, уменьшением или увеличением нагрузки и т.п.). Важно оценить поведение САУ в таких ситуациях, т.е. выяснить, насколько значительным будет отклонение от нормального режима работы и насколько быстро и точно оно будет устранено регулятором. Для того, чтобы сравнить поведение при этом различных САУ и элементов, рассматривают строго определенное, нормированное, изменение воздействий. Таким типовым изменением воздействия считают мгновенное его изменение от нуля до единицы. Для математической записи используют единичную ступенчатую функцию (функцию Хевисайда):

Другим часто встречающимся изменением внешних воздействий являются их кратковременные, но значимые всплески, импульсы. Например, ударная нагрузка на двигатель, порывы ветра, действующие на летательный аппарат и т.п. Нормированным (стандартным) импульсным воздействием счи­тают единичный импульс, т.е. импульс, произведение длитель­ности которого на его ампли­туду равно единице.

Предел, к которому стре­мится единичный импульс, когда его продолжительность стремится к нулю T ® 0, есть единичная импульсная функция ( d -функция или функция Дирака):

Приблизительно d -функцию можно представить как очень узкий прямоугольный импульс длительности T и амплитуды около начала координат (рисунок 2.18), так что его площадь (интеграл) равна единице: .

Это равенство описывает основное свойство d -функции. Кроме того, считают, что d -функция равна первой производной единичной ступенчатой функции

Рассмотренные воздействия относят к динамическим, так как с их помощью анализируют динамические свойства САУ (см. п. 2.14).

Свойства элементов и САУ оценивают также в установившихся режимах. Для этого к системе или элементу прикладывают периодическое воздействие. Наиболее часто используют гармоническое воздействие вида

Такой выбор обусловлен тем, что любое реальное периодическое воздействие может быть представлено рядом гармонических составляющих (рядом Фурье): .

Реакцию линейной САУ на реальное воздействие определяют методом наложения (суперпозиции).

Временн Ï е характеристики динамических звеньев и САУ

К временн Ï м (динамическим) характеристикам САР относят переходную и импульсную характеристики.

Переходной характеристикой (функцией) h(t) называют функцию, описывающую аналитически или графически изменение выходной величины звена или САУ y(t), вызванное единичным ступенчатым воздействием x ( t ) = 1( t ) на входе звена или САУ при нулевых начальных условиях. Другими словами h(t) есть реакция звена или САУ на единичное ступенчатое воздействие при нулевых начальных условиях. Переходные характеристики и функции типовых ДЗ представлены в таблице 2.2.

Импульсной характеристикой (функцией) или весовой характеристикой звена или САУ w(t) называют характеристику, описывающую реакцию ДЗ или САУ на единичное импульсное воздействие на входе звена или САУ при нулевых начальных условиях. Импульсные характеристики и функции типовых ДЗ представлены в таблице 2.3

Видео:Модели на основе дифференциальных уравнений с запаздыванием.Скачать

Частотные характеристики

В тех случаях, когда протекающие процессы в САУ изучены слабо, и вывод ДУ, описывающих эти САУ, затруднен, в основу математического моделирования кладут не уравнения движения, а так называемые частотные характеристики (ЧХ) систем.

Частотные характеристики динамических звеньев

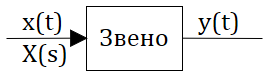
Если на вход стационарного ДЗ (рисунок 2.1) действует гармонический сигнал то на выходе ДЗ установится также гармонической сигнал той же угловой частоты w , но с измененными амплитудой Y m и начальной фазой y 2 (рисунок 2.19). Эти изменения зависят как от свойств самого ДЗ, так и от угловой частоты входного воздействия.

Отношение амплитуд выходного и входного сигналов

разность их фаз

j ( w ) = y 2 — y 1

являются функциями частоты. Их называют соответственно амплитудно-частотной характеристикой (АЧХ) и фазово-частотной характерис­тикой (ФЧХ) звена.

Эти характеристики показывают, что линейное ДЗ изменяет амплитуду и фазу гармонического сигнала: в установившемся режиме амплитуда уменьшается или увеличивается в A раз, а фазовый сдвиг уменьшается или увеличивается на j градусов (радиан) при изменении угловой частоты w . Частотные характеристики зависят от свойств ДЗ, но не зависят от амплитуды и фазы входного воздействия. АЧХ может служить для оценки фильтрующих свойств, а ФЧХ – инерционных свойств ДЗ.

Частотные характеристики всякого элемента САУ связаны с его ПФ W ( s ). Подставляя в выражение ПФ вместо оператора Лапласа s мнимую величину j w , получают комплексную функцию частоты W(j w ), которую называют частотной передаточной функцией. Эта функция при любой частоте w является комплексной величиной и поэтому может быть представлена в показательном виде

Следовательно, модуль и аргумент частотной ПФ определяют соответственно АЧХ и ФЧХ звена.

Частотная ПФ, как комплексная функция, может быть также представлена и в алгебраическом виде

где U ( w ); V ( w ) – функции частоты, называемые соответственно вещественной (действительной) и мнимой ЧХ.

Они не имеют конкретного физического смысла, но используются в расчетах и определяются по формулам:

Частотные характеристики связаны между собой известными соотношениями (рисунок 2.20):

Если частотная ПФ задана в алгебраи­ческом виде (2.55), преобразование ее к показательному виду (2.52) осуществляют по формулам (2.58). Соотношения (2.59) позволяют осуществить при необходимости обратное преобразование.

Кроме аналитического описания ЧХ изображают графически в декартовых координатах. Построение АЧХ и ФЧХ осуществляют по формулам (2.53) и (2.54). На рисунках 2.21 и 2.22 изображены в самом общем виде соответственно АЧХ и ФЧХ обыкновенных инерционных ДЗ или САУ. В таблице 2.4 приведены АЧХ и ФЧХ типовых ДЗ.

К обычным ЧХ относят ампли­тудно-фазовую частотную характе­ристику (АФЧХ). АФЧХ представляет собой годограф частотной ПФ W(j w ), т.е. геометрическое место концов вектора W(j w ) при изменении частоты w от 0 до ± ¥ . Эту характеристику строят на комплексной плоскости в полярных ( A , w ) или декартовых ( U , V ) координатах конца вектора W(j w ) по формулам (2.52), (2.53) или (2.55), (2.56).

Типичный годограф W(j w ) обыкно­венного инерционного ДЗ показан на рисунке 2.20 в диапазоне частот — ¥ w + ¥ . Рабочая ветвь годографа соответствует физически реализуемым положительным частотам w ³ 0. Фазовые углы j ( w ) отсчитывают от положительной действительной полуоси (+1) против движения часовой стрелки. Инерционные звенья характеризуются отрицательными фазовыми углами j ( w ) Логарифмические частотные характеристики

Логарифмические амплитудно-частотная (ЛАЧХ) и фазово-частотная (ЛФЧХ) характеристики удобны тем, что небольшим графиком может быть охвачен широкий диапазон частот. При этом одинаково наглядно изменение частотных свойств как на малых, так на средних и высоких частотах.

Небольшим графиком охватывается и широкий диапазон изменения амплитуды при одинаковой наглядности изменения больших и малых амплитуд.

В качестве примера на рисунках 2.23 и 2.24 показаны АЧХ одного и того же А-звена первого порядка (k = 1 и T = 10) в диапазонах частот, отличающихся только на один порядок. По второму графику практически не возможно судить о свойствах исследуемого ДЗ в области малых частот w

Для сравнения на рисунке 2.25 изображена ЛАЧХ указанного А-звена в диапазоне частот 0 w 4. Очевидно, что ЧХ, построенная в логарифмических координатах, точно передает характер исследуемой зависимости на всех частотах. Кроме того, значительные непрямолинейные участки ЛАЧХ с большой точностью могут быть заменены прямыми линиями – асимптотами. В этом случае ЛАЧХ изображают отрезками прямых (асимптот) и называют асимптотической или приближенной ЛАЧХ (рисунок 2.26).

Асимптоты имеют отрицательный и положительный наклон, кратный 20 дБ на декаду. Для построения асимптотической ЛАЧХ проводят простые вычисления, так как любую асимптоту можно построить по двум точкам. При построении ЛАЧХ (рисунок 2.25) по оси абсцисс откладывают частоту в логарифмическом масштабе, т.е. наносят отметки, соответствующие lg W , где – относительная частота. Однако около этих отметок указывают частоты w . Отрезок оси абсцисс, соответствующий изменению частоты в 10 раз, называют декадой ( ), а отрезок, соответствующий изменению частоты в два раза, – октавой ( ). Декада и октава – равномерные единицы на оси абсцисс. Нуль оси обсцисс лежит слева в бесконечности, так как lg0 = — ¥ . Поэтому при построении ЛАЧХ выбирают такой отрезок оси абсцисс, который охватывает требуемый диапазон частот ( w 1 , w 2 ), например, полосу пропускания (0, w п ). В качестве «базовой» частоты w 2 удобно в этом случае принять частоту среза, т.е. w 2 = w ср (рисунок 2.21). По оси ординат ЛАЧХ откладывают в равномерном масштабе в децибеллах (дБ) логарифми­ческую амплитуду

Децибелл является единицей логарифмической относительной величины. Изменение отношения двух амплитуд в 10 раз ( ) соответствует изменению усиления на 20 дБ (см. таблицу 2.5).

ЛФЧХ имеет такую же ось абсцисс, что и ЛАЧХ. По оси ординат ЛФЧХ откладывают в равномерном масштабе угол фазового сдвига j . Оси абсцисс ЛФЧХ и ЛАЧХ обычно совмещают, чтобы изменения фазы можно было сопоставлять с изменениями амплитуды.

Точные и приближенные (асимптотические) ЛАЧХ типовых ДЗ приведены в таблице 2.6.

В англоязычной технической литературе и современных математических системах (M A TLAB, Maple и др.) ЛАЧХ и ЛФЧХ называют диаграммами Боде ( Bode diagramms ).

Понятие об идентификации

Идентификацией динамической системы называют получение или уточнение по экспериментальным данным ММ этой системы. ММ может быть выражена ДУ, ПФ и т.п. Получение ММ в таком виде составляет задачу непараметрической идентификации. Параметры модели являются результатом параметрической идентификации.

Классическими методами непараметрической идентификации линей­ных САУ или ее элементов являются:

– метод временн Ï х характеристик;

– метод частотных характеристик;

– метод корреляционных функций.

К прямым методам параметрической идентификации относят:

– метод наименьших квадратов;

– метод сумм произведений и др.

Выбор того или иного метода идентификации и оценки параметров ММ зависит от априорной информации об объекте исследования и требованиях, предъявляемых к ММ. На практике чаще используют метод временн Ï х характеристик как более простой в организации эксперимента. Если эксперимент проводят для получения переходной характеристики h(t), метод называют методом переходных характеристик (функций). Традиционно объединяют метод переходных характеристик с регрессионным анализом, основу которого составляет метод наименьших квадратов (МНК). Созданная таким образом ММ является регрессионной моделью, качество которой гарантированно статистически.

Сущность метода переходных характеристик заключается в следующем. До начала эксперимента изучают объект идентификации и разрабатывают программу его исследования, а также оценивают возможность считать объект линейным, стационарным, с сосредоточенными параметрами. Названные допущения позволяют описать динамические свойства исследуемого объекта ОДУ (2.5) или ПФ. Если объектом идентификации является элемент САУ, то по его физическим свойствам предварительно выбирают ММ из числа типовых ДЗ (см. п. 2.1.2.2). Затем проводят активный эксперимент. Для этого сначала приводят исследуемый объект в исходное установившееся состояние. После этого ступенчато изменяют входное воздействие на D x и регистрируют соответствующее изменение во времени выходной величины D y = f ( t ). Эту зависимость называют разгонной характеристикой (см. п. 3.2) и обозначают y ( t ). По достижении объектом нового установившегося состояния прекращают эксперимент. Полученную экспериментально разгонную характеристику y ( t ) аппроксимируют теоретической переходной функцией h ( t ). Эта функция является решением ОДУ, принятого в качестве ММ объекта идентификации. Аппроксимирующую переходную функцию h ( t ) выбирают первоначально из переходных функций типовых ДЗ (см. таблицу 2.2) при условии наибольшего соответствия характеристик y ( t ) и h ( t ) друг другу. Типовое ДЗ, переходная функция которого выбрана в качестве аппроксимирующей, таким образом, принимается в качестве ММ исследуемого объекта. Определяется порядок ОДУ, решением которого является аппроксимирующая характеристика h ( t ). Уравнение характеристики h ( t ) записывают в явном виде (см. таблицу 2.1). В этом уравнении неизвестными остаются только коэффициенты. Их находят решением обратной задачи: по известным значениям функции h ( t ) и соответствующим им значениям аргумента (времени t ) рассчитывают неизвестные коэффициенты. Эта задача является оптимизационной в том смысле, что искомые коэффициенты должны обеспечить минимум расхождения между характеристиками h ( t ) и y ( t ). В качестве критерия расхождения чаще всего принимают минимум суммы квадратов ошибок по всей совокупности измерений (принцип Лежандра):

Этот метод называют методом наименьших квадратов (МНК). С его помощью строят уравнение регрессии h ( t ), которым аппроксимируют разгонную характеристику y ( t ). Идентификация будет полной, если будет доказана адекватность принятой ММ. Названную модель считают адекватной, если расхождение между характеристиками h ( t ) и y ( t ) является незначительным в статистическом смысле. Оценку адекватности уравнения регрессии в целом проводят по F -критерию Фишера. При положительном результате проверки уравнения регрессии оценивают значимость его коэффициентов по t -критерию Стьюдента. Одновременно коэффициенты уравнения регрессии являются коэффициентами ММ.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

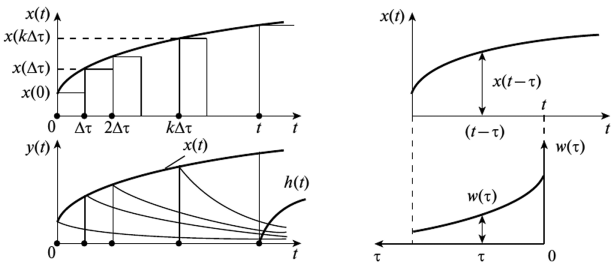
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

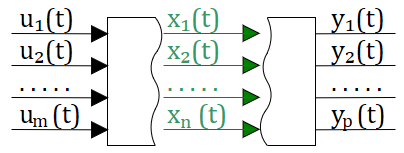
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
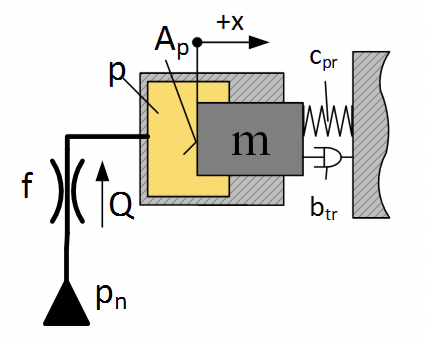
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

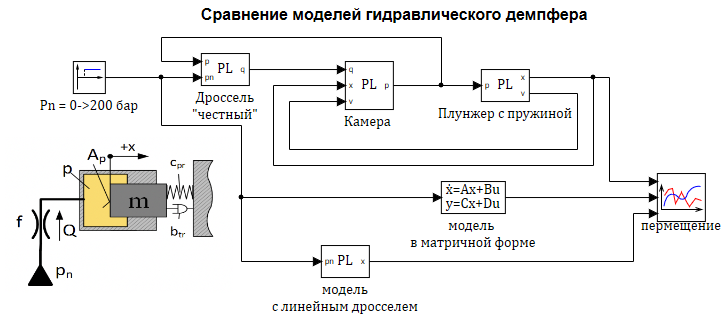
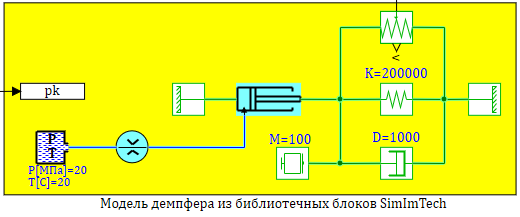
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

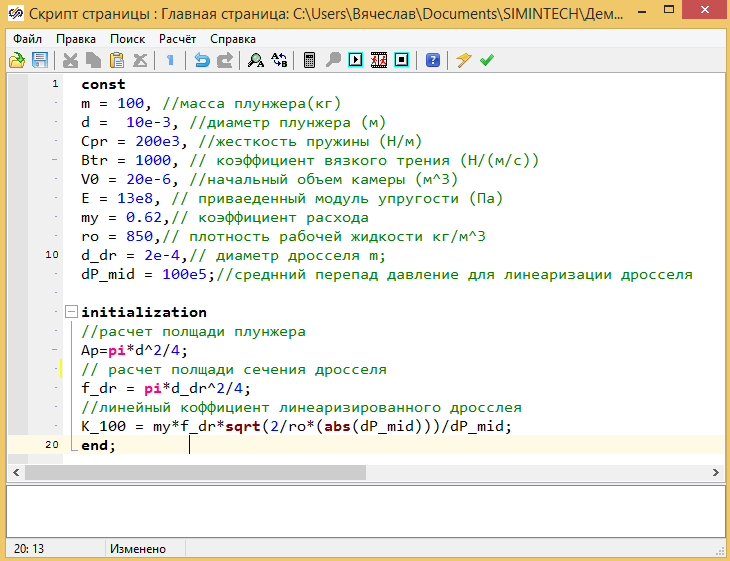
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

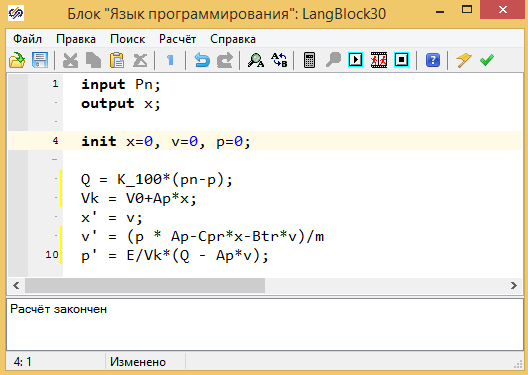
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

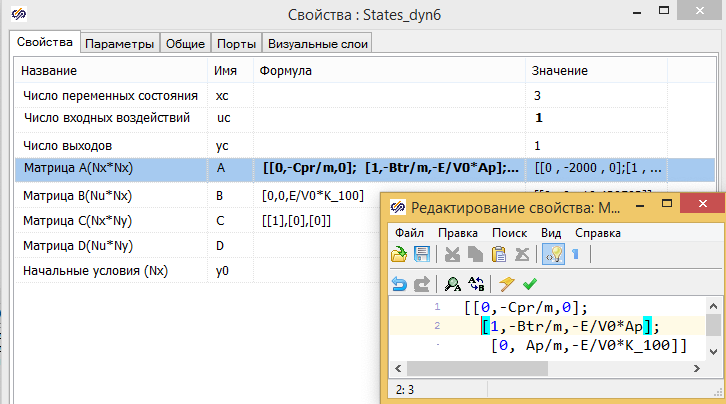
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

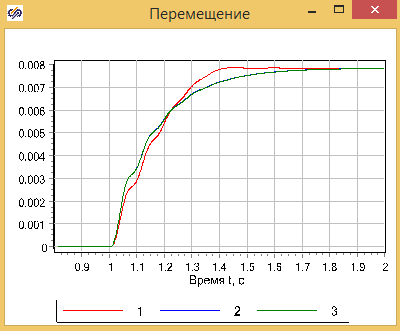
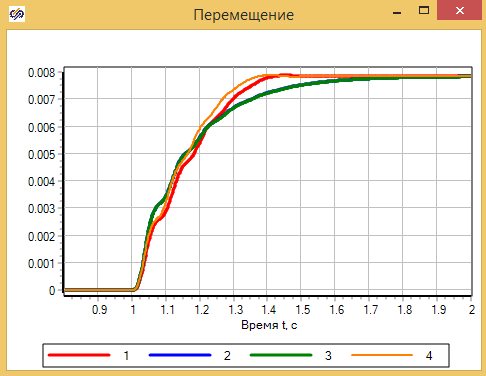
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

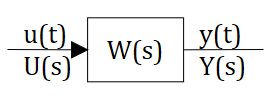
Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

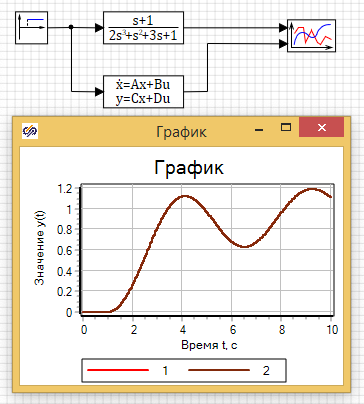
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Energy
education

сайт для тех, кто хочет изучать энергетику

Метрология и автоматизация

Система управления

Система управления — строго определённый набор средств сбора сведений о подконтрольном объекте и средств воздействия на его поведение, предназначенный для достижения определённых целей. Объектом системы управления могут быть как технические объекты, так и люди.

3. Модели линейных объектов

Дифференциальные уравнения

Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка.

Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта – напряжение якоря $u(t)$ (в вольтах), выход – угол поворота вала $θ(t)$ (в радианах).

Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения $ω(t)$ (в радианах в секунду) остается постоянной, при этом угол $θ(t)$ равномерно увеличивается.

Чем больше напряжение, тем быстрее вращается вал. Если подключить нагрузку, например, заставить двигатель вращать турбину, скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.

Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения $ω(t)$ вычисляется как производная от угла поворота вала $θ(t)$, то есть

Соответственно, угол $θ(t)$ – это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде

где $M(t)$ – вращающий момент (измеряется в H·м), $M_н (t)$ – момент нагрузки (возмущение, также в H·м). Буквой $J$ обозначен суммарный момент инерции якоря и нагрузки (в кг·м 2 ). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).

Перейдем к электротехнике. В нашем случае момент $M(t)$ – это электромагнитный момент двигателя, который вычисляется по формуле

где $C_м$ – коэффициент, $Ф$ – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); $i(t)$ – ток якоря (в амперах), который может быть найден из уравнения

где $e(t)$ – электродвижущая сила (ЭДС) якоря (в вольтах) и $R$ – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения:

где $C_ω$ – коэффициент. Вводя новые постоянные $k_1=C_м·Ф$ и $k_2=C_ω·Ф$, можно записать модель двигателя в виде системы уравнений

Модель описывает связи реальных сигналов в системе, ее внутреннее устройство.

Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Переходя к переменной $θ(t)$, получаем:

или, перенося все члены, зависящие от $θ(t)$, в левую часть равенства

Это дифференциальное уравнение второго порядка, связывающее вход $u(t)$ и нагрузку $M_н (t)$ с выходом $θ(t)$. В сравнении с системой, все внутренние сигналы исходной модели $e(t)$ и $i(t)$ были исключены из уравнений. Поэтому последнее уравнение называется уравнением «вход-выход».

Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.

В этом разделе на простом примере рассмотрено, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения.

Модели в пространстве состояний

Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.

Рассмотрим снова модель электродвигателя, считая, что $M_н (t)=0$ (нагрузки нет). Вспомнив, что $ω(t)=frac<mathrmθ(t)><mathrmt>$, можно записать

Эта система дифференциальных уравнений первого порядка быть записана в матричной форме:

Значения $θ(t)$ и $ω(t)$ определяют состояние двигателя в момент времени $t$. Это значит, что зная их значения в некоторый момент времени $t_0$ и входной сигнал $u(t)$ при всех $t≥t_0$ можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения $θ(t)$, $ω(t)$ и $u(t)$ (при $t 0$ дает возможность однозначно определить дальнейшее поведение этого объекта.

Первое уравнение в системе позволяет найти производную, то есть, скорость изменения вектора состояния $x(t)$ в любой момент времени. Будем считать, что при $0≤t≤∆t$, где $∆t$ – малый интервал времени, эта производная не меняется. Тогда значение вектора состояния при $t=∆t$ приближенно определяется формулой

то есть, его можно легко вычислить. Зная $x(∆t)$ и сигнал управления $u(∆t)$, находим выход системы в тот же момент

Эту методику можно применять и дальше, в конце второго интервала получаем

Таким образом, можно (приближенно) рассчитать выход системы при всех $t>0$. Конечно, точность будет тем выше, чем меньше $∆t$, однако объем вычислений при этом также увеличится.

Этот метод приближенного решения дифференциальных уравнения называется методом Эйлера.

Передаточная функция

Выходной сигнал системы можно представить как результат действия некоторого оператора на ее вход. Для линейных моделей такой оператор можно записать следующим образом.

Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход $x(t)$ и выход $y(t)$:

где $a_i (i=0,1)$ и $b_i (i=0,1,2)$ – постоянные. Введем оператор дифференцирования $p=frac<mathrm><mathrmt>$, который действует на сигнал $x(t)$ по правилу $p x(t)=frac<mathrmx(t)><mathrmt>$. Обратите внимание, что запись $p x(t)$ обозначает не умножение оператора $p$ на $x(t)$, а действие этого оператора, то есть дифференцирование $x(t)$.

Теперь запишем производные сигналов $x(t)$ и $y(t)$ по времени в операторной форме

Подставляя эти выражения, получим

$$b_2 p^2 y(t)+b_1 p y(t)+b_0 y(t)=a_1 p x(t)+a_0 x(t).$$

Можно формально вынести за скобки $y(t)$ в левой части равенства и $x(t)$ в правой части:

$$(b_2 p^2+b_1 p+b_0 )y(t)=(a_1 p+a_0 )x(t).$$

Левая часть означает, что оператор $b_2 p^2+b_1 p+b_0$ действует на сигнал $y(t)$, а в правой части оператор $a_1 p+a_0$ действует на сигнал $x(t)$. «Разделив» (условно, конечно) обе части на оператор $b_2 p^2+b_1 p+b_0$, связь выхода и входа можно записать в виде

где запись $W(p)·x(t)$ означает не умножение, а действие сложного оператора

на сигнал $x(t)$. Иначе говоря, формула $y(t)=W(p)·x(t)$ – это не что иное, как символическая запись, которую удобно использовать.

Функция $W(p)$ называется передаточной функцией объекта. Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.

Часто передаточной функцией называют функцию $W(λ)$, которая получается в результате замены оператора $p$ на некоторую независимую переменную $λ$. Эта фукнция представляет собой отношение двух полиномов (многочленов) от $λ$.

Передаточная функция $W(λ)$ называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Например, функция $frac$ – строго правильная и одновременно правильная; $frac$ – правильная, но не строго правильная (иногда такие функции называют биправильными), а $frac$ – неправильная.

Нулями передаточной функции называются корни ее числителя, а полюсами – корни знаменателя. Например, функция

имеет нуль в точке $λ=1$ и два полюса в точках $λ=-1$ и $λ=-2$.

Преобразование Лапласа

Одна из первых задач, которые были поставлены в теории управления – вычисление выхода системы при известном входе. Мы видели, что для ее решения нужно решать дифференциальные уравнения. Чтобы упростить процедуру, математики придумали преобразование, которое позволило заменить решение дифференциальных уравнений алгебраическими вычислениями, то есть, операциями с полиномами (многочленами) и рациональными функциями.

Для функции $f(t)$ вводится преобразование Лапласа, которое обозначается как $mathscr$:

Функция $F(s)$ называется изображением для функции $f(t)$ (оригинала). Здесь $s$ – это комплексная переменная, которая выбирается так, чтобы интеграл сходился.

Обратное преобразование Лапласа $mathscr^ $ позволяет вычислить оригинал $f(t)$ по известному изображению $F(s)$:

где $j=sqrt$, а постоянная σ выбирается так, чтобы интеграл сходился.

На практике вместо интеграла чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот. Например, изображения по Лапласу для дельта-функции, единичного скачка и функции $e^$ равны, соответственно

Преобразование Лапласа имеет несколько замечательных свойств. Во-первых, легко доказать, что принцип суперпозиции выполняется как для прямого, так и для обратного преобразования Лапласа:

Во-вторых, изображение для производной функции $f(t)$ равно

где $F(s)$ – изображение функции $f(t)$, и $f(0)$ – ее значение при $t=0$. Поэтому при нулевых начальных условиях изображение производной равно изображению самой функции, умноженному на $s$. Аналогично для построения изображения i-ой производной нужно умножить изображение функции на $s^i$ (это также справедливо только при нулевых начальных условиях).

Кроме того, с помощью преобразование Лапласа можно сразу найти начальное и конечное значения функции-оригинала (при $t=0$ и $t→∞$), не вычисляя самого оригинала:

Рассмотрим снова уравнение

Применим к левой и правой частям преобразование Лапласа, считая, что все начальные условия нулевые. Получается уравнение в изображениях, связывающее преобразования Лапласа входа $X(s)$ и выхода $Y(s)$:

$$b_2 s^2 Y(s)+b_1 sY(s)+b_0 Y(s)=a_1 sX(s)+a_0 X(s).$$

Можно вынести за скобки $Y(s)$ в левой части и $X(s)$ в правой части:

$$(b_2 s^2+b_1 s+b_0 )Y(s)=(a_1 s+a_0 )X(s).$$

Разделив обе части этого равенства на $b_2 s^2+b_1 s+b_0$, получаем

$$Y(s)=(a_1 s+a_0)/(b_2 s^2+b_1 s+b_0 ) X(s)=W(s)·X(s).$$

$W(s)$ – это передаточная функция объекта, записанная в виде функции от комплексной переменной $s$, а не от оператора дифференцирования $p$.

Таким образом, при нулевых начальных условиях изображение выхода линейного объекта вычисляется как произведение его передаточной функции на изображение входного сигнала.

Из этого следует и другой важный вывод: передаточная функция равна отношению изображений по Лапласу выхода и входа при нулевых начальных условиях.

Рассмотрим пример использования преобразования Лапласа для вычисления выхода системы при известном входном сигнале. Пусть объект управления описывается уравнением первого порядка:

и на его вход поступает единичный ступенчатый сигнал $x(t)=1(t)$. Требуется найти сигнал выхода $y(t)$, который в данном случае представляет собой переходную характеристику.

Решим эту задачу с помощью передаточных функций и изображений сигналов по Лапласу. Чтобы найти изображение выхода, нужно знать изображение входного сигнала $X(s)$ и передаточную функцию звена $W(s)$. Изображения находим по табличным данным, повторяя приведенные выше рассуждения:

Теперь находим изображение выхода

Вычисляем оригинал – сигнал выхода:

Обратное преобразования Лапласа:

$$y(t)=-k·left (expleft (fracright )-1right ).$$

Таким способом можно вычислять реакцию системы на известный входной сигнал без прямого решения дифференциального уравнения.

Вычислим начальное и конечное значение сигнала выхода $y(t)$:

Значение $W(0)$ называют статическим коэффициентом усиления звена, поскольку он показывает, во сколько раз усиливается постоянный сигнал.

Переходная функция

Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент $t=0$. Формально этот сигнал определяется так:

$$1(t)=begin 0,t Реакция объекта на единичный скачок.

При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.

Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.

Пусть модель объекта задана дифференциальным уравнением первого порядка

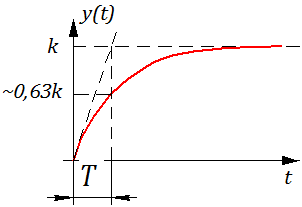
где $k$ – безразмерный коэффициент, а $T$ – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение при $x(t)=1(t)$, получаем

где постоянная $C_1$ должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть $y(0)=0$, что дает $C_1=-k$ и поэтому

На рисунке показаны переходные характеристики модели при различных значениях параметра $T$, который называется постоянной времени звена.

Видно, что при увеличении $T$ выход $y(t)$ медленнее достигает установившегося значения, равного $k$, то есть постоянная времени характеризует инерционность звена. Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.

Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.

Импульсная характеристика (весовая функция)

В качестве тестового сигнала можно, в принципе, использовать любой сигнал. Например, можно изучать реакцию системы на прямоугольный импульс. Вопрос в том, чтобы определить некоторый стандартный вид этого импульса. На рисунке показаны три импульса, имеющих одинаковые площади. Для простоты будем считать, что эта площадь равна единице.

Что будет, если мы будем уменьшать ширину импульса, сохраняя его площадь? Очевидно, что высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Таким образом, мы получили еще один классический тестовый сигнал – единичный импульс или дельта-функцию Дирака $δ(t)$. Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме $t=0$, где он уходит к бесконечность, причем его площадь (интеграл по всей оси времени) равен единице:

Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице.

Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала $1(t)$. Действительно, эта производная равна нулю при всех значениях $t$, кроме нуля, где она обращается в бесконечность.

Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикой и обозначается $w(t)$:

Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.

Рассматривая дельта-функцию как предельный случай прямоугольного сигнала единичной площади, можно найти связь между переходной функцией и импульсной характеристикой.

Пусть ширина прямоугольного импульса равна $ε$, а высота – $frac$ . Такой импульс можно представить в виде разности двух ступенчатых сигналов

где $1(t-ε)$ – это единичный ступенчатый сигнал, который приходит в момент $t=ε$, то есть, смещен по времени на $ε$.

Так как для линейных систем справедлив принцип суперпозиции, сигнал на выходе будет равен разности реакций системы на входы $1(t)$ и $1(t–ε)$, умноженной на коэффициент $frac$. Учитывая, что реакция на сигнал $1(t)$ – это переходная функция $h(t)$, получаем

Переходя к пределу при $ε→0$, находим, что импульсная характеристика

как оказывается, равна производной от переходной функции. Наоборот, переходная функция – это интеграл от импульсной характеристики на интервале от 0 до $t$:

Дифференцируя переходную характеристику звена первого порядка, получаем соответствующую импульсную характеристику:

Другое название импульсной характеристики – весовая функция. Это название связано с тем, что для произвольного входного сигнала $x(t)$ выход системы $y(t)$ при нулевых начальных условиях вычисляется как интеграл

Здесь функция $w(t)$ как бы «взвешивает» входной сигнал $x(t)$ в подынтегральном выражении.

Заметим, что импульсная характеристика дает неполную информацию об объекте, поскольку не учитывает ненулевые начальные условия.

В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы, строго говоря, экспериментально не удается.

Частотные характеристики

Еще один популярный эталонный сигнал – гармонический (синус, косинус), например:

где $ω$ – угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших $t$) будет синус той же частоты, но с другой амплитудой $A$ и сдвигом фазы $φ$:

Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг $φ$, нужно найти расстояние $∆t$ по оси времени между соответствующими точками синусоид (например, точками пересечения с осью $t$ или вершинами). Если $∆t$ умножить на частоту $ω$, получаем сдвиг фазы $φ$ (в радианах).

На рисунке показан случай $φ>0$ (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного.

Зная передаточную функцию системы $W(s)$, можно вычислить амплитуду и сдвиг фазы по формулам

Запись $W(jω)$ означает, что в передаточную функцию $W(s)$ подставляется чисто мнимое число $s=jω$, где $j=sqrt$. Для каждой частоты ω значение $W(jω)=P+jQ$ – это некоторое комплексное число, имеющее амплитуду

Функция $W(jω)$ называется частотной характеристикой звена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости $P(ω)$ и $Q(ω)$ – это вещественная и мнимая частотные характеристики.

Функции $A(ω)$ и $φ(ω)$ называются соответственно амплитудной и фазовой частотными характеристиками (АЧХ и ФЧХ). Амплитудная частотная характеристика – это коэффициент усиления гармонического сигнала. Если на какой-то частоте ω значение $A(ω)>1$, входной сигнал усиливается, если $A(ω) Амплитудные частотные характеристики идеальных фильтров.

В радиотехнике используется понятие полосы пропускания – это ширина полосы частот, в которой значение АЧХ больше, чем $frac<sqrt>$ от ее максимального значения.

Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал и записывается сигнал $y(t)$ на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики.

Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2022. All rights reserved.

📺 Видео

1.1. Составление имитационной модели в виде дифференциального уравненияСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

5) ТАУ для чайников. Часть 3.1: Модели линейных объектов...Скачать

Моделирование на основе дифференциальных уравненийСкачать

Модели, представленный системой двух дифференциальных уравненийСкачать

Модели биологических систем, описываемые одним дифференциальным уравнением первого порядкаСкачать

1. Что такое дифференциальное уравнение?Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать