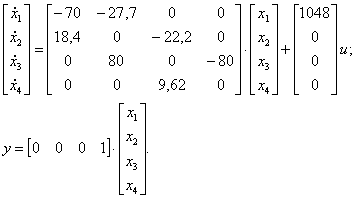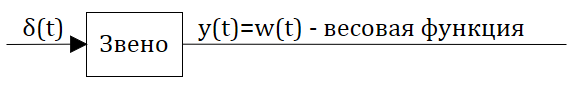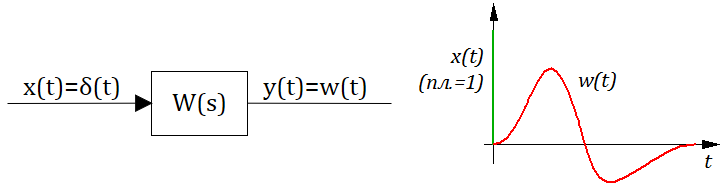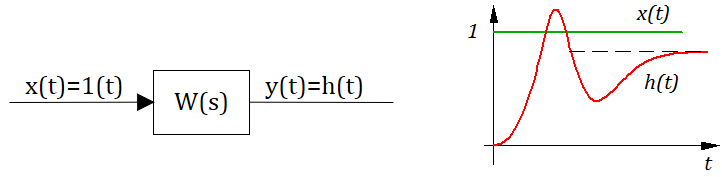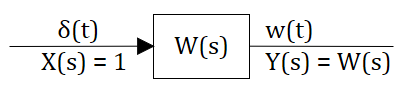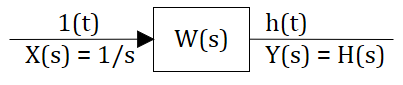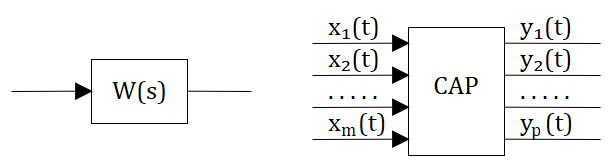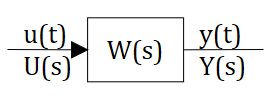- ТАУ Модели «вход – состояние – выход»
- Понятие пространства состояний
- y 2 ( t )
- u 1 ( t )
- u 2 ( t )
- u m ( t )
- x 1 ( t )
- x 2 ( t )
- x n ( t )
- y 1 ( t )
- y n ( t )
- W 1 ( s )
- W 2 ( s )
- Канонические формы уравнений состояния
- Первая управляемая каноническая форма
- Модели состояние выход уравнение выхода
- Контрольные вопросы к лекции № 1.
- ОТВЕТЫ
- 2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
- 2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
- Пример
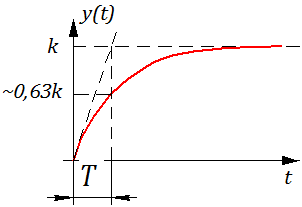
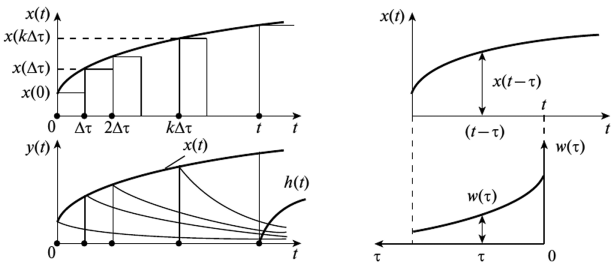
- 2.10. Весовая и переходная функции звена (системы).
- 2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
- 2.12. Mетод переменных состояния.
- Пример решения задачи в форме коши.
- 2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
- 2.13.1. Правая часть содержит только b0*u(t)
- 2.13.2. Правая часть общего вида
- Пример:
- 📹 Видео
Видео:2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

ТАУ Модели «вход – состояние – выход»
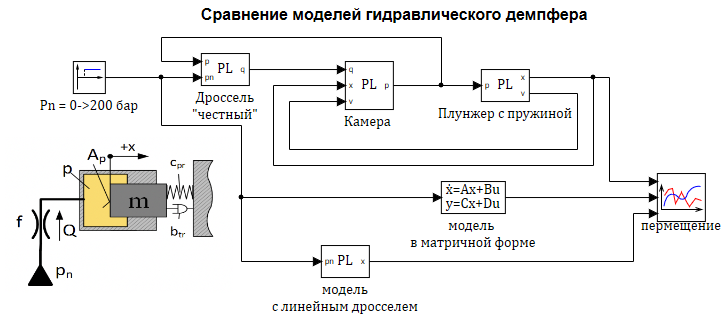
ТАУ предлагает два основных подхода к анализу и синтезу линейных САУ. Первый базируется на структурных схемах и ПФ отдельных элементов и всей системы. В связи с этим его часто называют операторно—структурным. Другой его особенностью является использование физических величин в качестве переменных. Подробно этот подход рассмотрен при изучении ММ типа «вход – выход» (см. п. 2.1).
Второй подход отличается описанием САУ системой ОДУ первого порядка, составленных относительно переменных состояния. Переменные состояния при таком описании САУ аналогичны обобщенным координатам, используемым в теоретической механике. Сам подход к исследованию САУ получил название метода пространства состояний или метода переменных состояния.
Понятие пространства состояний
Согласно методу пространства состояний (МПС) все переменные величины, характеризующие САУ, разделяют на три группы:
1) входные переменные или входные (управляющие) воздействия u m ;
2) выходные переменные y p , характеризующие реакцию САУ на входные воздействия;
3) переменные (координаты) состояния x n , характеризующие динамическое поведение САУ.
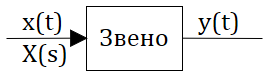
Взаимосвязь названных переменных поясняют схемой САУ, на которой систему изображают в виде «черного ящика» в соответствии с рисунком 2.29.
Отдельные части САУ характеризуют ПФ W 1 (s) и W 2 (s). Как следует из схемы, переменные состояния x n являются промежуточными величинами. Их относят к содержимому «черного ящика». Следовательно, они скрыты от прямого наблюдения. Кроме того, переменные состояния
не всегда являются физическими величинами. Иногда для удобства математического моделирования САУ целенаправленно отказываются от физического содержания переменных состояния. Поэтому в общем случае x n (t) являются абстрактными переменными. Однако они должны однозначно выражаться через физические величины y p (t).
В общем случае исследуемую САУ считают многомерной (рисунок 2.29). Для упрощения работы с многомерными величинами их представляют в векторно-матричном виде. Так, совокупность входных переменных представляют в виде вектора входа совокупность выходных переменных – в виде вектора выхода а совокупность переменных состояния – в виде вектора состояния
Согласно МПС множество всех значений, которые может принять вектор входа U в момент времени t, образует пространство входа исследуемой САУ. Аналогично, множество всех значений, которые может принять вектор выхода Y в момент времени t, образует пространство выхода, а множество всех значений, которые может принять вектор состояния X в момент времени t, образует пространство состояний САУ.
Как было отмечено, векторно-матричные уравнения (2.82) описывают многомерную САУ. Эта же совокупность уравнений служит ММ одномерной САУ, т.е. системы с одним входом и одним выходом. При использовании МПС такие САУ часто называют системами со скалярным входом и выходом, так как входная и выходная величины являются скалярными. Уравнения состояния и выхода одномерной системы имеют вид
Видео:Урок 455. Уравнение ШрёдингераСкачать

Канонические формы уравнений состояния
Разработано множество эквивалентных форм (представлений) уравнений состояния, различающихся между собой видом матриц A , B и C . Одни из форм используются чаще, так как обладают в некоторых случаях известными преимуществами перед другими. Такие формы записи уравнений состояния называются каноническими. Считают, что удобство канонических форм заключается в следующем. Во-первых, канонические представления матриц обеспечивают минимальное количество ненулевых элементов, что заметно упрощает вычисления. Во-вторых, канонические представления приводят к простым алгоритмам синтеза оптимальных регуляторов замкнутых САУ /3/.
Таким образом, в результате приведения уравнений к канонической форме более простую структуру принимают две из трех матриц: A и B (управляемые формы) или A и C (наблюдаемые формы). Управляемые канонические формы используют при синтезе регулятора, а наблюдаемые канонические формы – при синтезе наблюдателя /23/.
Первая управляемая каноническая форма
Первой управляемой канонической формой называют специальные матрицы
Очевидно, что коэффициенты характеристического полинома A(s) составляют последний столбец матрицы A. Матрицы такого вида называют матрицами Фробениуса. Элементы таких матриц определяют без вычислений. Характеристический многочлен A(s) совпадает со знаменателем ПФ системы управления. Корни данного многочлена определяют устойчивость и качество переходных процессов в САУ.
Матрица входа B рассматриваемого канонического представления также имеет специальный вид. Вследствие скалярного входного воздействия матрица B представляет собой вектор-столбец, элементы которого также не требуется вычислять.
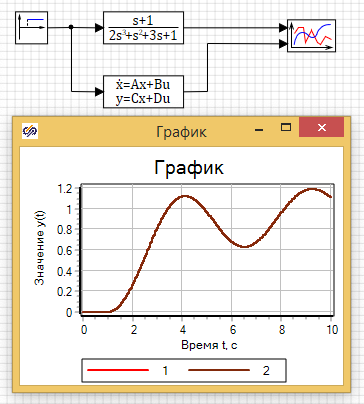
Полученная ММ системы управления может быть изображена в виде структурной схемы, представленной на рисунке 2.31.
Принятые переменные состояния являются выходными сигналами интеграторов.
Первую управляемую каноническую форму называют также канонической формой дуальной фазовой переменной /20/.
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Модели состояние выход уравнение выхода
Тема:«Векторно-матричные модели систем управления в непрерывном времени»
Понятие пространства состояний
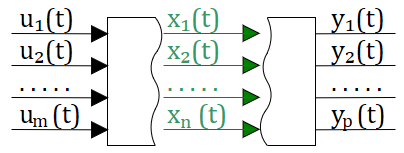
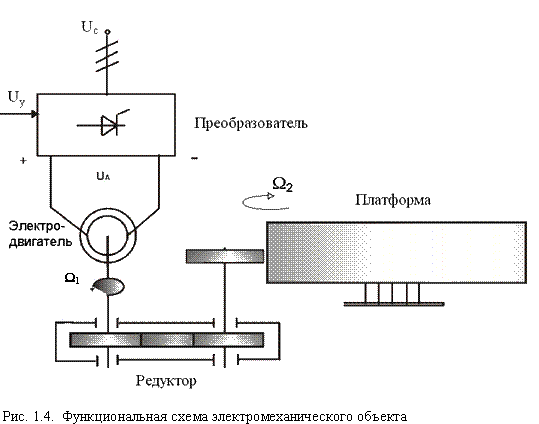
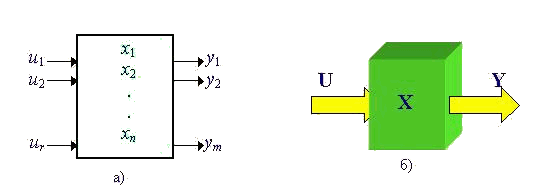
Современная теория автоматического управления оперирует с векторно-матричными моделями динамических систем. При этом рассматриваются в общем случае многомерные системы, т.е. системы произвольного порядка со многими входами и многими выходами, в связи, с чем широко используются векторно-матричные уравнения и аппарат векторной алгебры. Для получения векторно-матричной модели (ВММ) исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис. 1.1, а).
Рис.1.1. Скалярное (а) и векторное (б) представления динамической системы в виде «черного ящика»
Все переменные, характеризующие систему, можно разделить на три группы.
1. Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Они характеризуются вектором входа.
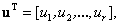
2. Выходные переменные, характеризующие реакцию системы на указанные входные воздействия. Представляются вектором выхода
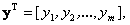
3. Промежуточные переменные, характеризующие внутреннее состояние системы, — переменные состояния, представляются вектором
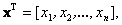
Таким образом, совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа u, совокупность выходов как вектор y, а совокупность промежуточных координат, характеризующих состояние системы, — в виде вектора состояния x (см. рис. 1.1, б).
Состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно.
Собственно система, ее входы и выходы — это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно математической моделью системы, заданием множеств входных и выходных переменных.
Решение задач анализа и синтеза связано с исследованием состояний системы, множество которых образует пространство состояний,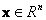
Векторно-матричные модели в непрерывном времени
В общем случае динамическая система в непрерывном может быть описана парой матричных уравнений:
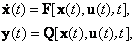 |
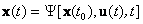 |
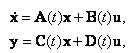 |
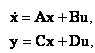 |
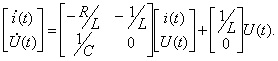 |
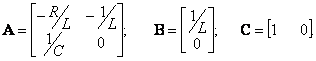 |
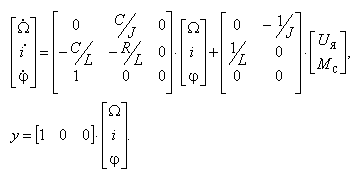 |
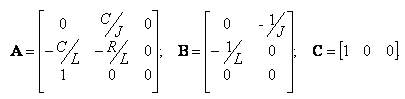 |
 |
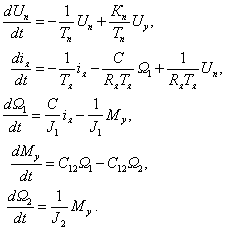 |
Если компонентами вектора состояния выбрать 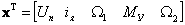
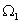
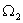
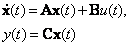 |
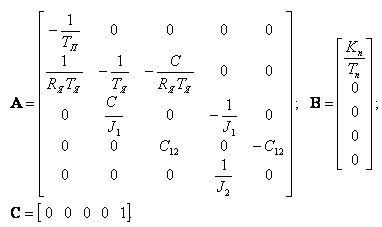 |
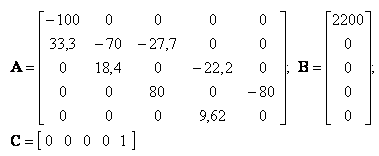 |









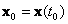 , дает вектор состояния системы
, дает вектор состояния системы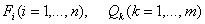 могут быть линейными комбинациями переменных состояния xi и входных переменных uq. При этом динамическая система описывается в векторно-матричной форме:
могут быть линейными комбинациями переменных состояния xi и входных переменных uq. При этом динамическая система описывается в векторно-матричной форме: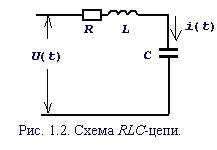
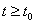 полностью определяется, если известны начальные значения
полностью определяется, если известны начальные значения 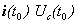 и входное напряжение U(t) при
и входное напряжение U(t) при 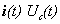 можно выбрать в качестве переменных состояния, то есть
можно выбрать в качестве переменных состояния, то есть 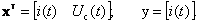
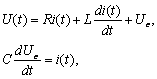
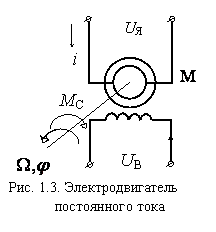
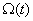 — скорости вращения ротора, тока якоря i(t), углового перемещения ротора
— скорости вращения ротора, тока якоря i(t), углового перемещения ротора 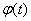 . При использовании знакомых зависимостей для электродвижущей силы
. При использовании знакомых зависимостей для электродвижущей силы 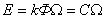 и вращающего момента двигателя
и вращающего момента двигателя 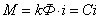 получим уравнение электрической цепи
получим уравнение электрической цепи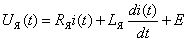
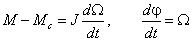
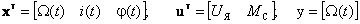 получим следующую векторно-матричную модель электродвигателя постоянного тока
получим следующую векторно-матричную модель электродвигателя постоянного тока
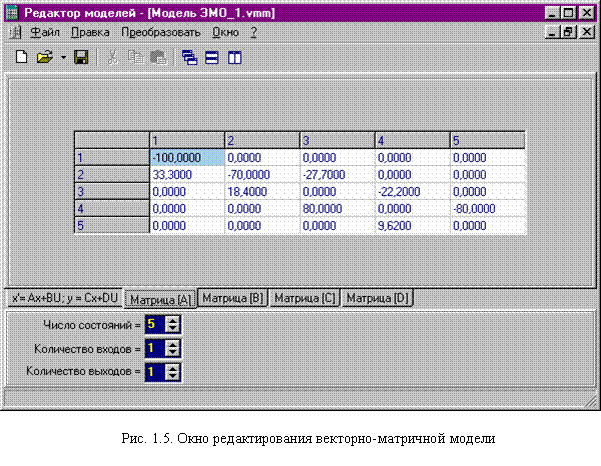
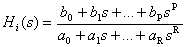
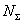 для описания этого объекта?
для описания этого объекта?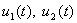 и одним выходом y(t) представлено следующим уравнением в операторной форме
и одним выходом y(t) представлено следующим уравнением в операторной форме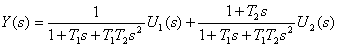
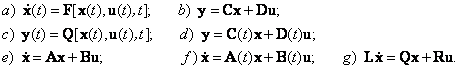
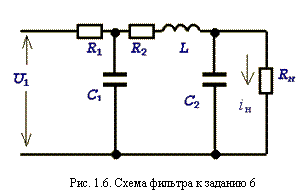
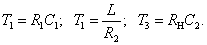
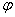 — угол поворота ротора электродвигателя,
— угол поворота ротора электродвигателя,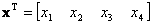 приведенной ниже векторно-матричной модели?
приведенной ниже векторно-матричной модели?