Модели движения роботов по заданным траекториям уравнение

Видео:ROS 4 Управление движением робота вдоль траекторииСкачать

Варианты передвижения робота на колесах

В общем случае робот может передвигаться прямолинейно и по ломанной траектории. Вычислить передвижение робота на необходимое расстояние по прямой достаточно просто. Для этого должен быть известен диаметр колеса робота. Исходя из этих начальных условий можно вычислить точное количество оборотов колеса, необходимое для преодоления заданного расстояния.

Видео:Мастер-класс "Движение по траектории роботов"Скачать

Робот за 3 минуты

Зная количество оборотов мотора робота в минуту можно вычислить время, за которое робот преодолеет нужное расстояние.

Для робота Lego EV3 количество оборотов большого мотора составляет 160 – 170 оборотов в минуту.

Поэтому вычисление времени будет приблизительным т.к. у каждого мотора количество оборотов в минуту может быть разным.

Ломанная траектория представляет из себя комбинацию из прямолинейных и криволинейных участков. Криволинейные участки можно вычислять, используя формулу вычисления длины окружности.

Видео:3D анимация в Mathcad: Движение робота-тележки по заданной траектории в виде фигуры ЛиссажуСкачать

Расчет числа оборотов

Для того, чтобы рассчитать количество оборотов колеса для движения на заданное расстояние по прямой нужно использовать длину окружности колеса. Она вычисляется по формуле L = π * d. Где π – число Пи, равное 3,14, а d –диаметр колеса. Для базового набора Lego EV3 диаметр колеса составляет 56 мм.

Пусть робот EV3 оснащен двумя передними колесами и шаровой опорой сзади и должен проехать 1 метр. За один оборот колеса робот преодолевает расстояние L = π * d = 3.14 * 56 = 175,84 мм. Пусть n – количество оборотов, k – заданное расстояние. Тогда количество оборотов n = k / L =>

n = 1000 мм / 175,84 мм = 5,69 оборотов.

Программа для Lego EV3 для движения робота на заданное количество оборотов.

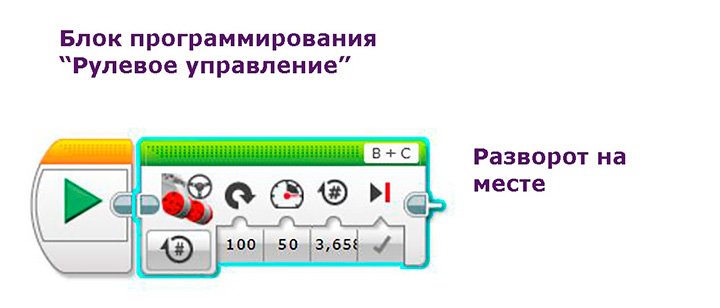
1. Во вкладке «Движение» выбираю блок «Рулевое управление».

Устанавливаю режим «Включить на количество оборотов», «Рулевое управление» установлено в 0 – это означает движение по прямой линии. Большие моторы установлены в порты B и C.

Скорость движения моторов – 50 условных единиц. Значение оборотов ставлю вычисленное выше. Тормозить в конце – значение «Истина». При нажатии на блок «Начало» робот Lego EV3 проедет по прямой 1 метр со скоростью 50 у.е. и остановиться.

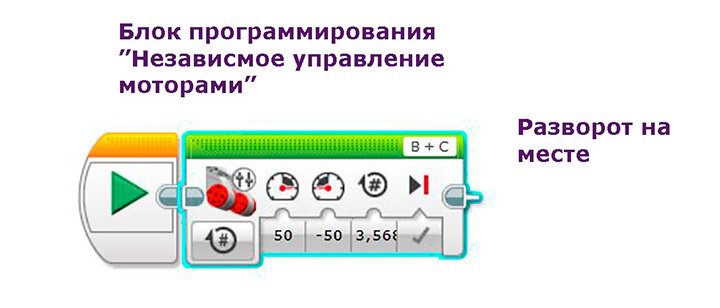
1. При втором способе используется блок «Независимое управление моторами».

независимое управление движение вперед на один метр

Все настройки блока такие же, как и настройки у блока «Рулевое управление». Для того чтобы робот ехал по прямой необходимо скорость моторов установить одинаковой.

В общем случае робот может передвигаться по траектории, которая представляет из себя окружность, часть окружности и комбинации различных частей окружности. При этом робот может:

1. Разворачиваться на месте – колеса робота крутятся в разные стороны с одинаковой скоростью;
2. Разворачиваться вокруг одного колеса – одно колесо машинки Lego EV3 стоит на месте, другое крутится с заданной скоростью;
3. Описывать произвольную окружность – оба колеса крутятся в одном направлении с разной скоростью.

Пусть параметры тележки EV3 будут такими: робот представляет из себя платформу с двумя колесами и шаровой опорой, расположенной сзади. Тележка симметрична и расстояние между центральными осями колес и шаровой опорой является равнобедренным треугольником.

робот тележка лего

Для упрощения расчетов, задам расстояние между центрами колес по оси, но которой они расположены равным 20 см. На многих соревнованиях по робототехнике одним из условий являются габариты робота. Например, нужно чтобы размеры робота были не более 20 см в ширину, 20 см в длину и 20 см в высоту.

Если робот не подходит по габаритам, то его не допускают к соревнованиям. Диаметр колеса 0,56 см – это стандартный размер колеса из базового набора Lego EV3. Левый большой мотор подключен к порту В, правый к порту С. Теперь вычислим количество оборотов колеса для каждого случая и для разворота робота Lego EV3 на определенный угол.

Расчеты применимы для роботов, собранных на базе любых конструкторов. Разница будет заключаться только в среде программирования, т.к. у разных робототехнических наборов разные программные обеспечения. Но принцип расчета везде одинаковый.

Видео:Математические модели и методы объекто-ориентированного моделирования робототехнических устройств.Скачать

Разворот на месте

1. Разворот робота на 360 градусов

В этом случае нужно чтобы у робота колеса вращались в разных направлениях с одинаковой скоростью. Для того чтобы робот совершил полный разворот вычислим необходимую длину окружности. Разворот будет на месте, поэтому диаметр между осями будет равен 20 см =>

Длина описываемой окружности будет равна
L = π * d = 3.14 * 0,2 м = 0,628 метра

Количество оборотов будет равно пройденному расстоянию L деленному на длину окружности колеса n = Lокр / L колеса, где длина окружности колеса равна L = π * d = 3.14 * 56 = 175,84 мм = 0,176 м.

А значит количество оборотов для разворота на 360° будет равно

n = L окр / L колеса = 0,628 / 0,176 = 3,568 оборота.

Для блока программирования «Рулевое управление» можно задать разворот на 100 условных единиц (или — 100), что означает разворот на месте. Скорость 50 у.е. и 3,568 оборота.

разворот робота на месте рулевое управление

Для блока программирования «Независимое управление моторами» просто скорость одного мотора ставим 50 у.е., а другого – 50 у.е. При этом количество оборотов колес остается 3,568.

разворот робота на месте независимое управление

1. Для того, чтобы повернуть робота тележку Lego EV3 на произвольное количество градусов нужно составить пропорцию, где нужное количество градусов нужно разделить на 360 градусов и учесть эту пропорцию в расчете.

Например, для разворота на 180 градусов. Обозначим нужную длину части окружности L1 =>

L1 = L * (нужное к-во градусов / 360 градусов) = L * (180 / 360) = L / 2 = 0,628 / 2 = 0,314, а значит к-во оборотов

n = L1 / L колеса = 0,314 / 0,176 = 1,784 оборота.

Видео:Уравнение движенияСкачать

Поворот вокруг одного колеса

В этом случае у нас радиус поворота будет 20 см, а диаметр описываемой окружности 40 см. Поэтому длина описываемой окружности будет в два раза больше и как для полной окружности, так и для ее части нужно просто предыдущие вычисления умножить на два.

Поворот робота вокруг одного колеса

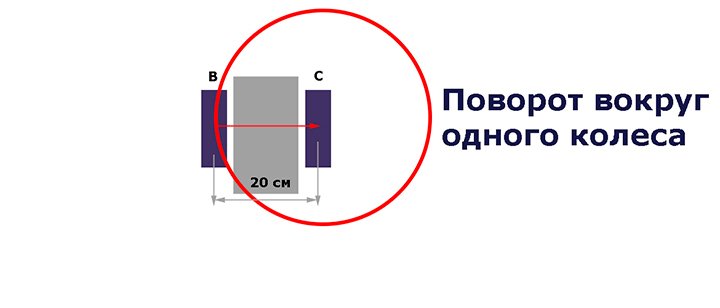
Для того чтобы сделать поворот вокруг одного колеса на 360 градусов нам понадобится в предыдущей формуле d умножить на 2, а значит и количество оборотов колеса увеличится вдвое.

L = π * 2 * d = 3.14 *2 * 0,2 м = 1,256 метра

Для робота собранного на базе набора Lego EV3 целесообразно применить программирование с помощью блока «Независимое управление моторами». Где одному мотору задать нулевое значение оборотов, а другому вычисленное. При повороте на 360 градусов это будет 7,136 оборота.

Видео:GMP – 4. Моделируем роботаСкачать

Движение по окружности произвольного диаметра

Пусть расстояние от центра окружности до середины первого колеса будет R1. Расстояние от центра окружности до середины второго колеса R2.

В этом случае мы получаем движение колес по окружностям разного диаметра за одинаковое время. Регулировать такое передвижение можно за счет разности скоростей внешнего и внутреннего колеса.

Длина окружности, которую проезжает правое колесо обозначим как L1

Движение робота по окружности произвольного размера

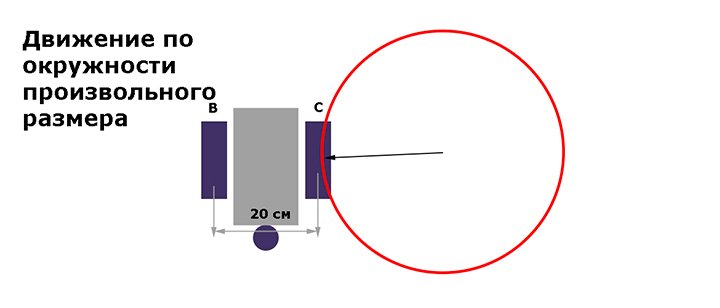
L1 = 2 * π * R1

Длина окружности для левого колеса

L1 = 2 * π * (R1 + R2)

Скорость правого колеса V1, а скорость правого колеса V2.
Время за которое заданное расстояние пройдет правое колесо t1.

t1 = L1 / V1 = (2 * π * R1) / V1

Время, за которое заданное расстояние пройдет левое колесо t2.

t2 = L2 / V2 = (2 * π * (R1 + R2)) / V2

Время проезда окружности или ее части левым и правым колесом у нас одинаковое t = t1 = t2, а значит и правые части выражений равны.

L1 / V1 = L2 / V2 ó (2 * π * R1) / V1 = (2 * π * (R1 + R2)) / V2 ó

Упрощаем выражение и получаем следующую пропорцию

V2 / V1 = (R1 + R2) / R1

Сейчас можно вычислить скорости левого и правого колеса для заданной окружности. Пусть у нас R1 = 20 см и R2 = 20 см, для упрощения скорость левого колеса возьмем 100 условных единиц. Тогда

V2 / V1 = (R1 + R2) / R1 ó 100 / V1 = (20 + 20) / 20

100 / V1 = 2 ó V1 = 100 / 2 ó V1 = 50 условных единиц.

Имея вычисленные значения скоростей можно составить программу прохождения участка. Для робота Lego EV3 можно использовать блок программирования «Независимое управление моторами». Скорость левого двигателя устанавливаем 100 у.е., скорость правого двигателя устанавливаем 50 у.е.

Независимое управление моторами Lego EV3 произвольная окружность

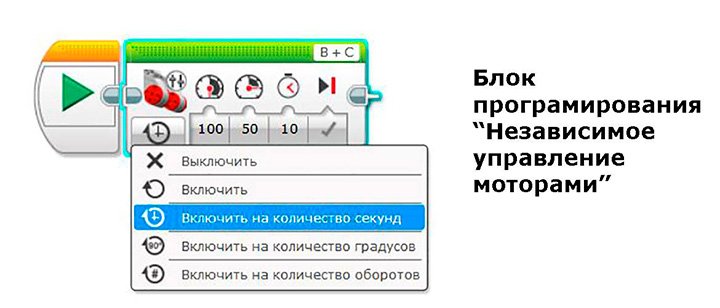
Режим устанавливаем «Включить на количество секунд». Произвольно установим 10 секунд. Для того, чтобы точно проходить заданное расстояние нужно замерить время прохождения одного круга секундомером. Зная это время можно задавать нужное нам расстояние.

Часто на соревнованиях одним из заданий является движение робота по черной линии с объездом препятствий. И для успешного преодоления трассы необходимо вычислить траекторию объезда. При помощи таких вычислений это сделать достаточно легко.

Видео:Как сделать робота с памятью команд (траектории движения)Скачать

Движение по линии с объездом препятствия (кирпич)

Видео:ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Модели движения роботов по заданным траекториям уравнение

В предыдущей статье « Начало работы с операционной системой для робота (ROS) » мы познакомились с основными понятиями и установкой операционной системы роботов ROS и с программой – имитатором робота Gazebo. Как ранее уже упоминалось, цель этой серии статей – помочь читателю создать автономный мобильный робот с нуля. Перемещаться этот робот будет с помощью колес. Проектируемый нами робот будет оснащен двумя ведущими колесами, которые мы установим на противоположных сторонах шасси. Управлять направлением движения мы будем с помощью разности скорости вращения ведущих колес. Например, если скорость вращения правого колеса будет меньше, чем скорость вращения левого, робот будет поворачивать вправо, и наоборот, если правое колесо будет вращаться быстрее левого, робот будет поворачивать влево.

Серия статей на тему: «Создание с нуля автономного мобильного обслуживающего робота с использованием Python»

Эта статья поможет вам провести математический анализ движения робота и решить уравнение кинематики робота. Уравнение кинематики даст вам возможность с помощью данных, получаемых от датчиков робота, предсказать его положение во время движения.

В этой статье будут рассмотрены следующие темы:

• математическое моделирование робота;
• введение в систему дифференциального привода и кинематику робота;
• инверсная кинематика.

Видео:5 СТРАШНЫХ вещей сказанных роботамиСкачать

Математическое моделирование робота

Наиболее важная часть мобильного робота – это система управления. С помощью нее робот ориентируется и перемещается в пространстве. Одной из самых простых и рентабельных систем управления является система дифференциального привода. Дифференциальный привод состоит из двух независимых друг от друга ведущих колес, установленных на общей оси. Каждое ведущее колесо приводится в движение отдельным двигателем. Дифференциальный привод – это неголономная система, которая имеет ограничения в изменении положения робота. Примером неголономной системы является автомобиль, поскольку он не может изменить положение без изменения
позы. Таким образом, имея три степени свободы (3D), автомобиль с помощью газа, тормоза и рулевого управления может использовать только две степени свободы (2D).

Напомним, голономная система – это механическая система, все механические связи которой можно свести к геометрическим. Такие связи накладывают ограничения только на положение системы, но не на величины скоростей.

Механической связью называют ограничения, накладываемые на координаты и скорости механической системы, которые должны выполняться на любом ее движении.

Если все кинематические связи нельзя свести к геометрическим связям, то данная система будет неголономной. Таким образом, неголономная система – это механическая система, на которую, кроме геометрических связей, наложены еще и дифференциальные (кинематические). Их нельзя свести к геометрическим связям.

Далее мы рассмотрим работу робота с дифференциальным приводом и возможность смоделировать его математически.

Видео:Лекция 3. Кинематика. Вероятностные модели движенияСкачать

Введение в систему дифференциального привода и кинематику робота

Кинематика – изучение движения объекта с точки зрения математики. Она рассматривает движение объекта без учета влияющих на него внешних сил. Здесь в основном внимание привлекает геометрическое отношение деталей, обеспечивающих управление конструкцией. Динамика – это исследование движения объекта с учетом всех сил, влияющих на робота.

Мобильный робот имеет шесть степеней свободы (DOF). Три степени свободы: х, у и z — связаны с тремя координатными осями, позволяющими определить положение объекта в трехмерном пространстве. Остальные три степени свободы относятся к ориентации робота в пространстве. Это такие значения, как крен (боковой наклон, или раскачивание корпуса робота относительно оси движения), тангаж (наклон аппарата относительно горизонтальной поперечной оси, т. е. наклон вниз или подъем вверх передка робота) и рыскание (небольшие изменения направления движения аппарата вправо или влево относительно его курса). Робот с дифференциальным приводом перемещается в двухмерной плоскости (2D), и его положение в любой момент можно описать двумя глобальными координатами Х и Y, лежащими в горизонтальной плоскости. При этом курс робота обозначается как θ. Этих данных вполне достаточно, чтобы описать положение робота с дифференциальным приводом.

Как уже говорилось ранее, дифференциальный привод робота основан на разности между скоростью вращения правого и левого ведущих колес. Если скорость вращения ведущих колес одинакова, робот движется прямо. При изменении скорости вращения одного ведущего колеса относительно другого робот будет выполнять поворот в ту сторону, в которой скорость вращения ведущего колеса меньше по отношению ко второму ведущему колесу. Ниже на фото представлена пара популярных роботов с дифференциальным приводом:

iRobot Roomba Pioneer 3-DX

Видео:Движение по траектории с препятствиямиСкачать

Прямая кинематика дифференциального робота

С помощью уравнений кинематики для робота с дифференциальным приводом определяется положение устройства. Представим, что начальное положение робота в момент времени t – X, Y, θ. Нам требуется определить, какое положение устройство займет (X′, Y′, θ′) за промежуток времени t + dt. При этом следует учесть следующие параметры: v-left – скорость левого и v-right – скорость правого колеса.

Эта методика расчета положения используется для проводки робота по требуемой траектории.

Объяснение уравнений прямой кинематики

Объяснение уравнения кинематики мы можем начать с формулирования решения для движения робота вперед без учета его массы и действующих на объект сил. Показанное ниже фото иллюстрирует кинематику одного из колес робота:

Колесо робота, вращающееся по локальной оси Y

Наклон вправо или влево относительно оси Y называется креном; все остальное можно рассматривать как скольжение. Предположим, что колесо не проскальзывает. В этом случае за один оборот обод колеса пройдет расстояние, равное 2πr, где r – радиус колеса. Будем считать, что движение происходит в двухмерной плоскости с плоской ровной поверхностью. Выполняя поворот, робот будет поворачиваться вокруг точки, находящейся на оси, совпадающей с осью правого и левого ведущих колес. Эта точка находится за пределами робота и называется мгновенным центром кривизны (ICC). На следующем фото вы увидите конфигурацию ведущих колес робота с дифференциальным приводом по отношению к точке мгновенного центра кривизны (ICC).

Конфигурация колеса робота с дифференциальным приводом

Основное понятие, без которого не получится вывести уравнение кинематического привода, – это угловая скорость робота, обозначаемая буквой w. При повороте ведущие колеса робота катятся по окружности, центр которой совпадает с мгновенным центром кривизны (ICC). Скорость колеса описывается формулой v = 2πr/T, где T – время, затраченное на прохождение колесом расстояния, равного длине полной окружности с центром, совпадающим с точкой ICC. Угловая скорость w определяется как 2π/T и измеряется в радианах (градусах) в секунду. Радиан – это угол, соответствующий дуге, длина которой равна радиусу этой дуги. 1 радиан равен 57,3°.

Если объединить уравнения для расчета скорости колеса v и его угловой скорости w, получим уравнение w = 2π/T.

(уравнение линейной скорости)

Схема дифференциального привода показана на следующем фото:

Детальная схема системы дифференциального привода

Если применить предыдущее уравнение к обоим ведущим колесам, результат будет одинаковым, т. е. w:

w(R + l/2) = Vr. (2)
w(R – l/2) = Vl. (3)

(уравнение дифференциального привода колес робота)

При этом R – расстояние между ICC и центром оси, проходящей через колеса, а l – длина оси колеса. Преобразовав выражения w и R, мы получим следующий результат:

R = l/2(Vl + Vr)/(Vr – Vl); (4)
w = (Vr – Vl)/l. (5)

(уравнение для вычисления расстояния от ICC до центра оси робота и расчета угловой скорости робота)

Предыдущие уравнения позволяют решать поставленные перед нами задачи кинематики. Предположим, что робот движется с угловой скоростью в течение wt секунд. В этом случае траектория движения и направление робота изменятся:

(уравнение для расчета изменения траектории движения)

Центр вращения ICC определяется базовой тригонометрией:

ICC = [ICCx, ICCy] = [x – Rsinq, y + Rcosq]. (7)

(уравнение для поиска ICC)

Поворот робота относительно ICC на угол ωδt в градусах

С учетом стартовой позиции (x, y) новое положение (х′, y′) может быть вычислено с помощью 2D-матрицы вращения. Учитывая движение робота с угловой скоростью ω в течение δt секунд относительно точки ICC, мы получим следующую позицию для времени t + δt:

(уравнение для вычисления новой позиции робота)

Учитывая ω, δt и R, новое положение робота (х′, y′ и θ′) можно вычислить с помощью уравнений (6) и (8). Угловая скорость ω вычисляется с помощью уравнения (5); точно измерить скорости Vr и Vl затруднительно.

Вместо непосредственного вычисления скорости колеса можно измерить его реальную скорость. Измерение реальной скорости производится с помощью энкодера. Энкодер – датчик, преобразующий подконтрольную величину в электрический сигнал. В нашем случае энкодер для определения угла поворота колеса вокруг своей оси фиксирует импульсы. Угол поворота колеса определяется количеством зафиксированных импульсов. В качестве рабочей величины применяется количество импульсов на один полный оборот колеса. Значениями одометрии робота являются данные от колесных энкодеров. Энкодеры установлены на осях колеса и передают двоичные сигналы для каждого шага вращения колеса (каждый шаг (step) равен 0,1 мм). Сигналы от энкодеров,
полученные за временной промежуток от t до t + δt, подаются на счетчик импульсов, в результате чего можно вычислить пройденное расстояние vδt:

Здесь n – количество импульсов, зафиксированных энкодером за заданное время.

Из этого можно вычислить v:

(уравнение для вычисления линейной скорости с помощью данных энкодера)

Если мы подставим уравнение (9) в уравнения (3) и (4), то получим следующий результат:

R = l/2(Vl + Vr)/(Vr – Vl) = l/2(nl + nr)/(nr – nl); (10)
wdt = (Vr – Vl)dt/l = (nr – nl)×step/l. (11)

(уравнение для вычисления R с помощью данных, полученных от энкодера)

Здесь nl и nr – количество импульсов, полученных от энкодеров левого и правого колес. Vl и Vr – это скорости левого и правого колес. Итак, робот перемещается с позиции (x, y, θ) в позицию (х′, y′, θ′). При этом от датчиков левого и правого колес в течение времени δt соответственно поступит nl и nr импульсов. В этом случае новое положение робота определяется по формуле:

(уравнение для вычисления положения робота с помощью данных, полученных от датчиков правого и левого колес)

R = l/2(nl + nr)/(nr – nl); (13)
wdt = (nr – nl)×step/l; (14)
ICC = [x – Rsinq, y + Rcosq]. (15)

(уравнение для вычисления ICC и других параметров с помощью данных,
полученных от датчиков правого и левого колес)

Полученное кинематическое уравнение в основном зависит от конструкции и размеров деталей ходовой части робота. Изменение конструкции может привести к корректировке уравнений.

Обратная кинематика

C помощью уравнений прямой кинематики мы можем определить новое положение робота, учитывая скорость вращения колеса. Теперь можно приступить к обратной задаче.

Допустим, робот в момент времени t находится в положении (х, y, θ). Определим скорости левого (V-left) и правого (V-right) колес так, что за промежуток времени t + δt робот займет новое положение с координатами (х′, y′ и θ′).

В устройствах с дифференциальным приводом переместить робота в нужную позицию с помощью только простой установки скорости вращения колес нельзя. Как уже упоминалось ранее, дифференциальный привод – это неголономная механическая система, в которой, кроме геометрических, учитываются и кинематические связи. Неголономная система накладывает некоторые ограничения на управление роботами.

Для увеличения степени подвижности (управляемости) неголономного робота следует использовать разность скоростей левого и правого колес. Если вставить значения из уравнений (12) в уравнение (15), то можно определить способы управления, которые в дальнейшем сможем запрограммировать:

• если V-left = V-right, => nr = nl => R = ∞, wdT = 0 (т. е. скорость и направление вращения левого ведущего колеса совпадают со скоростью и направлением вращения правого колеса), значит, робот движется прямолинейно и q остается неизменной;
• если V-left = –V-right, => nr = –nl, => R = 0, wdT = 2nl × step/l и ICC = [ICCx, ICCy] = [x, y] => x′ = x, y′ = y, θ′ = θ + ωδt => (т. е. скорости вращения левого и правого колес одинаковы, но направления их вращения не совпадают, колеса вращаются навстречу друг другу), значит, робот вращается вокруг мгновенного центра кривизны (ICC), т. е. ∀q может изменяться без ограничений при неизменных координатах [x, y].

Объединяя приведенные ниже способы управления, можно создать алгоритм, позволяющий достичь любого положения робота относительно его начального положения:

1) поворачивайте, пока ориентация робота не совпадет с линией, ведущей из исходного в целевое положение, V-right = –V-left = V-rot (скорость поворота);
2) двигайтесь прямо до тех пор, пока положение робота не совпадет с целевым положением, V-right = V-left = V-ahead (скорость прямого движения);
3) поворачивайте, пока ориентация робота не совпадет с ориентацией цели, V-right = –V-left = V-rot. Скорости V-rot и V-ahead выбираются произвольно.

Видео:Константин Яковлев | Методы и алгоритмы планирования траекторий движения в мобильной робототехникеСкачать

Итоги

Эта статья была посвящена не только фундаментальным концепциям роботов с дифференциальным приводом, но и кинематическим уравнениям движения таких устройств. В начале статьи были рассмотрены основы дифференциального привода роботов. Далее мы вывели использующиеся в таких устройствах уравнения прямой кинематики и объяснили их с помощью кинематических схем. Затем познакомились с уравнениями обратной кинематики. В следующей статье « Моделирование робота с дифференциальным приводом » рассмотрим, как с помощью ROS и Gazebo создать модель автономного мобильного робота.

Видео:Как создаются руки робота | PromobotСкачать

Реферат на тему «ПРОЕКТИРОВАНИЕ ТРАЕКТОРИЙ ПЕРЕМЕЩЕНИЯ РОБОТОВ»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

«ПРОЕКТИРОВАНИЕ ТРАЕКТОРИЙ ПЕРЕМЕЩЕНИЯ РОБОТОВ»

Мы изучили, каким образом можно описать задачу робототехнического манипулирования при помощи однородных преобразований; теперь нужно рассмотреть методы проектирования траекторий перемещения робота.

Рис. 4.7.1. Робот, размещающий МОП-пластины. (С разрешения PRI .)

Нужно описать желаемые движения манипуляционных роботов либо в пространстве обобщенных координат, либо в трехмерном рабочем пространстве, либо в координатах схвата в зависимости от того, интересуют ли нас зависимости от времени положения, ориентации, линейной скорости, угловой скорости, линейного ускорения и углового ускорения (рис. 4.7.1).

С точки зрения интересов человека-оператора робототехническая система должна быть способна позаботиться о деталях траектории движения, как только введены преобразования, описывающие задачу. Например, оператор может просто ввести желаемое кинематическое положение схвата робота для манипулирования объектом и предоставить системе управления роботом планировать форму траектории перемещения и такие детали, как профили изменения скорости и ускорения. Это определенным образом связано с так называемым программированием на уровне задачи, которое будет рассмотрено и гл. 9. Мы же обратимся к вопросу о том, каким образом траектории перемещения роботов интерпретируются управляющей ЭВМ и каким образом управляющая ЭВМ в действительности строит такие траектории и выдает команды роботу на выполнение желаемых задач. Цифровой природой управляющей ЭВМ обусловлено то, что генерация траекторий осуществляется дискретным образом. Так, генерация каждой дискретной точки на траектории движения происходит за так называемое время просчета траектории. Точки могут генерироваться с частотой 10—300 Гц в зависимости от того, какая частота вычисления точек траектории может быть достигнута на управляющей ЭВМ. Задача состоит в том, чтобы переместить схват робота из начального кинематического положения Н(0) в заданное кинематическое положение H ( t ) за время t . Естественным представляется описать движение гораздо более детально, чем определить лишь начальную и конечную точки, с тем чтобы избежать столкновений с предметами, находящимися в рабочей области. Таким образом, определяются промежуточные точки, в которых должно быть найдено кинематическое положение схвата робота. Для более подробно описанных траекторий должны быть определены значения обобщенной скорости и обобщенного ускорения. Очевидно, чтобы получить изменяющееся во времени кинематическое положение схвата робота Н( t ), необходимо прибегнуть к множеству изменяющихся во времени углов в сочленениях, или, иначе, к зависящему от времени вектору углов в сочленениях Q ( t ), такому, что

(4.7.1)

где ( t ) — не что иное, как зависящее от времени решение об- ратной задачи кинематики с начальным Н(0) и конечным Н( t ) кинематическими положениями схвата робота.

Далее мы опишем множество способов, применяемых для планирования и генерации желаемых векторов углов в сочленениях манипулятора.

КУБИЧЕСКИЕ ЗАКОНЫ ИЗМЕНЕНИЯ УГЛОВ В СОЧЛЕНЕНИЯХ

Простейший и наиболее часто используемый способ определения закона изменения угла в сочленении _i ( t ) — это определение начального и конечного значений _i ( t ) и _i ( t ), которые обычно принимают следующие значения:

_i (0) = _i0 (4.7.2)

_i (t_f) = _if (4.7.3)

_i (0) = 0 (4.7.4)

_i (t_f) = 0 (4.7.5)

где t_f — конечный момент времени, а к схвату робота предъявляется требование, чтобы он находился в состоянии покоя в начальный момент времени t =0 и достигал состояния покоя в момент времени t = t .

Условиям (4.7.2) — (4.7.5) могут удовлетворить многочлены третьей степени от времени, т. е.

_i (t)= _i0 + a_1it + a_2it 2 + a_3it 3 , (4.7.6)

_if = _i0 + a_1it_f + a_2it 2 _f + a_3it 3 _f, (4.7.7) 0 = a_1i, (4.7.8)

откуда a_2i и a_3i получаются равными

a_2i = 3( if — _i0 ) t -2 _f, (4.7.10)

a _{3 i} = 2( if — _{i 0} ) t -3 _f . (4.7.11)

Если начальная и конечная скорости не равны нулю, как в ситуации с роботом, отслеживающим движение конвейера, коэффициенты полинома получаются из условий выполнения следующих ограничений:

_i (0) = _{i 0} , (4.7.12)

_i ( t_f ) = _if . (4.7.13)

После этого легко определить коэффициенты в формуле (4.7.6):

a_ix = _i0 , (4.7.14)

a_2i = 3( if — _i0 ) t -2 _f — _i0 t_f -1 — _if t_f -1 (4.7.15)

a_3i = 2( if — _i0 ) t -3 _f + ( _i0 + _if), (4.7.16)

Заметим, что соотношения (4.7.14) — (4.7.16) носят достаточно общий характер, чтобы быть применимыми к любой промежуточной точке между начальной и конечной точками траектории. Однако вследствие требования непрерывности положения, скорости и ускорения решение уравнений относительно коэффициентов становится более сложным.

Найдите коэффициенты для двух кубических законов изменения углов в сочленениях, приняв равными продолжительности прохождения по обоим участкам траектории. Решение. Заметим, что в этом случае для первого и второго участков траектории движения

₁ (t)= a₁₀ + a₁₁t + a₁₂t 2 + a₁₃t 3 , (4.7.17)

₂ (t)= a₂₀ + a₂₁t + a₂₂t 2 + a₂₃t 3 . (4.7.18)

Ограничения имеют вид

₁ (0) = ₁₀ , ₂ (0)= ₁ ( t_{f 1} ); (4.7.19) ₁ ( t )= ₁₀ , ₂ (0)= ₁ ( t_{f 1} ); (4.7.20)

₂ ( t_{f 2} )= _{2 f} , ₂ ( t_{f 2} )= _{2 f} ; (4.7.21)

₁ (0) = ₁₀, ₂(0)= ₁( t_{f 1} ); (4.7.22)

Из приведенных восьми формул могут быть найдены восемь коэффициентов a ₁₀ , a ₁₁ , a ₁₂ , a ₁₃ , a ₂₀ , a ₂₁ , a ₂₂ , и a ₂₃ (см.домашнее задание 6)

Рис. 4.7.5. Сложное движение манипулятора.

ОБЩИЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ТРАЕКТОРИЙ

Вообще говоря, при планировании траектории робота нужно учитывать следующие обстоятельства.

1. Когда схват поднимает предмет, его движение должно быть направлено от опорной поверхности, чтобы избежать столкновения с ней.

2. Конечная точка подъема предмета должна лежать на нормали к поверхности, а начало системы координат схвата должно пройти через эту точку. Таким образом, будет обеспечено допустимое движение схвата. Контроль за скоростью, с которой должен подниматься предмет, может осуществляться путем слежения за временем, требуемым для перехода в эту точку.

3. Расстояние от конечной точки подъема до опорной поверхности рекомендуется выбирать равным не меньше 25 % длины последнего звена робота (0.25 d ₆ + длина инструмента) (рис. 4.8.1).

4. Требования 1 — 3 относятся и к начальной точке спуска, т. е. схват должен перемещаться в направлении, перпендикулярном поверхности, и замедляться при подходе к опорной поверхности.

5. Из приведенных выше соображений следует, что на каждой траектории робота имеются четыре типа точек — начальная точка, конечная точка подъема, начальная точка спуска, конечная точка (рис. 4.8.2).

Таким образом, на процесс планирования траектории можно наложить следующие ограничения.

1. Начальное положение фиксировано.

2. Начальная скорость обычно равна нулю.

3. Начальное ускорение обычно равно нулю.

4. Конечное положение фиксировано.

5. Конечная скорость обычно равна нулю.

6. Конечное ускорение обычно равно нулю.

7. Конечная точка подъема должна находиться от опорной поверхности на расстоянии 0.25 d ₆ + длина инструмента.

8. Начальная точка спуска должна находиться от опорной поверхности на расстоянии 0.25 d ₆ + длина инструмента.

Рис. 4.8.1. Рекомендуемая конечная точка подъема.

Рис. 4.8.2. Типичная траектория движения i -го сочленения.

К перечисленным выше ограничениям можно также добавить, ограничения на скорость и ускорение в промежуточных положениях, т. е. в точках подъема и спуска. Однако, опустив эти ограничения, мы будем иметь восемь ограничений, которые можно было бы удовлетворить полиномом с неизвестными коэффициентами не менее чем седьмой степени. Так, для любого угла в сочленении _i можно записать

_i ( t ) = a_ni t n , (4.8.1)

где a_ni — элементы матрицы размера 8 x i .

Так как это выражение — полином седьмой степени, возможно, он будет иметь значительное число экстремумов (максимумов и минимумов), что было бы нежелательно для траекторий перемещения роботов. Кроме того, вычисление всех неизвестных коэффициентов может занять много времени (если i = 6,имеем 48 коэффициентов).

Ограничения, относящиеся к траекториям сочленений

📸 Видео

Семинар 31. Планирование траектории колесного робота с использованием численных NMPC-решателейСкачать

ИМРС 3.2 Прямая и обратная задачи кинематики для плоского робота с двумя вращательными сочленениямиСкачать

Система управления колесным агротехническим роботом.Скачать

Что нужно знать робототехникуСкачать

Методика оценки погрешности позиционирования промышленного роботаСкачать