В 1963 г. американский экономист У. Шарп предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа.
В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две переменные величины — независимую Х и зависимую Y линейным выражением типа Y = α + β Х. В модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи rm, вычисленную на основе индекса Standart and Poor’s (S&P500). В качестве зависимой переменной берется отдача ri какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&P500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно
модель Шарпа называют рыночной моделью,
а норму отдачи rm — рыночной
Пусть норма отдачи rm принимает случайные значения и в течение N шагов расчета наблюдались величины rm1, rm²,…, rmN. При этом доходность ri какой-то i-ой ценной бумаги имела значения ri1, ri2,…, riN. В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами rm и ri в любой наблюдаемый момент времени в виде:
ri,t = αi + βirm,t + εi,t (4)
где: ri,t — доходность i-ой ценной бумаги в момент времени t;
αi — параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг rm;
βi — параметр линейной регрессии, называемый «бета»,
показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;
rm,t — доходность рыночного портфеля в момент t;
εi,t — случайная ошибка, свидетельствующая о том, что реальные, действующие значения ri,t и rm,t порою отклоняются от линейной зависимости.
Особое значение необходимо уделить параметру βi, поскольку он определяет чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности.
Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:

где Wi — вес каждой ценной бумаги в портфеле
Дисперсия портфеля в модели Шарпа представляется в виде:

Цели инвестора сводятся к следующему:
необходимо найти минимальное значение дисперсии портфеля при следующих начальных условиях



шарп дисперсия портфель ковариация
Итак, отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:
) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности ri,t каждой ценной бумаги.
) По рыночному индексу вычислить рыночные доходности rm,t для того же промежутка времени.
) Определить величину дисперсии рыночного показателя σm, а также значения ковариаций σi,m доходностей каждой ценной бумаги с рыночной нормой отдачи и найти величины βi:

4) Найти ожидаемые доходности каждой ценной бумаги E(ri) и рыночной доходности E(rm) и вычислить параметр αi:
αi = E(ri) — βiE(rm) (11)
5) Вычислить дисперсии σ2ε,i ошибок регрессионной модели
) Подставить эти значения в соответствующие уравнения
После такой подстановки выяснится, что неизвестными величинами являются веса Wi ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля E*, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель. [1]
Видео:Линейная регрессияСкачать

Модель оценки капитальных активов (модель Шарпа)
Ожидаемую доходность актива можно определить с помощью так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов.
Простая индексная модель предложена У. Шарпом в середине 60-х гг. Ее часто называют рыночной моделью. В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Она предполагается линейной. Уравнение модели имеет следующий вид:
где E(ri ) – ожидаемая доходность актива; γi – доходность актива в отсутствие воздействия на него рыночных факторов; βi – коэффициент в актива; Ε(rm) – ожидаемая доходность рыночного портфеля; Εi , – независимая случайная (переменная) ошибка.
Независимая случайная ошибка показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней величины равно нулю. Она имеет постоянную дисперсию ковариации с доходностью рынка, равную нулю; ковариацию с нерыночным компонентом доходности других активов, равную нулю.
Приведенное уравнение является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных (Ε) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь. Тогда модель Шарпа принимает следующий вид:
где Ε(rp) – ожидаемая доходность портфеля; βρ – β портфеля; γρ – доходность портфеля в отсутствие воздействия на него рыночных факторов.
Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Модель Шарпа. САРМ.
Читайте также:
|
| σmi |
| μ |
| SML |
| μm |
| M |
| r |
 |
бета – это мера того, насколько поведение акции похоже на поведение рынка в целом.
Бета измеряет вклад актива в портфельный риск. Бета средней акции равна единице.
β > 1 – агрессивные акции. Сильно зависят от рыночной конъюнктуры.
β = 1 – средние акции. Средне зависят от рыночной конъюнктуры
2. САРМ предполагает, что рынок находится в равновесии. Однако это, во-первых, гипотеза, во-вторых, можно задать различные типы равновесия, причем все они будут эмпирически неопределимы.
3. Модель САРМ основывается на гипотезе о поведении инвестора и, в частности, о форме кривой безразличия. Поскольку в модели появляются полезности, то она непроверяема по той причине, что еще никто эти полезности не измерил.
Дата добавления: 2015-04-18 ; просмотров: 18 ; Нарушение авторских прав
📽️ Видео
Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Линейная регрессияСкачать

Математика #1 | Корреляция и регрессияСкачать

Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

#3. Линейная модель. Понятие переобучения | Машинное обучениеСкачать

Множественная Линейная Регрессия || Машинное ОбучениеСкачать

Эконометрика. Линейная парная регрессияСкачать

Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать
![Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]](https://i.ytimg.com/vi/y--76SrfRm8/0.jpg)
РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать
Лекция 2.1: Линейная регрессия.Скачать

Лекция. Регуляризация в линейной регрессииСкачать

Множественная регрессияСкачать

Логистическая Регрессия | Logistic Regression | Линейная модель для классификации |МАШИННОЕ ОБУЧЕНИЕСкачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Лекция 8. Линейная регрессияСкачать

Парная регрессия: линейная зависимостьСкачать

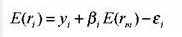
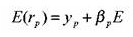
 либо
либо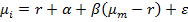 , где
, где )
)

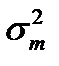 – вариации рыночного портфеля;
– вариации рыночного портфеля; – ковариации доходности i-го актива с доходностью рынка в целом.
– ковариации доходности i-го актива с доходностью рынка в целом.