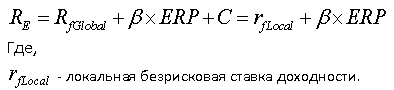Модель сарм предпосылки модели основное уравнение модели

Распространенным подходом к оценке уровня премий за акционерный риск, применяемым на практике основными инвестбанками и аудиторами, является модель САРМ (Capital Asset Pricing Model), другое название – модель ценообразования на рынке капитальных финансовых активов, изредка в учебной литературе встречается аббревиатура МОДА, то есть «модель оценки долгосрочных активов».

Модель CAPM, чаще всего, применяется для объяснения динамики курсов ценных бумаг и функционирования механизма, посредством которого инвесторы могли бы оценивать влияние инвестиций в предполагаемые ценные бумаги на риск и доходность их портфеля.

Концепция этой модели была разработана в 1950-х гг. в США Гарри Марковицем [1], дальнейшее развитие модель получила в работах Jack Treynor (1961-1962гг.), William Sharpe (1964г.), John Lintner (1965г.) и Jan Mossin (1966г.).

Суть САРМ модели заключается в следующем: предполагая существование высоколиквидного эффективного рынка финансовых активов, можно прийти к выводу о том, что величина требуемой отдачи на средства, вложенные в какой-либо актив, определяется не столько специфическим риском, присущим конкретному активу, сколько общим уровнем риска, характерным для фондового рынка.[2]

Такой вывод может показаться противоречащим здравому смыслу – инвестору должен быть компенсирован тот риск, который он принимает, вкладывая ресурсы в капитал компании. Логика модели базируется на том, что инвестор диверсифицирует свои вложения и, хотя для разных вложений, входящих в портфель активов инвестора, характерен разный профиль риска, зачастую потери от одного актива могут быть компенсированы доходами по другому активу, что существенным образом снижает реальный уровень риска, принимаемого на себя инвестором.

Математически формула определения ожидаемой ставки доходности на долгосрочный актив имеет следующий вид:

где,
Rf — доходность безрисковых активов, под которой, как правило, понимают доходность государственных ценных бумаг;
Rm — ожидаемая средняя норма прибыли рыночного портфеля;
(Rm-Rf) — премия за риск вложения в акции (в ряде учебных пособий премия за рыночный риск принимается равной 5%);
β — коэффициент, характеризующий чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности).

Смысл модели CAPM заключается в том, что требуемая (рыночная) доходность собственного капитала есть безрисковая ставка доходности, увеличенная на риски, соответствующие акционерному капиталу.

Применительно к российской практике можно говорить о двух подходах для расчета по модели CAPM для компаний из развивающихся рынков.

Подходы к расчету модели CAPM:

Страновой риск корректируется на β-коэффициент

Страновой риск не корректируется на β-коэффициент

Если страновой риск корректируется на β-коэффициент, формула для CAPM принимает следующий вид:

В случае, когда страновой риск не корректируется на β-коэффициент, формула для CAPM принимает следующий вид:

Для непубличных компаний вышеприведенные формулы CAPM для расчета ставки дисконтирования могут дополняться показателями S1 и S2 — премиями за малый размер и специфические риски соответственно.

где,
S1 — дополнительная норма дохода за риск инвестирования в конкретную компанию;
S2 — дополнительная норма дохода за риск инвестирования в малую компанию.

Говоря о безрисковой ставке, следует пояснить, что различают несколько безрисковых ставок: глобальную безрисковую ставку и локальную безрисковую ставку.

Глобальная безрисковая ставка – ставка по государственным облигациям США, Англии, Германии и Швейцарии. (Информацию по американским государственным облигациям можно найти тут). В качестве глобальной безрисковой ставки доходности правильнее выбирать ставку доходности по 10-летним американским государственным облигациям.

Локальная безрисковая ставка – ставка по российским государственным облигациям номинированным в рублях (данные о ставке можно посмотреть здесь).

Среднерыночная доходность (Rm) представляет собой доходность рыночного портфеля. В качестве данного показателя берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (Индекс ММВБ, Nikkei 225 и т.п.), данные значения легко можно найти в открытом доступе.

Безрисковая доходность (Rf) представляет собой, ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на изменение краткосрочной ликвидности и инфляцию. Единого мнения в отношении значения показателя нет. Так, американские финансовые аналитики полагают, что в качестве доходности безрисковых активов следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать долго- или краткосрочные, – единства нет.

Разницу между среднерыночной нормой доходности акций и безрисковой ставкой (Rм — Rf) называют премией за риск вложения в акции (equity risk premium, ERP).

Размер премии за риск инвестирования в акционерный капитал, ERP. В качестве ERP можно взять готовую цифру из верифицированного источника аналитических данных. К примеру для России, на 01.01.2015 ERP составлял 13,72%, а для западных компаний обычно эта премия варьируется в диапазоне 3,5% — 6%.

Бета-коэффициент характеризует чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности – доходности того или иного фондового индекса).

β-коэффициент выражает меру систематического риска для акций компании. Величина коэффициента определяется на основе анализа ретроспективных данных соответствующими статистическими службами фирм, специализирующихся на рынке информационно-аналитических услуг, инвестиционными и консалтинговыми компаниями и публикуется в финансовых справочниках и периодических изданиях, анализирующих фондовые рынки. Общий алгоритм расчета показателя в следующей таблице:

Общий алгоритм расчета показателя

Отметим, информацию о бета-коэффициенте публичных компаний можно взять в виде готовой цифры из открытых источников, к примеру, для акций ГМК «Норильский никель» на 25.12.15 значение коэффициента равно 0,88.

Если необходимо рассчитать значение бета-коэффициента для непубличной компании, то можно воспользоваться формулой Хамады [6]:

Рассмотрим пример расчета бета-коэффициента для непубличной компании, занимающейся производством пищевых продуктов (скачать).

Известны достаточно простые алгоритмы, позволяющие найти приблизительное значение бета-коэффициента для данной ценной бумаги. Пусть Kij — доходность акций i-й компании в j-м году, a Kmj — доходность на рынке в среднем (j = 1, 2, . n) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании (ΔKij) к приращению среднерыночной доходности (ΔKmj):

Алгоритм, задаваемый формулой, весьма приблизителен, поскольку приращения можно считать различными способами. Достаточно часто используется следующий вариант расчета β:

1. определяются средние (например, по годам) значения доходности акций данной компании и по рынку в целом;
2. строится уравнение линейной регрессии, отражающее зависимость средней доходности акций данной компании от доходности на рынке в среднем;
3. коэффициент регрессии (т.е. коэффициент при параметре Km) и будет бета-коэффициентом.

Так как данные для расчета CAPM базируются на процентных ставках номинированных в долларах США, то при использовании рублевых денежных потоков необходимо скорректировать полученную величину ставки дисконтирования по следующей формуле:

где,
Rrur — ставка дисконтирования, номинированная в рублях;
Rusd — ставка дисконтирования, номинированная в долларах США;
Brur — доходность по рублевым государственным облигациям России;
Busd — доходность по еврооблигациям России, номинированным в долларах США.[4]

Одним из основных преимуществ в применении модели является то что, модель CAРM позволяет учесть влияние внешних факторов, не зависящих от хода реализации проекта, – страновые и политические риски, ставки доходности (без рисковые, отраслевые и среднерыночные). При этом, правда, следует учитывать и ее недостатки, к которым можно отнести:

1. Имеет прямое отношение только к компаниям, которые являются открытыми акционерными обществами и, следовательно, их акциями торгуют на фондовых рынках.
2. Вызывает затруднения при определении, какие из вложений можно считать без рисковыми, применим только к компаниям, которые располагают достаточной статистикой для расчета своего коэффициента бета или имеют возможность найти компанию-аналог, чей коэффициент бета мог бы использоваться в расчетах.

При использовании в модели информации зарубежных фондовых рынков в ставке дисконта необходимо учитывать дополнительный риск, связанный с инвестированием средств в Россию (страновой риск). Уровень риска инвестирования в конкретную страну определяется крупнейшими информационно-аналитическими и рейтинговыми агентствами.

Capital Asset Pricing Model, САРМ – центральная концепция современной финансовой экономики. Эта модель дает представление о том, какое должно быть соотношение между риском вложения в актив и доходностью этого вложения. Эта формула нашла широкое применение в теории современного инвестиционного анализа в самых различных его областях: оценки прибыльности проектов, портфельных инвестиций, оценки предприятий.

Видео:Тема 4 Модели ценообразования финансовых активов модель Марковица и CAPMСкачать

Модель CAPM – что это простыми словами, пример расчета

CAPM (Capital Asset Pricing Model) – одна из методик оценки стоимости активов акционерного общества с точки зрения рисков, присущих как непосредственно оцениваемому активу, так и рынку в целом.

Модель CAPM построена на предположении: инвесторы заинтересованы в получении дохода выше, чем доход по безрисковым активам.

CAPM – это метод, который может применяться в теории, на практике его использование возможно лишь в некоторых случаях, в комбинации с другими методиками.

Сегодня мы рассмотрим модель оценки капитальных активов CAPM: формулу расчета этого показателя, его применение на практике, преимущества и недостатки.

Видео:4 3 Использование модели САРМ для определения требСкачать

Что такое модель CAPM

Как известно, стоимость акционерного общества определяется стоимостью его активов. В данном случае под активами понимают не основные фонды, а финансовые инструменты, эмитентом которых является предприятие.

Предпосылкой CAPM стала гипотеза эффективного рынка капитала, появившаяся в начале XX века. Эта гипотеза основана на том, что рынок является прозрачным, и любые изменения быстро отражаются на стоимости акций. В целом рынок «заточен» на долгосрочные инвестиции.

Современная модель оценки капитальных активов была разработана в середине XX века американским экономистом Гарри Марковицем. Далее метод CAPM был взят на вооружение другими финансовыми гуру: Джоном Линтнером, Джеком Л. Трейнором и Уильямом Шарпом. Последний в 1964 г. разработал модификацию модели, которая используется по сей день. Иногда модель капитальных активов CAPM называют моделью Шарпа.

Итак, на чем основана CAPM model? Попытаемся объяснить простыми словами.

Предположим, есть некий безрисковый актив с минимальной доходностью и практически нулевой волатильностью. Безрисковым средством в модели CAPM обычно выступают государственные облигации. Помимо этого, в портфеле мы имеем акции предприятия нефтедобывающего комплекса. Эти бумаги могут принести неплохой доход, однако уж очень зависят от внешней ситуации, в том числе политической. Какова цель инвестора? Как сбалансировать портфель?

Если наш инвестор очень осторожен, то в его портфеле будут преобладать ОФЗ. Да, он не получит высокий доход, но и ничего не потеряет. А если он все-таки хочет, чтобы его деньги работали и приносили прибыль, то он будет двигаться в сторону увеличения доли бумаг с высокой волатильностью. При этом должно соблюдаться общее правило: если эти бумаги начнут падать и приносить убыток, общая должность портфеля не должна быть ниже, чем ставка доходности по ОФЗ.

Для чего необходима модель оценки капитальных активов

Итак, на чем основана модель оценки капитальных активов? Инвестор должен представлять, какой доход он может получить за то, что рискует своими деньгами.

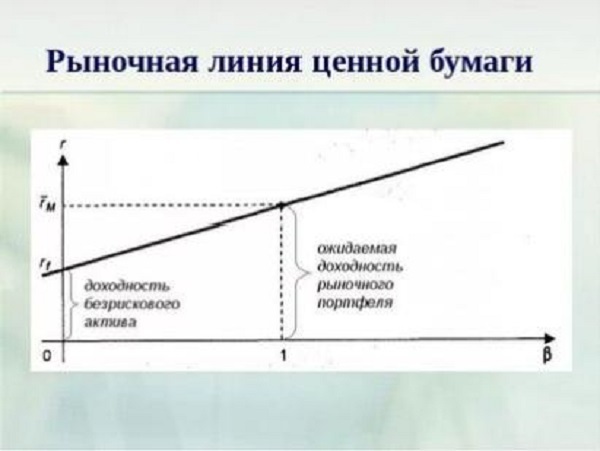
Наглядно CAPM представлена на графике:

Модель CAPM описывает зависимость между доходностью актива, ставкой по безрисковым инструментам и рыночному риску в целом.

CAPM включает элементы:

• доходность безрискового актива;
• ожидаемая общая доходность портфеля;
• общая рыночная доходность;
• чувствительность инструмента к колебаниям рынка (коэффициент β).

Итак, CAPM применяется для оценки доходности ценной бумаги или проекта с учетом систематического (недиверсифицируемого) риска.

Недиверсифицируемый риск – это риск, связанный с отсутствием стабильности в получении дохода. Так, в одном году доходность может быть максимальная, а в следующем периоде оказаться нулевой. Подобные риски присущи ценным бумагам российских компаний, в т.ч. «голубым фишкам».

Возникает резонный вопрос: как рассчитывать или где взять значение коэффициента β? Этот показатель берется из данных статистики. Можно рассчитать коэффициент самостоятельно, используя функции линейной регрессии в Excel, что мы и сделаем в примере ниже. Для этого нужны данные доходности за определенный период по анализируемому активу и в целом по рынку. Для российских бумаг обычно используются индексы РТС или ММВБ, для зарубежных – S&P 500, NASDAQ и др.

Поскольку значения индекса основаны на данных за предыдущие периоды, а само понятие систематического риска говорит о непредсказуемости изменения цены и доходности инструмента, применять расчеты на практике следует с осторожностью. Тем не менее рассчитаем Capital Asset Pricing Model по формуле и в Excel, используя данные по котировкам, находящиеся в свободном доступе.

Видео:5 1 Предпосылки и свойства модели APT видео фрагмент 1Скачать

Формула расчета

Формула CAPM выглядит так:

[ RE=Rf + β*(Rm – Rf), где: ]

​ ( RE ) ​ – ожидаемая ставка;

​ ( Rf ) ​– ставка по безрисковым инструментам;

​ ( Rm ) ​ – усредненная прибыль по портфелю в целом;

​ ( β ) ​ – коэффициент чувствительности актива к колебаниям рынка.

Например, средняя ставка по ОФЗ – 4%. Ожидаемая доходность по портфелю – 20%. Коэффициент β – 0,5.

Приведем таблицу значений β:

Значение	Комментарий
β > 1	Инструмент чувствителен к колебаниям рынка
β = 1	Доходность актива равна доходности по рынку
0 Читайте также Фишинг — что это значит, какую цель преследует и как он работает [ RE=4 + 0.5 х (20 – 4)=12%. ] Таким образом, инвестор ожидает, что инструмент будет приносить доход в размере 12%. Видео:WACC - Средневзвешенная стоимость капитала (+CAPM)Скачать Расчет модели CAPM в Excel Приведем пример расчета модели CAMP с использованием редактора Excel. Исходные данные будут такие: анализируемый инструмент – акции Tesla; рыночная доходность определяется по индексу NASDAQ; безрисковый актив – 30-летние облигации США, средняя ставка доходности по ним в 2020 году – 1,51%. Месяц NASDAQ TSLA r_NASDAQ r_TSLA Rf β Rm RE (formula CAMP) Янв. ’20 9 150,94 130,11 1,51% 3,17 3,46% 7,69% Февр. ’20 8 567,37 133,60 -6% 3% Март ’20 7 700,10 104,80 -10% -22% Апр. ’20 8 889,55 156,38 15% 49% Май ’20 9 489,87 167,00 7% 7% Июнь ’20 10 058,76 215,96 6% 29% Июль ’20 10 745,27 286,15 7% 33% Авг. ’20 11 775,46 498,32 10% 74% Сент. ’20 11 167,51 429,01 -5% -14% Окт. ’20 10 911,59 388,04 -2% -10% Нояб. ’20 12 198,74 567,60 12% 46% Дек. ’20 12 888,28 705,67 6% 24% Коэффициент β посчитан способом линейной регрессии между доходностями по акциям Tesla и индексу NASDAQ и составляет 3,17. Как мы помним, значение больше единицы указывает на то, что акции чувствительны к изменению рыночной доходности. [ RE=Rf + β х (Rm – Rf)=1,51% + 3,17 х (3,46% – 1,51%)=7,69%. ] Ожидаемая доходность выше ставки по безрисковым бумагам и значительно выше рыночной доходности Rm, которая рассчитана как среднее значение по индексу NASDAQ. Видео:4 3 Модель оценки капитальных активов CAPM видео фрагмент 4Скачать Как устроена модель CAPM Модель ценообразования на капитальные активы предполагает следующее: Инвестор, который желает увеличить доходность, будет сокращать долю безрискового инструмента в своем портфеле до минимума. Структура рынка постоянно является оптимальной: на каждую единицу риска всегда приходится единица рыночной премии (разница между Rm и Rf). Коэффициент β отражает зависимость цены на акцию от колебаний рынка. Если доходность инструмента ниже значения RE, рассчитанного по модели оценки CAPM, то приобретать данный инструмент смысла не имеет. Видео:Оценка ставки дисконтирования по модели Шарпа (модель CAPM)Скачать Как можно использовать модель CAPM Базовая модель оценки капитальных активов соответствует критерию определения цены капитала: сумма ожидаемой прибыли деленная на количество ценных бумаг. Ожидаемая доходность рассчитывается с учетом рисков и чувствительности цены к изменениям общей ситуации на рынке. Модель CAPM исходит из того, что инвесторы могут варьировать структуру портфеля с учетом премии за риск. В свою очередь, финансовые менеджеры используют модель для расчета стоимости капитала компании. Видео:Использование САРМ для оценки проектовСкачать Где применяется модель CAPM Итак, основные задачи CAPM – определение цены капитала и премии за риск. В связи с этим модель можно использовать при расчете ставки дисконтирования. Области применения могут быть самые разные. Так, аналитики рассчитывают стоимость капитала по компании, ее подразделениям, фирмам-конкурентам и отрасли в целом. Инвестор, сравнивая ожидаемую прибыль с доходностью по безрисковым инструментам, принимает решение об увеличении или сокращении доли того или иного актива в портфеле. Видео:3 8 Модель ценообразования финансовых активов CAPMСкачать Преимущества и недостатки модели CAPM Перечислим плюсы использования модели: Базовая модель оценки капитальных активов соответствует основному принципу рынка: чем выше риск, тем больше потенциальная прибыль. Коэффициент бета является одним из важных показателей, характеризующих систематический риск. Несмотря на то, что эта величина рассчитывается несколько сложно (при помощи математических функций), ее отсутствие в других методиках дает менее точные результаты. Модель CAPM можно использовать для расчета ставки дисконтирования. Недостатки модели оценки капитальных активов заключаются в следующем: Метод не учитывает несколько важных факторов: отраслевые особенности, налогообложение, размеры компании и др. Модель ценообразования капитальных активов строится на основании данных за прошлые периоды, что не исключает вероятность ошибочных прогнозов. В самом деле, мы проанализировали акции Tesla и получили неплохой результат. А как долго можно на него ориентироваться, учитывая включение компании в другие индексы, например S&P 500? На этот вопрос вряд ли можно получить ответ. Расчет дает неверные результаты при отрицательной доходности. Видео:5.1 Основное уравнение теории ценообразования | курс Finmath for FintechСкачать Пример расчета Итак, модель оценки капитальных активов включает следующие компоненты: безрисковая ставка дохода (Rf); коэффициент β (уровень систематического риска); рыночная доходность (Rm). Рассмотрим простой пример расчета ставки дохода на собственный капитал (RE) по модели CAPM с использованием исходных данных: ​ ( Rf ) ​=5% (ставка по ОФЗ); Сначала рассчитаем премию за риск: [ RE=0,05 + 1,5 х 0,07=0,155 ] Таким образом, ставка дохода на собственный капитал составляет 15,5%. Видео:19 Модель ценообразования финансовых активов CAPMСкачать Заключение Базовая модель ценообразования на капитальные активы используется для оценки степени влияния риска на будущую доходность ценных бумаг. Применение CAPM в условиях кризисов может давать недостоверные результаты ввиду высокой волатильности рынка: возникает необходимость постоянно пересчитывать премию за риск, которая меняется практически каждый день. Ориентированная на долгосрочную перспективу, модель CAPM не подходит для такой ситуации. Как и любой другой инструмент расчета, модель оценки активов CAPM следует использовать в совокупности с другими методиками: WACC (средневзвешенная стоимость капитала), DDM (модель дисконтирования дивидендов) и др. Видео:Формула CAPM: расчетыСкачать Модель CAPM Для оценки риска при приобретении акций в основном используется модель CAPM. Концепция применяется на практике крупными инвесторами. Она была разработана в середине 50-х гг. американским экономистом Гарри Марковиц. В 60-е гг. изучению и развитию модели CAPM посвятили научные работы Джек Трейнор, лауреат Нобелевской премии Уильям Шарп и другие специалисты США. Модель CAPM – определение и суть CAPM – это распространенная модель для анализа и оценки ценности капитала при расчете доходности инвестиционного проекта по отношению к возможным рискам: чем они выше, тем больше должен быть уровень дохода. Суть CAMP заключается в предположении существования рынка финансовых активов с высокой ликвидностью. При его функционировании необходимый показатель отдачи на вложенные средства определяется не только специфическим, но и общим риском, который характерен для фондового рынка в целом. Концепция CAPM используется для понятия изменения курсов акций, других ценных бумаг и формирования механизма, необходимого для оценки рисков и показателя доходности. Видео:Модель CAPM. Безрисковая ставкаСкачать Формула расчета модели CAPM Для анализа ставки доходности, которую планируется получить в долгосрочной перспективе, используется математическая формула Шарпа: RЕ – ожидаемая ставка или показатель доходности; Rf – уровень дохода от ценных бумаг государства или активов, которые не обладают рисками; Rm – среднерыночная доходность или предполагаемая прибыль сформированного инвестиционного портфеля при среднем показателе; Rm – Rf – разница, которая показывает премию за риск инвестиций в процентах. В большинстве случаев значение равно около 5%; β – коэффициент для определения чувствительности отдельной акции к колебаниям доходности рыночной среды. Он вычисляется с учетом статистических сведений. Формула САРМ предполагает увеличение ожидаемого дохода от капитала с учетом степени риска. На территории Российской Федерации используются два подхода к применению модели: с корректировкой риска конкретной страны, который демонстрирует показатель прямого или косвенного риска на исполнения обязательств должником при влиянии действий правительства, по отношению к коэффициенту β; без корректировки. При использовании первого метода формула будет иметь следующий вид: RЕ = RfGlobal + β * ЕRР + С = RfLocal + β * ЕRР Видео:Тема 5 Модели ценообразования финансовых активов Теория арбитражного ценообразования Arbitrage PricСкачать Расчет модели CAPM в Excel (пример) Для упрощения проведения расчетов и минимизации возникновения ошибок математического характера специалисты используют Excel. За рыночный доход берется индекс RTSI (РТС) или ММВБ. В таблице Excel проставляются данные за конкретный период по индексу RTSI и по акциям организации. Для вычисления доходности акций необходимо из разницы между ячейками РТС за предыдущий и последний период разделить за значение предыдущего периода. В зависимости от расположения данных в ячейках электронной таблицы Excel формула будет иметь вид: Для получения индекса используется аналогичная формула, только для вычисления берется не РТС, а значение по акциям предприятия: E5=(С4-С3)/С3. Для определения доходности можно применять натуральный логарифм. В этом случае формула будет выглядеть так: =LN(B4/B3) и =LN(С4/С3). Итоги вне зависимости от используемого метода расчета будут одинаковыми. В столбце D будут содержатся информация по доходности рынка, а в Е – сведения по акциям конкретной компании. Расчет бета-коэффициента с помощью формул Excel для CAPM На втором этапе осуществляется вычисление коэффициента β, который отражает риск акции на рынке. Для этого требуется воспользоваться функциями ИНДЕКС и ЛИНЕЙН. Первая необходима для выборки значений из таблицы. Формула: D5:D250 – значения доходности акций (245 данных); Е5:Е250 – значения по ценным бумагам предприятия. При необходимости можно использовать второй метод. Расчет β через функцию «Регрессия» для CAPM Для вычисления риска рынка модели необходимо в главном меню найти раздел «Данные», затем категорию «Анализ данных». В диалоговом окошке следует выбрать «Регрессия». На завершающем этапе необходимо ввести интервалы: Е5:Е250 и D5:D250. В результате пользовательских действий на новом листе электронная таблица рассчитает параметры модели линейной регрессии – коэффициент β, и другие полезные значения. Расшифровка значения β в модели CAPM Коэффициент демонстрирует чувствительность динамики доходности ценных бумаг и рынка, то есть отражает рискованность инвестирования собственного капитала. Расшифровка коэффициента: β > 1 – ценная бумага реагирует на изменение дохода на рынке; β = 1 – доходность акции и рынка равны; 0 В Excel в формулу вводятся номера ячеек с соответствующими цифрами, полученными в результате вычислений: RЕ=F4+G4(H4-F4), где в столбце F производилось вычисление безрисковой ставки, в G – коэффициента β, а в H – среднего значения доходности рынка. Excel самостоятельно рассчитает ожидаемую ставку доходности. Видео:Агентная модель рынка. Урок 1Скачать Преимущества и недостатки модели CAMP САРМ необходима для определения цены акций и стоимости собственного капитала в будущем. Основное достоинство концепции – принцип тесной связи между рыночными рисками и величины будущей прибыли от ценных бумаг. Выделяется три недостатка CAPM: берется только один фактор, который влияет на будущий доход от акций. Но на практике на показатель также влияет сфера деятельности компании и ее масштабность; не учитываются налоговые ставки, трансакционные издержки и т.д.; используется ретроспективное состояние риска на рынке, что может привести к возникновению ошибок в прогнозировании. Недостатки способствовали возникновению ограничений на применение CAMP. Видео:8.9 Модель AD ASСкачать Ограничения в применении модели оценки САРМ капитальных активов Некоторые положения модели САРМ частично или полностью не могут быть выполнены в условиях реального рынка. Существует несколько ограничений в применении модели, она идеально работает при выполнении следующих условий: Отсутствие трансакционных затрат. Наличие эффективного рынка, при котором наблюдаются однородные ожидания инвесторов. Отсутствие налогообложения. Возможность вложения в безрисковые активы и привлечения дополнительного финансирования под безрисковую ставку по процентам. Коэффициент бета отражает полную меру риска. Модель оценки капитальных активов CAMP не является идеальной и имеет свои недостатки и ограничения. Но позволяет определить требуемый уровень дохода актива, который предполагается добавить к существующему рыночному портфелю инвестора с учетом риска 💡 Видео Построение расчётных моделей в Lira Sapr Урок 22 Корректировка расчётной модели в САПФИРСкачать Модель AD-AS, совокупный спрос, совокупное предложение, шоки, равновесиеСкачать 8.8 Причины колебаний экономической активности Модель AD ASСкачать Финансовая модель компании за 90 минутСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства