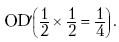Модель олигополии о курно уравнения кривых реагирования равновесие курно нэша равновесная цена (5 видео)

УСТАНОВЛЕНИЕ РАВНОВЕСИЯ В МОДЕЛИ КУРНО

Сделаем предположение, что на рынке существует только одно предприятие. Это предприятие выбирает, каким должен быть уровень выпуска, максимизирующий его прибыль. Затем на рынок входит другая фирма.

Допустим, что выбор объема выпуска фирмой 1 известен и что фирма 2 будет адаптироваться к этой ситуации и определит свой собственный объем производства, максимизирующий ее прибыль. Фирма 1 реагирует в свою очередь на выбор фирмы 2. Этот процесс приспособления (корректировки) проходит много этапов действий и реакций до тех пор, пока обе фирмы не достигнут равновесия и не будут больше заинтересованы в изменении объема выпуска продукции. Следовательно, каждая фирма уточняет свои предложения относительно поведения другой путем наблюдения за ее реальным выбором объема производства. Эта динамическая интерпретация показывает, что именно процесс обучения позволяет фирмам достичь точки равновесия. Однако в соответствии с наклоном кривых реакции можно прийти к разным результатам. Если кривая реакции фирмы 1 имеет более сильный (крутой) наклон, чем у фирмы 2, они достигнут равновесия Курно — Нэша, т.е. стабильного равновесия (рис. П.8.1-1). В противоположном случае равновесие будет нестабильным (рис. П.8.1-2).

Динамическая интерпретация является спорной в том смысле, что ничто априори не позволяет утверждать, что процесс обучения (приобретения опыта) приведет к схождению в точке равновесия. Равновесие существует (точка пересечения функций реакции), но если фирма 1 решает производить объем производства, отличный от равновесного количества товара, приспособляясь к условиям в зависимости от реакции фирмы 2, можно обнаружить несоответствие предположений. Теория nip позволяет решить эту проблему.

Современный анализ стратегического взаимодействия фирм в теории игр позволил прояснить определенные понятия (концепции). Каждая фирма должна угадать выбор другой фирмы, как в игре-считалке. Теория игр анализирует взаимодействие между рациональными игроками, принимающими решения индивидуально.

При проведении исследования следует учитывать три фактора: игроков, стратегии и доходы. Две фирмы представляют собой двух игроков, доходы представлены прибылями каждой фирмы; соот-

Рис. П.8.1-1. Стабильное равновесие:

— кривая реакции фирмы 1; R₂ — кривая реакции фирмы 2; q* — равновесный объем выпуска фирмы 1; q₂ — равновесный объем выпуска фирмы 2; С — точка пересечения кривых реакции R₁ и R₂, точка равновесия

Рис. П.8.1-2. Нестабильное равновесие:

— кривая реакции фирмы 1; R₂ — кривая реакции фирмы 2; q* — равновесный объем выпуска фирмы 1; q₂ — равновесный объем выпуска фирмы 2; С — точка пересечения кривых реакции и R₂, точка равновесия

ветственно, и стратегии представлены выбранными объемами производства, которые каждая фирма может производить.

Равновесию Курно — Нэша соответствует парное значение объемов выпуска (q‘, q₂), такое, которое каждое предприятие выбирает, чтобы максимизировать свою прибыль, принимая во внимание предположения относительно выбора другого предприятия, являющегося, по существу, действительно верным.

Пример решения на основе построения матрицы:

Выпуск ( 1 . Это сводит на нет дискуссии относительно сходимости к равновесию Курно.

Представим анализ дуополии Курно более формально. Пусть функция отраслевого спроса описывается линейной зависимостью

где Q — суммарное производство двух фирм;

q_x — объем выпуска, выбранный фирмой 1;

q₂ — объем выпуска, выбранный фирмой 2.

Каждая фирма имеет идентичные предельные издержки.

Обе фирмы выбирают такой объем производства, который максимизирует их прибыль с учетом реакции друг друга:

Решение уравнений для фирмы 1 выглядит следующим образом:

Далее найдем предельный доход фирмы: [1]

Как видно из уравнения предельного дохода фирмы 1, возможно два варианта решения:

1) фирма 1 предполагает, что выпуск фирмы 2 не изменится в ответ на ее собственный выбор q_v т.е. принимает q₂ как данный, фиксированный;
2) фирма 1 предполагает, что конкурент будет менять свой объем выпуска q₂, т.е. присутствуют предположительные вариации в ответ на предложение объема выпуска q_x фирмы 1.

В первом случае получим

Тогда, используя условия максимизации прибыли Л/Л, = Л/С,, получаем функцию реакции фирмы 1:

Данное уравнение описывает лучший выбор объема производства фирмы 1 — q для данного выбора q_v

Аналогично, решая уравнение Л//^ = МС₂ относительно объема выпуска фирмы 2, получим функцию реакции фирмы 2:

Таким образом, учитывая, что фирмы идентичны, можно записать:

В точке равновесия совпадают ожидания двух фирм. Обе фирмы в этом случае находятся на соответствующих кривых реакции в точке оптимума, т.е. точке их пересечения, и у них нет стимула менять объем производства, так как достигнута максимизация прибылей П, и П₂.

Для определения равновесного общего объема выпуска отрасли сложим (q + q) — Q и получим

Подставив в функцию спроса равновесный общий выпуск Q получим равновесную рыночную цену:

Рассмотрим второй случай, когда присутствуют предположительные вариации, т.е. допускается, что фирма 2 реагирует на установление объема выпуска фирмой 1 путем изменения своего уровня производства. В этом случае получаем

Решение равенства MR_<= МС_Х позволяет вывести функцию реакции при условии наличия предположительных вариаций:

В общем виде это равенство выглядит следующим образом:

где — предположительные вариации для фирмы /, при этом цена будет равна

Представим, что в модели Курно действуют не две фирмы, а несколько идентичных компаний. В общем случае их число равно N. Тогда совокупный спрос будет следующим:

Рыночная цена при этом равна

Используя выражение ()_, для обозначения суммы выпуска отрасли, за исключением фирмы 1, описать кривую спроса фирмы 1 можно следующим образом:

Прибыль фирмы 1 зависит и от над величиной которого она не имеет контроля, и от собственного уровня производства q_v который она может свободно выбирать. Учитывая, что предельные издержки фирмы 1 равны МС, ее прибыль может быть записана как

Максимизация прибыли требует: MR = Л/С,, тогда

Решение этого уравнения относительно q, дает нам функцию реакции фирмы 1, или ее лучшую ответную функцию:

Для того чтобы представить этот результат для любой фирмы, используем Q_. как совокупное производство отрасли, за исключением такового фирмы /. Это значит, что функция спроса для фирмы считая выпуск всех других фирм как данный, фиксированный, представлена в виде Р= (A — BQ_₍.) — Bq_r Тогда, рассуждая аналогично ситуации для фирмы 1, получаем лучшую функцию реакции для фирмы /:

В равновесии по Нэшу каждая фирма / выбирает лучший ответ

д], который отражает правильное предположение относительно объемов выпуска других (N — I) фирм. Обозначим Q, сумму всех объемов выпуска, за исключением [2] :

Между тем фирмы могут быть и неидентичными, т.е. иметь различные предельные издержки. Обратимся сначала к случаю двух фирм с различными издержками Л/С, и МС_Т Пусть функция спроса для фирмы 1 имеет вид Р—А — Bq₂ — Bq_v а функция предельного дохода Л//?, = A — Bq₂ — 2Bq_]

Решение уравнения максимизации прибыли Л/Л, = Л/С, для фирмы 1 дает ее лучшую функцию ответа, или реакции:

Аналогичные рассуждения приводят к получению лучшей функции ответа для фирмы 2:

В данном случае на функцию реакции каждой фирмы оказывают влияние их собственные различные предельные издержки в отличие от исходной модели дуополии Курно с идентичными фирмами. Например, если предельные издержки фирмы 2 увеличатся с МС₂ до МС₂‘, ее кривая реакции сдвинется внутрь, ближе к началу координат. Таким образом, объем выпуска фирмы 2 сократится, а объем производства фирмы 1 вырастет. Между тем новое равновесное состояние будет характеризоваться меньшим совокупным выпуском отрасли.

Видео:Теория Игр. Модель Курно. 29Скачать

Модель Курно. Равновесие Курно

Статический анализ взаимоотношения двух фирм в условиях дуополии был предложен в 1838 г. французским экономистом Антуаном Опостьеном Курно (1801-1877). Курно исходил из следующих предпосылок.

Обе фирмы (А и Б) производят однородный товар. Им известна кривая рыночного спроса. Обе фирмы принимают решения о производстве одновременно, самостоятельно и независимо друг от друга. Каждая из фирм предполагает выпуск конкурента постоянным, продавцы не могут иметь точной информации о своих ошибках (действуют «с завязанными глазами»). При этом возможны различные варианты Тарануха, Ю.В. Микроэкономика: учебник по специальности «Менеджмент организации» / Ю.В. Тарануха, Д.Н. Земляков. М., 2010. С.176.

Допустим, одна из фирм (например, Б) принимает решение о приостановке производства. Тогда рыночный спрос полностью обеспечивается выпуском фирмы А. Ее кривая спроса полностью совпадает с кривой рыночного спроса D₁(O) (рис. 3).

Рисунок 3 — Оптимизация объема производства фирмы А в зависимости от объема производства фирмы Б

При выборе максимизирующего прибыль объема производства фирма А решит производить 120 единиц товара, так как именно при этих условиях сравняются предельный доход MR₁(O) и предельные издержки МС. Если теперь фирма Б будет производить 40 единиц, то фирма А отреагирует на это сдвигом кривой спроса до положения D (40), а ее производство сократится до 40 (именно в этом случае MR₁ (40) = МС₁). Соответственно, когда фирма Б производит 60 единиц, фирма А уменьшает свой выпуск до 20 единиц, а когда фирма Б расширит производство до 120 единиц, фирма А вообще остановит свое производство.

Отмечая на графике (рис. 4), как меняется выпуск фирмы А в зависимости от изменения выпуска фирмой Б, мы получаем кривую реакции фирмы А — Q_A(Q_Б).

Аналогичный анализ можно осуществить и в отношении фирмы Б, получив в результате еще одну кривую реакции — Q_Б(Q_A). Пересечение кривых реагирования этих двух фирм (точка Е) показывает равновесие Курно: каждая фирма правильно угадывает поведение конкурента и принимает оптимальное для себя решение, ни одна из фирм не имеет стимула изменять свой объем производства.

Рисунок 4 — Равновесие Курно

Модель равновесия Курно предполагает, что фирмы-дуополисты конкурируют друг с другом. Ситуация принципиально изменится, если дуополисты договорятся друг с другом и будут коллективно намечать объем производства.

Рассмотрим этот случай, предполагая идентичность обеих фирм и линейную кривую спроса (рис. 5) Нуреев, Р.М. Курс микроэкономики: учебник / Р.М. Нуреев. М., 2008. С.210.

Рисунок 5 — Равновесие Курно, договорное равновесие и конкурентное равновесие

Равновесие Курно достигается, когда

а суммарный выпуск составляет 80 единиц. Если фирмы договорятся максимизировать совокупную прибыль, чтобы затем разделить ее пополам, то множество возможных решений этой задачи будет ложиться на контрактную кривую. При этом суммарный выпуск

Видео:Экономика. Олимпиады. Теория игр. Модели олигополии. Приоткрытый вебинар.Скачать

Модель дуополии Курно

Впервые попытку создать теорию олигополии предпринял французский математик, философ и экономист Антуан Огюстен Курно еще в 1838 г. Однако его книга, в которой излагалась эта теория, осталась незамеченной современниками. В 1863 г. он выпустил новую работу «Принципы теории богатства», где изложил старые положения своей теории, но без математических доказательств. Лишь в 70-е гг. XIX в. последователи стали развивать его идеи.

Модель Курно исходит из того, что на рынке действуют только две фирмы и каждая фирма принимает цену и объем производства конкурента неизменными, а затем принимает свое решение. Каждый из двух продавцов допускает, что его конкурент всегда будет удерживать свой выпуск стабильным. В модели предполагается, что продавцы не узнают о своих ошибках. Фактически же эти предположения продавцов о реакции конкурента, очевидно, изменятся, когда они узнают о своих предыдущих ошибках.

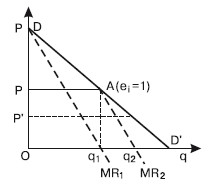
Модель Курно представлена на рис. 34.1.

Рис. 34.1. Модель дуополии Курно

Предположим, что первым начинает производство дуополист 1, который в первое время оказывается монополистом. Его выпуск (рис. 34.1) составляет Q_1; что при цене Р позволяет ему извлекать максимальную прибыль, ибо в этом случае MR = МС = 0. При данном объеме выпуска эластичность рыночного спроса равна единице, а общая выручка достигнет максимума.

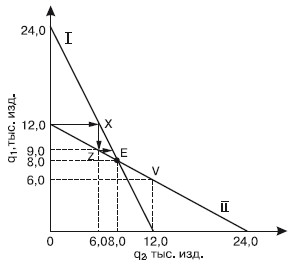
Затем производство начинает дуополист 2. В его представлении объем выпуска сдвинется вправо на величину OQ₁ и совместится с линией AQ₁. Сегмент AD’ кривой рыночного спроса DD он воспринимает как кривую остаточного спроса, которой соответствует кривая его предельной выручки MR₂. Выпуск дуополиста 2 будет равен половине неудовлетворенного дуополистом 1 спроса, т. е. сегмента Q₁D’, а величина его выпуска равна Q₁Q₂, что даст возможность получить максимум прибыли. Данный выпуск составит четверть всего рыночного объема спроса при нулевой цене,

На втором шаге дуополист 1, допуская, что выпуск дуополиста 2 сохранится стабильным, решит покрыть половину оставшегося все еще неудовлетворенным спроса. Исходя из того что дуополист 2 покрывает четверть рыночного спроса, выпуск дуополиста 1 на втором шаге составит

всего рыночного спроса, и т. д. С каждым последующим шагом выпуск дуополиста 1 будет уменьшаться, в то время как выпуск дуополиста 2 будет увеличиваться. Такой процесс окончится уравновешиванием их выпуска, и тогда дуополия достигнет состояния равновесия Курно.

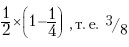
Модель Курно многие экономисты считали наивной по следующим основаниям. Модель допускает, что дуополисты не делают никаких выводов из ошибочности своих предположений относительно реакции конкурентов. Модель закрыта, т. е. число фирм ограничено и не меняется в процессе движения к равновесию. Модель ничего не говорит о возможной продолжительности этого движения. И наконец, нереальным представляется предположение о нулевых операционных издержках.

Равновесие в модели Курно можно изобразить через кривые реагирования, показывающие максимизирующие прибыль объемы выпуска, который будет осуществляться одной фирмой, если даны объемы выпуска конкурента.

На рис. 34.2 кривая реагирования I представляет максимизирующий прибыль выпуск первой фирмы как функцию от выпуска второй. Кривая реагирования II представляет максимизирующий прибыль выпуск второй фирмы как функцию от выпуска первой.

Рис. 34.2. Кривые реагирования

Кривые реагирования можно использовать для того, чтобы показать, как устанавливается равновесие. Если следовать стрелкам, нарисованным от одной кривой к другой, начиная с выпуска Q₁ = 12 ООО, то это приведет к осуществлению равновесия Курно в точке Е, в которой каждая фирма производит 8000 изделий. В точке Е пересекаются две кривые реагирования. Это и есть равновесие Курно.

КУРНО Антуан Огюстен (1801–1877), французский экономист, математик и философ, предшественник математической школы буржуазной политической экономии. В работе «Исследования математических принципов теории богатства» (1838) он предпринял попытку исследовать экономические явления с помощью математических методов. Им впервые была предложена формула D = F(P), где D – спрос; Р – цена, согласно которой спрос является функцией цены.