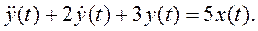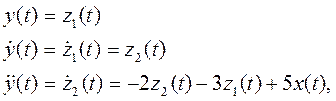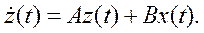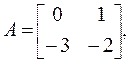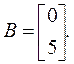Представление в переменных состояния основано на использовании теоремы Коши об эквивалентности представления обыкновенного дифференциального уравнения (ДУ) n-го порядка в виде системы n уравнений 1-го порядка.
Рассмотрим в качестве примера переход от описания модели в виде линейного дифференциального стационарного уравнения 2-го порядка к описанию модели в виде системы двух уравнений 1-го порядка, а затем – к стандартной модели в виде переменных состояния.
Пример. Пусть некая динамическая система описывается линейным ДУ 2-го порядка с постоянными коэффициентами:
и тогда можно выразить исходное уравнение в виде двух уравнений через состояния z1(t) и z2(t).
Запишем полученную систему из 2-х уравнений 1-го порядка в так называемом векторно-матричном виде:
где z(t) – вектор состояния; x(t) – вектор управления (в данном примере, в частности, x(t) – скаляр).
Это удобная форма записи, т.е. удобная модель динамической системы, использующая понятие переменных состояния zi(t). Такая модель позволяет проследить изменение во времени каждой из составляющих внутренних переменных системы и вывести условия ее управляемости и наблюдаемости (п. 2.7).
Состояние системыотделяет будущее от прошлого, содержит всю информацию о прошлом системы, необходимую для определения реакции на произвольный входной сигнал.
В общем случае n-го порядка исходного линейного ДУ можно записать векторно-матричное уравнение состояния системы
Здесь матрица А (n × n) называется матрицей объекта, а матрица В (n × m), где m – размерность вектора управления – матрицей управления. Такая форма уравнений, разрешенных относительно первых производных, называется стандартной формой.
Не всегда оказывается возможным измерить все состояния системы: z1, z2, …, zn , поэтому вводится уравнение наблюдения, которое позволяет описать, какие из состояний zi и какие из входов xi попадают в вектор наблюдаемых выходных переменныхy(t):
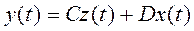
где z(t) – вектор состояния системы; x(t) – вектор управления; С–
матрица наблюдения.
Уравнение наблюдения также является линейным, причем не дифференциальным, а алгебраическим.
В рассмотренном примере 2.4.1 матрица объекта А равна:
ее размерность равна (2×2).
Матрица управления В представляет собой вектор-столбец (2×1), поскольку вектор управления x(t) в этом примере – скаляр (1×1):
Матрица наблюдения С равна единичной матрице:
а матрица D – нулевой:
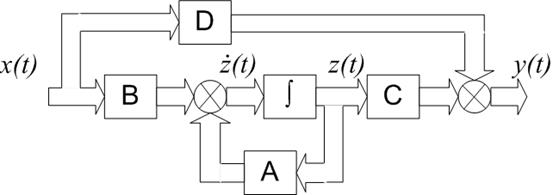
Уравнения состояния и наблюдения соответствуют структурной схеме (рис. 2.10), где матрицы A, B, C и D указаны как стационарные (с постоянными элементами), хотя в случае нестационарных линейных систем схема останется такой же. Знак ∫обозначает на схеме блок интегрирования: действительно, на входе этого блока находится производная вектора состояния, а на выходе – сам вектор состояния z(t).
Рис. 2.10. Структурная схема модели линейной стационарной системы управления в переменных состояния
Очевидно, что использование модели переменных состояния для анализа многомерных систем требует привлечения теории матриц и линейных векторных пространств.
Более подробный материал по теории матриц можно найти в Приложении 1 в конце данного пособия.
Вопросы к разделу 2.4
- Какую информацию содержит вектор состояния системы?
- Какая теорема позволяет перейти от линейного дифференциального уравнения n-го порядка к векторно-матричному уравнению состояния?
- Что описывает уравнение состояния?
- Что описывает уравнение наблюдения?
- Какова размерность матрицы объекта?
- Какова размерность матрицы управления?
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Свободное и вынужденное движение линейных систем
Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Вводные замечания
Поведение динамической системы может быть описано в виде моделей вход-выход или вход-состояние-выход [6], что соответствует линейному неоднородному дифференциальному уравнению n-го порядка или системе из п дифференциальных уравнений первого порядка соответственно. Решением дифференциальных уравнений является некоторая функция, зависящая от времени и которая содержит две составляющих [10] — общее и частное решение. В теории управления эти две составляющие принято называть свободной и вынужденной составляющими переходного процесса. Свободная составляющая определяет поведение самой динамической системы, а вынужденная — ее движение в зависимости от внешнего воздействия. Следует отметить, что для динамической системы, описанной в виде модели вход-выход, чаще всего рассчитывают параметры переходного процесса, в то время как для модели вход-состояние-выход, кроме расчета параметров, часто строят фазовые траектории.
Рассмотрим методы определения переходного процесса динамической системы, заданной дифференциальным уравнением п-го порядка.
Линейное неоднородное дифференциальное уравнения n-го порядка с постоянными коэффициентами (модель вход-выход) имеет вид [5]:
где а., Ъ. — известные коэффициенты; і = 0,l,2. n; j = 0,l,2. m; ап > 0; Ът > 0, i/(t) — имеет смысл выходного сигнала динамической системы, a u(t)— входного. В уравнении (4.1) у y(t) и u(t) зависимость от времени опущена. Решение уравнения (4.1) содержит две составляющие [1,3]:
Вынужденная составляющая yjj) соответствует переходному процессу системы (4.1) при нулевых начальных условиях y(to) = 0, у(/0) = 0. -1) (t0) = 0 и является реакцией системы на заданное входное воздействие u(t). Свободная составляющая yce(t), или переходный процесс автономной системы, соответствует решению однородного дифференциального уравнения (правая часть (4.1) или входное воздействие u(t) равны нулю):
и зависит только от начального состояния системы:
Я*о) = Уо, У(іо ) = У о ’? • ?’ = Уо
Таким образом, свободная составляющая динамической системы зависит только от параметров самой системы и от ее состояния в начальный момент 94
времени t, а вынужденная составляющая зависит только от приложенного к системе внешнего воздействия u(t). Рассмотрим методику расчета свободной и вынужденной составляющих.
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Моделирование динамических систем: численные методы решения ОДУ
Очень кратко рассмотрев основы механики в предыдущей статье, перейдем к практике, ибо даже той краткой теории что была рассмотрена хватит с головой.
Камень бросают вертикально, без начальной скорости с высоты h = 100 м. Пренебрегая сопротивлением воздуха, определить закон движения камня, как функцию высоты камня над поверхностью Земли от времени. Ускорение свободного падения принять равным 10 м/с 2
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

1. Формализация задачи
То, с чего начинается любое моделирование. Под формализацией понимают получение математических выражений, описывающих происходящий процесс. При этом формулируются допущения: перечень упрощений модели за счет факторов, влиянием которых можно пренебречь.
Для этой задачи применимо допущение, согласно которому камень можно считать материальной точкой. К этой точке приложена одна единственная сила — сила тяжести, так мы используем допущение об отсутствии сопротивления воздуха.
Следующим допущением будет полагать что Земля плоская, так как высота, с которой мы бросаем камень пренебрежимо мала в сравнении с размерами планеты, а значит кривизной её поверхности можно пренебречь. Тогда сила тяжести может считаться постоянной, направленной перпендикулярно поверхности Земли и равной по модулю
где g — ускорение свободного падения у поверхности Земли. Теперь пришло время составить уравнения движения камня. Помните эти уравнения
Левая их часть нас пока не интересует, а вот в правой стоят суммы проекций сил, приложенных к точке на оси координат. Пусть оси x и y располагаются на поверхности, а ось z направлена вверх перпендикулярно ей. Сила одна единственная, её проекции на оси x и y равны нулю, а на ось z проекция отрицательна, так как сила направлена против направления оси, то есть
Масса камня, очевидно не равна нулю, значит можно спокойно поделить обе части получившихся уравнений на неё
Не буду занудствовать, доказывая что движение камня будет происходить строго вертикально, хотя это нужно сделать с формальной точки зрения. Ноль в правой части первых двух уравнений совершенно не означает невозможность движения вдоль этих осей — вспоминаем первый закон Ньютона. На этом я остановлюсь в следующей статье более подробно, а пока справедливо положим одномерность движения, выписав окончательное дифференциальное уравнение
То что у нас получилось не много не мало — математическая модель процесса происходящего в задаче. Пафосно, да?
Нет. Анализируя это уравнение мы делаем вывод, например, что масса камня не оказывает влияния на закон его движения, ведь массы в этом уравнении нет. Видите, даже не решив уравнения, мы уже формально доказали справедливость опыта с пером и кусочком свинца в вакууме, который любят показывать в школе (а некоторые повторили его на Луне).
Аналитическое решение получить просто, даже не буду заморачиваться, оно такое
А вот как решить это численно? И что это вообще такое — «численно»?
Видео:Видеоурок "Линейные однородные диф. уравнения n-го порядка"Скачать

2. Численное интегрирование дифференциального уравнения первого порядка
Какой такой первый порядок? Я же говорил в прошлый раз, что уравнения движения имеют второй порядок. Всё правильно, но большинство методов решения диффур на компьютере умеют решать только уравнения первого порядка. Есть методы прямого интегрирования уравнений второго порядка (например метод Верле), но о них не сейчас.
Во-первых, это уравнение относится к такому типу, что допускает понижение порядка. Правая часть не зависит от неизвестной функции (там нет z), поэтому вспоминаем, что
проекция ускорения на ось z равна первой производной проекции скорости на ту же оcь z. Ну классно, тогда
вот вам и уравнение первого порядка. Не всегда этот номер проходит (не буду я сейчас про форму Коши!), но в данном случае всё в порядке. Будем искать не координату а скорость точки. Что дальше-то? А дальше
ведь производная, мы же знаем, это отношение бесконечно малого приращения функции (скорости) в к вызвавшему его бесконечно малому приращению аргумента (время). Возьмем очень маленький промежуток времени , настолько небольшой что можно считать
Что получается? А вот что
Мы получили приращение скорости. Отрицательное приращение. Как это так, камень, падая вниз будет разгонятся же! Да, будет. Его скорость, вектор его скорости, будет направлен вниз. А значит проекция этого вектора на ось z будет отрицательной. Всё правильно, мы получаем растущую по абсолютному значению проекцию вектора, направленного вниз. Мы знаем, начальное значение скорости — ноль, а значит
Пользуясь тем что мы можем вычислить приращение скорости, посчитаем, какова будет скорость скажем через 0.1 секунды
а ещё через 0.1 секунды
и ещё через 0.1 секунды
Хм, так мы можем продолжать довольно долго, но ограничимся промежутком времени в одну секунду
| Время, с | Скорость, м/с |
| 0.0 | 0.0 |
| 0.1 | -1.0 |
| 0.2 | -2.0 |
| 0.3 | -3.0 |
| 0.4 | -4.0 |
| 0.5 | -5.0 |
| 0.6 | -6.0 |
| 0.7 | -7.0 |
| 0.8 | -8.0 |
| 0.9 | -9.0 |
| 1.0 | -10.0 |
То есть, воспользовавшись формулой
мы получили зависимость скорости точки от времени. А всего-то нужно взять значение скорости в текущий момент времени, и добавить к нему приращение, которое скорость получит в новый момент времени, отстоящий от текущего на секунд. Приращение времени называется здесь шагом интегрирования. А приращение мы вычисляем как значение производной искомой функции в текущий момент времени умноженное на шаг. Просто? Да просто конечно. И та формула, которую я написал, имеет название название — явный метод Эйлера для численного решения дифференциальных уравнений. Это так называемая рекуррентная формула, когда новое значение вычисляемой величины зависит от её предыдущего значения.
А что же с высотой точки над Землей? Да всё аналогично, смотрите
ведь проекция скорости есть производная от соответствующей координаты. Применим формулу метода Эйлера для этого уравнения, ведь скорость мы уже знаем
и по этой формуле добавим в нашу таблицу ещё одну колонку
| Время, с | Скорость, м/с | Высота, м |
| 0.0 | 0.0 | 100.0 |
| 0.1 | -1.0 | 100.0 |
| 0.2 | -2.0 | 99.9 |
| 0.3 | -3.0 | 99.7 |
| 0.4 | -4.0 | 99.4 |
| 0.5 | -5.0 | 99.0 |
| 0.6 | -6.0 | 98.5 |
| 0.7 | -7.0 | 97.9 |
| 0.8 | -8.0 | 97.2 |
| 0.9 | -9.0 | 96.4 |
| 1.0 | -10.0 | 95.5 |
Хм, ну, во-первых, заметно, что высота меняется у нас уже неравномерно, так как скорость со временем меняется. Теперь наша производная сама зависит от времени. Но уже на первом шаге, мы замечаем неладное — скорость уже есть, а вот высота по прежнему 100 метров. Как так?
Это вышло потому, что на каждом шаге мы полагаем производную (скорость) постоянной. Метод не дает информации о том, что происходит с решением между шагами. Соответственно накапливается погрешность, сравним полученное решение с точным
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 100.0 | 99.95 |
| 0.2 | -2.0 | 99.9 | 99.80 |
| 0.3 | -3.0 | 99.7 | 99.55 |
| 0.4 | -4.0 | 99.4 | 99.20 |
| 0.5 | -5.0 | 99.0 | 98.75 |
| 0.6 | -6.0 | 98.5 | 98.20 |
| 0.7 | -7.0 | 97.9 | 97.55 |
| 0.8 | -8.0 | 97.2 | 96.80 |
| 0.9 | -9.0 | 96.4 | 95.95 |
| 1.0 | -10.0 | 95.5 | 95.00 |
Да, наш камень как будто зависает в воздухе. Численное решение отстает от аналитического, и чем дальше мы считаем, тем выше погрешность счета. Погрешность накапливается, так как на каждом шаге мы берем всё более и более грубое приближение. Что делать?
Во первых, можно уменьшить шаг. Скажем в 10 раз, пусть секунды
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.96 | 99.95 |
| 0.2 | -2.0 | 99.81 | 99.80 |
| 0.3 | -3.0 | 99.57 | 99.55 |
| 0.4 | -4.0 | 99.22 | 99.20 |
| 0.5 | -5.0 | 98.78 | 98.75 |
| 0.6 | -6.0 | 98.23 | 98.20 |
| 0.7 | -7.0 | 97.59 | 97.55 |
| 0.8 | -8.0 | 96.84 | 96.80 |
| 0.9 | -9.0 | 96.00 | 95.95 |
| 1.0 | -10.0 | 95.05 | 95.00 |
Уже лучше, погрешность в конце счета не превышает 0,05 метров, и это в 10 раз меньше предыдущего значения. Можно предположить, что уменьшив шаг ещё в 10 раз мы получим ещё более точное решение. Я схитрил, выводя значения только для 10 точек с шагом 0.1, на самом деле, чтобы получить такую таблицу нужны уже 100 итерации а не 10. При шаге 0.001 потребуется уже тысяча итераций, а результат будет таким
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.9505 | 99.95 |
| 0.2 | -2.0 | 99.8010 | 99.80 |
| 0.3 | -3.0 | 99.5515 | 99.55 |
| 0.4 | -4.0 | 99.2020 | 99.20 |
| 0.5 | -5.0 | 98.7525 | 98.75 |
| 0.6 | -6.0 | 98.2030 | 98.20 |
| 0.7 | -7.0 | 97.5535 | 97.55 |
| 0.8 | -8.0 | 96.8040 | 96.80 |
| 0.9 | -9.0 | 95.9545 | 95.95 |
| 1.0 | -10.0 | 95.0050 | 95.00 |
Если вы попробовали выполнить эти расчеты в ручную, то понимаете теперь насколько они однообразны и трудоемки, если нужна высокая точность. Именно поэтому расцвет численного моделирования совпал с появлением компьютеров. Они как раз и нужны для того, чтобы быстро выполнять множество однообразных операций над числами.
Метод Эйлера самый простой из известных методов интегрирования дифференциальных уравнений. Из нашего простого примера видно, что погрешность метода прямо пропорциональна шагу интегрирования, и это действительно так. Такие методы называются методами 1-го порядка точности.
Точность расчетов даже на шаге 0.1 можно улучшить, если мы применим, скажем метод Рунге-Кутты 4-го порядка точности. Но это отдельная история.
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Заключение
Задумайтесь… Мы рассмотрели очень простой пример. Мы даже не применяли компьютер, но уже понимаем принцип, по которому работают те самые мощные в мире суперкомпьютеры, что моделируют ранние этапы жизни Вселенной. Конечно, там всё устроено гораздо сложнее, но принцип лежит этот же самый.
Представьте себе, какой мощный инструмент вы получаете в свои руки. Эта последняя статья, где мы не будем применять компьютер. Я обещал Octave. В следующий раз будет именно он.
💥 Видео
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Лекция №7 "Динамические системы" (Филимонов Д. А.)Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Модели на основе дифференциальных уравнений с запаздыванием.Скачать

Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать