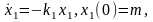Очень кратко рассмотрев основы механики в предыдущей статье, перейдем к практике, ибо даже той краткой теории что была рассмотрена хватит с головой.
Камень бросают вертикально, без начальной скорости с высоты h = 100 м. Пренебрегая сопротивлением воздуха, определить закон движения камня, как функцию высоты камня над поверхностью Земли от времени. Ускорение свободного падения принять равным 10 м/с 2
- 1. Формализация задачи
- 2. Численное интегрирование дифференциального уравнения первого порядка
- Заключение
- Математические модели динамических систем
- Просмотр содержимого документа «Математические модели динамических систем»
- Модель динамических систем дифференциальных уравнений
- Динамическая система и ее математическая модель
- Кинематическая интерпретация системы дифференциальных уравнений
- Классификация динамических систем
- Колебательные системы и их свойства
- 📺 Видео
Видео:3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать

1. Формализация задачи
То, с чего начинается любое моделирование. Под формализацией понимают получение математических выражений, описывающих происходящий процесс. При этом формулируются допущения: перечень упрощений модели за счет факторов, влиянием которых можно пренебречь.
Для этой задачи применимо допущение, согласно которому камень можно считать материальной точкой. К этой точке приложена одна единственная сила — сила тяжести, так мы используем допущение об отсутствии сопротивления воздуха.
Следующим допущением будет полагать что Земля плоская, так как высота, с которой мы бросаем камень пренебрежимо мала в сравнении с размерами планеты, а значит кривизной её поверхности можно пренебречь. Тогда сила тяжести может считаться постоянной, направленной перпендикулярно поверхности Земли и равной по модулю
где g — ускорение свободного падения у поверхности Земли. Теперь пришло время составить уравнения движения камня. Помните эти уравнения
Левая их часть нас пока не интересует, а вот в правой стоят суммы проекций сил, приложенных к точке на оси координат. Пусть оси x и y располагаются на поверхности, а ось z направлена вверх перпендикулярно ей. Сила одна единственная, её проекции на оси x и y равны нулю, а на ось z проекция отрицательна, так как сила направлена против направления оси, то есть
Масса камня, очевидно не равна нулю, значит можно спокойно поделить обе части получившихся уравнений на неё
Не буду занудствовать, доказывая что движение камня будет происходить строго вертикально, хотя это нужно сделать с формальной точки зрения. Ноль в правой части первых двух уравнений совершенно не означает невозможность движения вдоль этих осей — вспоминаем первый закон Ньютона. На этом я остановлюсь в следующей статье более подробно, а пока справедливо положим одномерность движения, выписав окончательное дифференциальное уравнение
То что у нас получилось не много не мало — математическая модель процесса происходящего в задаче. Пафосно, да?
Нет. Анализируя это уравнение мы делаем вывод, например, что масса камня не оказывает влияния на закон его движения, ведь массы в этом уравнении нет. Видите, даже не решив уравнения, мы уже формально доказали справедливость опыта с пером и кусочком свинца в вакууме, который любят показывать в школе (а некоторые повторили его на Луне).
Аналитическое решение получить просто, даже не буду заморачиваться, оно такое
А вот как решить это численно? И что это вообще такое — «численно»?
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

2. Численное интегрирование дифференциального уравнения первого порядка
Какой такой первый порядок? Я же говорил в прошлый раз, что уравнения движения имеют второй порядок. Всё правильно, но большинство методов решения диффур на компьютере умеют решать только уравнения первого порядка. Есть методы прямого интегрирования уравнений второго порядка (например метод Верле), но о них не сейчас.
Во-первых, это уравнение относится к такому типу, что допускает понижение порядка. Правая часть не зависит от неизвестной функции (там нет z), поэтому вспоминаем, что
проекция ускорения на ось z равна первой производной проекции скорости на ту же оcь z. Ну классно, тогда
вот вам и уравнение первого порядка. Не всегда этот номер проходит (не буду я сейчас про форму Коши!), но в данном случае всё в порядке. Будем искать не координату а скорость точки. Что дальше-то? А дальше
ведь производная, мы же знаем, это отношение бесконечно малого приращения функции (скорости) в к вызвавшему его бесконечно малому приращению аргумента (время). Возьмем очень маленький промежуток времени , настолько небольшой что можно считать
Что получается? А вот что
Мы получили приращение скорости. Отрицательное приращение. Как это так, камень, падая вниз будет разгонятся же! Да, будет. Его скорость, вектор его скорости, будет направлен вниз. А значит проекция этого вектора на ось z будет отрицательной. Всё правильно, мы получаем растущую по абсолютному значению проекцию вектора, направленного вниз. Мы знаем, начальное значение скорости — ноль, а значит
Пользуясь тем что мы можем вычислить приращение скорости, посчитаем, какова будет скорость скажем через 0.1 секунды
а ещё через 0.1 секунды
и ещё через 0.1 секунды
Хм, так мы можем продолжать довольно долго, но ограничимся промежутком времени в одну секунду
| Время, с | Скорость, м/с |
| 0.0 | 0.0 |
| 0.1 | -1.0 |
| 0.2 | -2.0 |
| 0.3 | -3.0 |
| 0.4 | -4.0 |
| 0.5 | -5.0 |
| 0.6 | -6.0 |
| 0.7 | -7.0 |
| 0.8 | -8.0 |
| 0.9 | -9.0 |
| 1.0 | -10.0 |
То есть, воспользовавшись формулой
мы получили зависимость скорости точки от времени. А всего-то нужно взять значение скорости в текущий момент времени, и добавить к нему приращение, которое скорость получит в новый момент времени, отстоящий от текущего на секунд. Приращение времени называется здесь шагом интегрирования. А приращение мы вычисляем как значение производной искомой функции в текущий момент времени умноженное на шаг. Просто? Да просто конечно. И та формула, которую я написал, имеет название название — явный метод Эйлера для численного решения дифференциальных уравнений. Это так называемая рекуррентная формула, когда новое значение вычисляемой величины зависит от её предыдущего значения.
А что же с высотой точки над Землей? Да всё аналогично, смотрите
ведь проекция скорости есть производная от соответствующей координаты. Применим формулу метода Эйлера для этого уравнения, ведь скорость мы уже знаем
и по этой формуле добавим в нашу таблицу ещё одну колонку
| Время, с | Скорость, м/с | Высота, м |
| 0.0 | 0.0 | 100.0 |
| 0.1 | -1.0 | 100.0 |
| 0.2 | -2.0 | 99.9 |
| 0.3 | -3.0 | 99.7 |
| 0.4 | -4.0 | 99.4 |
| 0.5 | -5.0 | 99.0 |
| 0.6 | -6.0 | 98.5 |
| 0.7 | -7.0 | 97.9 |
| 0.8 | -8.0 | 97.2 |
| 0.9 | -9.0 | 96.4 |
| 1.0 | -10.0 | 95.5 |
Хм, ну, во-первых, заметно, что высота меняется у нас уже неравномерно, так как скорость со временем меняется. Теперь наша производная сама зависит от времени. Но уже на первом шаге, мы замечаем неладное — скорость уже есть, а вот высота по прежнему 100 метров. Как так?
Это вышло потому, что на каждом шаге мы полагаем производную (скорость) постоянной. Метод не дает информации о том, что происходит с решением между шагами. Соответственно накапливается погрешность, сравним полученное решение с точным
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 100.0 | 99.95 |
| 0.2 | -2.0 | 99.9 | 99.80 |
| 0.3 | -3.0 | 99.7 | 99.55 |
| 0.4 | -4.0 | 99.4 | 99.20 |
| 0.5 | -5.0 | 99.0 | 98.75 |
| 0.6 | -6.0 | 98.5 | 98.20 |
| 0.7 | -7.0 | 97.9 | 97.55 |
| 0.8 | -8.0 | 97.2 | 96.80 |
| 0.9 | -9.0 | 96.4 | 95.95 |
| 1.0 | -10.0 | 95.5 | 95.00 |
Да, наш камень как будто зависает в воздухе. Численное решение отстает от аналитического, и чем дальше мы считаем, тем выше погрешность счета. Погрешность накапливается, так как на каждом шаге мы берем всё более и более грубое приближение. Что делать?
Во первых, можно уменьшить шаг. Скажем в 10 раз, пусть секунды
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.96 | 99.95 |
| 0.2 | -2.0 | 99.81 | 99.80 |
| 0.3 | -3.0 | 99.57 | 99.55 |
| 0.4 | -4.0 | 99.22 | 99.20 |
| 0.5 | -5.0 | 98.78 | 98.75 |
| 0.6 | -6.0 | 98.23 | 98.20 |
| 0.7 | -7.0 | 97.59 | 97.55 |
| 0.8 | -8.0 | 96.84 | 96.80 |
| 0.9 | -9.0 | 96.00 | 95.95 |
| 1.0 | -10.0 | 95.05 | 95.00 |
Уже лучше, погрешность в конце счета не превышает 0,05 метров, и это в 10 раз меньше предыдущего значения. Можно предположить, что уменьшив шаг ещё в 10 раз мы получим ещё более точное решение. Я схитрил, выводя значения только для 10 точек с шагом 0.1, на самом деле, чтобы получить такую таблицу нужны уже 100 итерации а не 10. При шаге 0.001 потребуется уже тысяча итераций, а результат будет таким
| Время, с | Скорость, м/с | Высота, м | Точное решение, м |
| 0.0 | 0.0 | 100.0 | 100.00 |
| 0.1 | -1.0 | 99.9505 | 99.95 |
| 0.2 | -2.0 | 99.8010 | 99.80 |
| 0.3 | -3.0 | 99.5515 | 99.55 |
| 0.4 | -4.0 | 99.2020 | 99.20 |
| 0.5 | -5.0 | 98.7525 | 98.75 |
| 0.6 | -6.0 | 98.2030 | 98.20 |
| 0.7 | -7.0 | 97.5535 | 97.55 |
| 0.8 | -8.0 | 96.8040 | 96.80 |
| 0.9 | -9.0 | 95.9545 | 95.95 |
| 1.0 | -10.0 | 95.0050 | 95.00 |
Если вы попробовали выполнить эти расчеты в ручную, то понимаете теперь насколько они однообразны и трудоемки, если нужна высокая точность. Именно поэтому расцвет численного моделирования совпал с появлением компьютеров. Они как раз и нужны для того, чтобы быстро выполнять множество однообразных операций над числами.
Метод Эйлера самый простой из известных методов интегрирования дифференциальных уравнений. Из нашего простого примера видно, что погрешность метода прямо пропорциональна шагу интегрирования, и это действительно так. Такие методы называются методами 1-го порядка точности.
Точность расчетов даже на шаге 0.1 можно улучшить, если мы применим, скажем метод Рунге-Кутты 4-го порядка точности. Но это отдельная история.
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Заключение
Задумайтесь… Мы рассмотрели очень простой пример. Мы даже не применяли компьютер, но уже понимаем принцип, по которому работают те самые мощные в мире суперкомпьютеры, что моделируют ранние этапы жизни Вселенной. Конечно, там всё устроено гораздо сложнее, но принцип лежит этот же самый.
Представьте себе, какой мощный инструмент вы получаете в свои руки. Эта последняя статья, где мы не будем применять компьютер. Я обещал Octave. В следующий раз будет именно он.
Видео:Моделирование на основе дифференциальных уравненийСкачать

Математические модели динамических систем
Просмотр содержимого документа
«Математические модели динамических систем»
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ СИСТЕМ
Первоначально термин «динамическая система» применялся в основном к механическим системам, движение которых описывается дифференциальными уравнениями. Основные результаты о динамических системах были получены А.М. Ляпуновым и А. Пуанкаре в конце девятнадцатого века. Позднее стало очевидно, что понятие динамических систем полезно для анализа различных эволюционных процессов, изучаемых во многих науках. Определение динамической системы является математической формализацией общей научной концепции детерминированного процесса. Процесс называется детерминированным, если весь его будущий ход и все его прошлое однозначно определяются состоянием в настоящее время.
Будущее состояние многих физических, биологических, экологических и даже общественных систем может быть предсказано в некоторых пределах, если известно настоящее состояние и закон, управляющей их эволюцией.
Широкий круг явлений природы, а также многие технические объекты могут быть описаны дифференциальными уравнениями. Они являются естественным языком для описания разнообразных динамических систем, таких как движение планет Солнечной системы, процесс образования волн на море, функционирование атомных станций, систем автоматического управления космическими кораблями и т. д. Поэтому математические модели в виде дифференциальных уравнений играют важную роль в теории моделирования.
1. Классификация дифференциальных уравнений
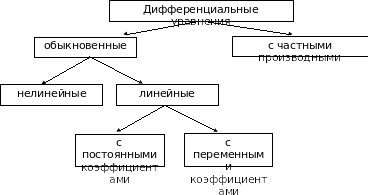
Дифференциальные уравнения представляют собой соотношения, связывающие переменные и их производные. По количеству независимых переменных дифференциальные уравнения делятся на два больших класса: обыкновенные дифференциальные уравнения и дифференциальные уравнения с частными производными.
Рис. 1.1. Классификация дифференциальных уравнений
К первому классу относятся уравнения, в которых имеется только одна независимая переменная, например время. В уравнения второго класса входят несколько независимых переменных, например время и пространственные координаты. Как правило, решать эти уравнения значительно труднее.
Общая запись обыкновенного дифференциального уравнения имеет вид
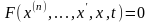
Наивысший порядок входящей в него производной называется порядком уравнения.
Дифференциальное уравнение называется линейным, если функция F линейна, и нелинейным – в противном случае. Простейшими примерами могут служить уравнения 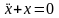
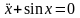
Если коэффициенты линейного дифференциального уравнения зависят от времени, то говорят о линейном уравнении с переменными коэффициентами. В тех случаях, когда коэффициенты постоянные, уравнение называется стационарным, или уравнением с постоянными коэффициентами. Классификация дифференциальных уравнений по перечисленным признакам приведена на рис. 1.1.
Для линейных дифференциальных уравнений разработаны аналитические методы их решения. теория нелинейных дифференциальных уравнений развита значительно хуже. общих методов решения таких уравнений не существует, описаны лишь отдельные типы уравнений, которые могут быть проинтегрированы, такие как уравнения Бернулли, Риккати и др. При компьютерном моделировании, как правило, ограничиваются получением численного решения, отвечающего конкретным значениям параметров. оно выводится в виде графика или соответствующего массива числовых данных.
2. Построение математических моделей динамических систем
Первый шаг при моделировании динамических систем состоит в переходе от физической или технической задачи к ее математической модели в виде дифференциального уравнения или системы таких уравнений. При этом используются теория и законы соответствующей предметной области, например, при моделировании механических систем это законы ньютона и сохранения энергии; при моделировании электрических схем – законы Ома и Кирхгофа и т. п. Поясним процедуру построения математической модели динамических систем на нескольких примерах.
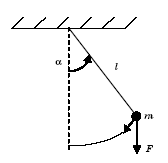
Пример 1.1. Математический маятник. Рассмотрим маятник массы т и длины l, который совершает малые колебания около положения равновесия (pис. 1.2). Требуется найти дифференциальное уравнение, описывающее колебания этой механической системы.
Рис. 1.2. Математический маятник
Для построения математической модели воспользуемся формулой второго закона Ньютона F = та, где F – сила, действующая на материальную точку вдоль касательной к траектории; 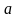
Обозначим угловое отклонение маятника α(t), тогда
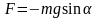
Линейное ускорение 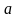
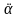
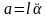
Подставляя эти выражения в уравнение 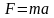
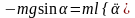
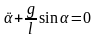
Это нелинейное дифференциальное уравнение второго порядка.
В случае малых колебаний замена 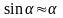
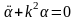
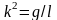
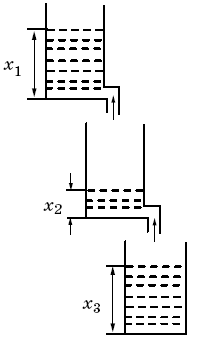
Пример 1.2. Резервуары с жидкостью. Рассмотрим задачу о протекании жидкости через три сообщающихся сосуда (рис. 1.3). Обозначим уровни жидкости в сосудах через x1(t), x2(t), x3(t) и будем считать, что в начальный момент времени жидкость была только в первом сосуде, т. е. х1(0) = m, х2 (0) = х3(0) = 0. Очевидно, что с течением времени х1 будет убывать, а х3 – возрастать. Уровень х2 сначала будет расти, а затем, начиная с некоторого момента времени t1, уменьшаться.
Рис.1.3. Три резервуара
Полагая скорость вытекания жидкости пропорциональной ее количеству, получаем, что процесс может быть описан системой трех дифференциальных уравнений
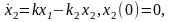
Левые части уравнений (1.2) соответствуют скоростям изменения уровней жидкости в сосудах, положительные и отрицательные слагаемые в правых частях уравнений характеризуют количество прироста и убыли жидкости. например, слагаемое k1х1 во втором уравнении отражает приток жидкости во второй сосуд из первого, а слагаемое –k2х2 отражает ее вытекание из второго сосуда в третий.
Уравнения (1.2) можно переписать в матричной форме
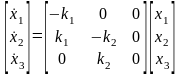
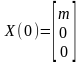
Эту модель можно усложнить, учитывая возможность пополнения жидкости в первом сосуде и вытекания ее из третьего сосуда.
Пример 1.3. Система «загрязнение-окружающая среда». Пусть рассматривается замкнутая система загрязнение – природа. В первом приближении состояние этой системы можно описать парой чисел 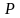
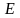
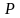
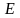
Предположим, что имеется постоянный источник загрязнения. Загрязнение отрицательно влияет на окружающую среду. Пусть окружающая среда способна перерабатывать загрязнение до определенного предела. Тогда динамика системы загрязнение – окружающая среда можно описать следующей системой обыкновенных дифференциальных уравнений:
где 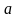
Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Модель динамических систем дифференциальных уравнений
Одной из важных научных проблем естествознания является решение задачи предсказания поведения изучаемого объекта во времени и пространстве на основе определенных знаний о его начальном состоянии. Эта задача сводится к нахождению некоторого закона, который позволяет по имеющейся информации об объекте в начальный момент времени t0 в точке пространства x0 определить его будущее в любой момент времени t > t0. В зависимости от степени сложности самого объекта этот закон может быть детерминированным или вероятностным , может описывать эволюцию объекта только во времени, только в пространстве, а может описывать пространственно-временную эволюцию.
Предметом нашего анализа будут не объекты вообще, а динамические системы в математическом понимании этого термина [1].
Динамическая система и ее математическая модель
Под динамической системой понимают любой объект или процесс, для которого однозначно определено понятие состояния как совокупности некоторых величин в данный момент времени и задан закон, который описывает изменение (эволюцию) начального состояния с течением времени. Этот закон позволяет по начальному состоянию прогнозировать будущее состояние динамической системы, его называют законом эволюции. Динамические системы — это механические, физические, химические и биологические объекты, вычислительные процессы и процессы преобразования информации, совершаемые в соответствии с конкретными алгоритмами. Описания динамических систем для задания закона эволюции также разнообразны: с помощью дифференциальных уравнений , дискретных отображений, теории графов, теории марковских цепей и т.д. Выбор одного из способов описания задает конкретный вид математической модели соответствующей динамической системы [2].
Математическая модель динамической системы считается заданной, если введены параметры (координаты) системы, определяющие однозначно ее состояние, и указан закон эволюции. В зависимости от степени приближения одной и той же системе могут быть поставлены в соответствие различные математические модели.
Исследование реальных систем сводится к изучению математических моделей, совершенствование и развитие которых определяются анализом экспериментальных и теоретических результатов при их сопоставлении. В связи с этим под динамической системой мы будем понимать именно ее математическую модель. Исследуя одну и ту же динамическую систему (к примеру, движение маятника), в зависимости от степени учета различных факторов мы получим различные математические модели. В качестве примера рассмотрим модель нелинейного консервативного осциллятора:
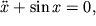
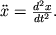
Как известно, функция 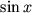
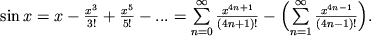
При малых 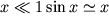
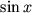
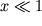
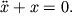
Следующим приближением будет модель нелинейного маятника :
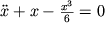
и т.д. Для каждого конкретного значения n будем получать новую динамическую систему, в заданном приближении описывающую процесс колебаний физического маятника .
Кинематическая интерпретация системы дифференциальных уравнений
Рассмотрим динамические системы, моделируемые конечным числом обыкновенных дифференциальных уравнений . Применительно к таким системам сохранились представления и терминология, первоначально возникшие в механике. В рассматриваемом случае для определения динамической системы необходимо указать объект, допускающий описание состояния заданием величин x1, x2, . xN в некоторый момент времени t = t0. Величины xi могут принимать произвольные значения, причем двум различным наборам величин xi и 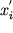
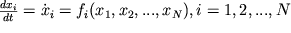
Если рассматривать величины x1, x2, . xN как координаты точки x в N-мерном пространстве, то получается наглядное геометрическое представление состояния динамической системы в виде этой точки, которую называют изображающей, а чаще фазовой точкой, а пространство состояний — фазовым пространством динамической системы. Изменению состояния системы во времени отвечает движение фазовой точки вдоль некоторой линии, называемой фазовой траекторией. В фазовом пространстве системы уравнениями (5) определяется векторное поле скоростей, сопоставляющее каждой точке x выходящий из нее вектор скорости F(x), компоненты которого даются правыми частями уравнений (5):
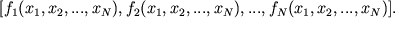
Динамическая система (5) может быть записана в векторной форме:
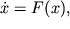
Необходимо уточнить взаимосвязь понятий числа степеней свободы и размерности фазового пространства динамической системы. Под числом степеней свободы понимается наименьшее число независимых координат, необходимых для однозначного определения состояния системы. Под координатами первоначально понимались именно пространственные переменные, характеризующие взаимное расположение тел и объектов. В то же время для однозначного решения соответствующих уравнений движения необходимо помимо координат задать соответствующие начальные значения импульсов или скоростей. В связи с этим система с n степенями свободы характеризуется фазовым пространством в два раза большей размерности (N = 2n).
Классификация динамических систем
Если динамическая система задана уравнением (7), то постулируется, что каждому x(t0) в фазовом пространстве ставится в соответствие состояние x(t), t > t0, куда за время t — t0 переместится фазовая точка, движущаяся в соответствии с уравнением (7). В операторной форме (7) можно записать в виде [2]
где Tt — закон (оператор) эволюции. Если этот оператор применить к начальному состоянию x(t0), то мы получим x(t), то есть состояние в момент времени t > t0. Так как x(t0) и x(t) принадлежат одному и тому же фазовому пространству динамической системы, то математики говорят в данной ситуации: оператор Tt отображает фазовое пространство системы на себя. В соответствии с этим можно называть оператор Tt оператором отображения или просто отображением.
Динамические системы можно классифицировать в зависимости от вида оператора отображения и структуры фазового пространства. Если оператор предусматривает исключительно линейные преобразования начального состояния, то он называется линейным. Линейный оператор обладает свойством суперпозиции: T[x(t) + y(t)] = Tx(t) + Ty(t). Если оператор нелинейный, то и соответствующая динамическая система называется нелинейной. Различают непрерывные и дискретные операторы и соответственно системы с непрерывным и дискретным временем. Системы, для которых отображение x(t) с помощью оператора T может быть определено для любых t > t0 (непрерывно во времени), называют также потоками по аналогии со стационарным течением жидкости . Если оператор отображения определен на дискретном множестве значений времени, то соответствующие динамические системы называют каскадами или системами с дискретным временем.
Способы задания оператора отображения T также могут различаться. Оператор T можно задать в виде дифференциального или интегрального преобразования, в виде матрицы или таблицы, в виде графика или функции и т.д.
Колебательные системы и их свойства
Важную группу динамических систем представляют системы, в которых возможны колебания. Колебательные системы с точки зрения их математических моделей разделяют на определенные классы. Различают линейные и нелинейные колебательные системы, сосредоточенные и распределенные, консервативные и диссипативные, автономные и неавтономные. Особый класс представляют так называемые автоколебательные системы. Основные свойства указанных систем подробно обсуждаются в работах по теории колебаний.
📺 Видео
Модели на основе дифференциальных уравнений с запаздыванием.Скачать

Модели, представленный системой двух дифференциальных уравненийСкачать

Модели биологических систем, описываемые одним дифференциальным уравнением первого порядкаСкачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Обыкновенные дифференциальные уравнения - 01 - Модель экспоненциального ростаСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения. 11 класс.Скачать

Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать

1.1. Составление имитационной модели в виде дифференциального уравненияСкачать