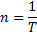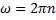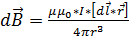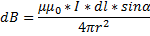Модель абсолютно упругого тела уравнение (8 видео)

Содержание

Модели в механике: материальная точка, системы материальных точек, абсолютно твёрдое тело, абсолютно упругое тело, абсолютно неупругое тело.
Упругие и неупругие соударения
Абсолютно неупругий удар. Скорость
Абсолютно упругий удар
Предельное расстояние
Столкновение тел. Абсолютно упругий и абсолютно неупругий удары
🔍 Видео

Видео:Урок 128. Соударения телСкачать

Модели в механике: материальная точка, системы материальных точек, абсолютно твёрдое тело, абсолютно упругое тело, абсолютно неупругое тело.

Физика. Ответы.

Модели в механике: материальная точка, системы материальных точек, абсолютно твёрдое тело, абсолютно упругое тело, абсолютно неупругое тело.

Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.

Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Абсолютно твёрдое тело – тело, которое ни при каких условиях никогда не деформируется.

Абсолютно упругое тело – тело, которое подвергается деформации под действием некоторых сил, но после прекращения действия сил форма тела полностью восстанавливается.

Абсолютно неупругое тело – тело, которое деформируется под действием некоторых сил, и после прекращения действия сил форма не восстанавливается.

Механическое движение. Тело отсчёта, система отсчёта, уравнение движения материальной точки, траектория движения, путь и перемещение.

Механическое движение —изменение положения тела в пространстве относительно других тел с течением времени.

Тело отсчёта – произвольно выбранное тело, относительно которого определяется положение других тел.

Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.

Уравнение движения, описывающее положение материальной точки, можно записать в векторном виде или координатной форме:

Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называетсядлиной пути Δ S и являетсяскалярной функцией времени: Δ s = Δ s(t). Вектор Δ r=r-r₀, проведенный из начального положения движущейся точки в положение ее в. данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

Траектория движения – линия, вдоль которой тело движется с течением времени.

Путь – длина траектории.

Вращательное движение твёрдого тела, угловая и линейная скорость, связь линейной скорости с угловой, период вращения, угловое ускорение, направление угловой скорости и ускорения.

Тело может двигаться не только по прямой, но и по окружности.

Вращательное движение – движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени

Линейной скоростью называется скорость, с которой точка движется по окружности.

n – частота, число оборотов, совершаемое телом за единицу времени.

Момент инерции. Момент инерции материальной точки. Моменты инерции однородных тел. Момент силы относительно неподвижной оси. Плечо силы.

Момент инерции системы или тела относительно оси вращения есть физическая величина, численно равная произведению массы тела на квадрат расстояния материальной точки относительно вершины.

Моментом инерции материальной точки относительно некоторой оси вращения называется физическая величина, численно равная произведению массы этой точки на квадрат расстояния от нее до оси вращения.

Закон сохранения заряда

Алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах.

В замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Одним из способов получения заряда – использование трения

Закон Кулона

Сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, прямо пропорциональна произведению модулей зарядов, обратно пропорциональна квадрату расстояния между ними.

= 9*10^9 (Hm²/Кл)

Ɛо = 8,85 * 10^-2 (ф/м) фарады

Система СГС (сантиметр, грамм, секунда)

F = (1÷4П*Ɛо*Ɛ)*(q*qо÷r²) – среда

Ɛ – диэлектрическая проницаемость – показывает во сколько раз сила взаимодействия между зарядами в среде меньше чем вакууме.

r(вектор)÷r – направлена как сила взаимодействия.

Линии напряженности

Силовая линия напряженности – силовой линией называется тонкая линия касательно которой каждая точка будет совпадать с электронапряженностью.

По модулю равны, но неравны по знаку.

Принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов. В качестве примера применения принципа суперпозиции полей на рис. изображена картина силовых линий поля электрического диполя

Линии на рисунке – l(вектор) – плечо, диполь

p – момент диполя

геометрическая пл. множ. точек

Дипольный момент — векторная физическая величина, характеризующая электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей.

Простейшая система зарядов, имеющая ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда н а расстояние между зарядами и направлен от отрицательного заряда к положительному, или:

p= q*l, где — величина положительного заряда, — вектор с началом в отрицательном заряде и концом в положительном. Во внешнем электрическом поле на электрический диполь действует момент сил

который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.

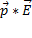
Потенциальная энергия заряда. Потенциал. Потенциал для точечного заряда. Работа перемещения заряда в поле. Разность потенциалов. Принцип суперпозиции электростатических полей. Эквипотенциальные поверхности.

Потенциальная энергия заряда qо в поле заряда q равна

U = (1/4п*Ɛо)*(q*qo/r)+C; С – произвольная постоянная

Потенциальная энергия заряда qo находящегося в поле заряда q на расстоянии r от него, равна

Для одноименных зарядов qqo>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов qqo [A]=Кл*В; 1эВ=1,6* *1В=1,6* Дж

Электронная эмиссия — явление испускания электронов с поверхности металла. Чтобы эмиссия наблюдалась электрону надо дать дополнительную энергию: нагреть металл(электроны начинают двигаться быстрее и достигают такой скорости, что вылетают с поверхности) — термоэлектронная эмиссия; фотоэмиссия — поверхность металла облучается с помощью какого-то излучения — света, например(осветить цинковую пластинку, она будет терять электроны); если на какое-то вещество направить поток электронов, то он при соприкосновении с поверхностью, сможет выбить с поверхности вторичные электроны — вторичная электронная эмиссия; можно вызвать эмиссию путем помещения металлов в сильном электрическом поле — Автоэлектронная эмиссия.

Электрический ток в газах.

Воздух является плохим проводником, поэтому тока между пластинами нет. Внесём в пространство между пластинами пламя спиртовой горелки, тогда сразу появится ток. Пламя способствует прогреванию воздуха, некоторые атомы теряют свои электроны. Процесс распада атома на отрицательный электрон и положительный ион — ионизация. Процесс образования нового нейтрального атома из электрона и положительного иона — рекомбинация.

Т.о. ток в газа — направленное движение положительных и отрицательных ионов и электронов.

Iнас. — ток насыщения. При увеличении напряжения, растет и скорость ионов и электронов, они успевают дойти до своей платины. Сколько ионизацией электронов и ионов создано, столько и использовано, поэтому ток насыщения.

Если между пластинами поместить вторую спиртовку, то ток снова будет расти, I, и U повысятся. Все частицы, которые движутся постепенно увеличат скорость, они ударяются о молекулы воздуха и происходит ударная ионизация, образуется ещё больше электронов и ионов.

Газовый разряд — эл. ток в газах. Для того чтобы ток в газах имел место, нужен ионизатор. Роль ионизатора — пламя, излучение, нагрев. Разряд газа в отсутствии ионизатора — самостоятельный, а в присутствии — несамостоятельный.

Типы самостоятельного разряда.

1. Тлеющий разряд, он происходит при низком давлении воздуха. Образуется при определенном напряжении — напряжении зажигания.

2. Искровой разряд. Это пробой воздуха. Должно быть большое количество заряда. Например, молния.

3. Коронный разряд — это самостоятельный газовый разряд, возникающий в резко неоднородных полях у электродов с большой кривизной поверхности (острия, тонкие провода). Свечение газа, которое возникает около проводников, находящихся под очень высоким напряжением.

4. Дуговой разряд. Самостоятельный газовый разряд, который характеризуется большой силой тока (десятки и сотни ампер) и малым напряжением между электродами (несколько десятков вольт). Можно получить минуя стадию искры — два электрода сводят да соприкосновения, они раскаляются эл. током, потом их разводят и получают дугу. Например, сварка металлов.

Опыт Эрстеда.

Датский ученый Эрстед в 1820 году догадался рядом с проводников, в котором течет ток, поместить магнитную стрелку. Но если включить ток, то стрелка поворачивалась на некоторый угол, а если поменять направление тока, то и стрелка меняла своё направление на 180 градусов. Результаты опыта дают основание сделать вывод, что между магнитным и электрическим полем существует определённая связь; что электрический ток создаёт поле, которое впоследствии названо магнитным. Если вблизи проводника выбрать произвольную точку, то для данной точки поля будет выполняться следующее соотношение , как бы ни менялась величина тока, длина проводника = const для данной точки и эта величина — характеристика поля для данной точки — магнитная индукция.

Магни́тная инду́кция— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства.

Картонка, в которой проделано отверстие, через него проходит провод с током; а на картонке железные опилки. Они выстраиваются в круги. Каждая частичка опилок может рассматриваться здесь, как маленький магнит, и при помещении на картонку они выстраиваются по магнитным силовым линиям.

Магнитные силовые линии — такие линии, касательные к которым в каждой точке совпадают с вектором магнитной индукции.

Для определения направления вектора магнитной индукции применяется правило буравчика: если поступательное движение буравчика совпадает с направлением тока в проводнике, то направление вращания рукоятки буравчика, совпадает с направлением вектора магнитной индукции.

Закон Био-Савара -Лапласа

Для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB:

В векторной форме

Здесь I – ток; 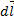– вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток; – радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем ; r – модуль радиус-вектора; магнитная проницаемость; — магнитная постоянная.

В скалярной форме

Этот закон позволяет получить формулу для расчета магнитной индукции.

Ход лучей в линзах

Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми или перевернутыми, действительными или мнимыми, увеличенными или уменьшенными.

Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей (замечательных лучей), ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Построение изображения в тонкой линзе:

1. Луч, параллельный главной оптической оси, проходит через точку главного фокуса.

2. Луч, параллельный побочной оптической оси, проходит через побочный фокус (точку на побочной оптической оси).

3. Луч, проходящий через оптический центр линзы, не преломляется.

4. Действительное изображение — пересечение лучей. Мнимое изображение — пересечение продолжений лучей

Собирающая линза

1. Если предмет располагается за двойным фокусом.

Чтобы построить изображение предмета, нужно пустить два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы, он пройдет, не преломившись. На пересечении двух лучей ставим точку А’. Это и будет изображение верхней точки предмета. Точно так же строится изображение нижней точки предмета. В результате построения получается уменьшенное, перевернутое, действительное изображение.

2.Если предмет располагается в точке двойного фокуса.

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы, он пройдет через линзу, не преломившись. На пересечении двух лучей ставим точку А1. Это и будет изображение верхней точки предмета. Точно так же строится изображение нижней точки предмета. В результате построения получается изображение, высота которого совпадает с высотой предмета. Изображение является перевернутым и действительным

3. Если предмет располагается в пространстве между фокусом и двойным фокусом

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы. Через линзу он проходит, не преломившись. На пересечении двух лучей ставим точку А’. Это и будет изображение верхней точки предмета. Точно так же строится изображение нижней точки предмета. В результате построения получается увеличенное, перевернутое, действительное изображение

Рассеивающая линза

Предмет располагается перед рассеивающей линзой.

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется таким образом, что продолжение этого луча пойдет в фокус. А второй луч, который проходит через оптический центр, пересекает продолжение первого луча в точке А’, – это и будет изображение верхней точки предмета.Таким же образом строится изображение нижней точки предмета. В результате получается прямое, уменьшенное, мнимое изображение. При перемещении предмета относительно рассеивающей линзы всегда получается прямое, уменьшенное, мнимое изображение. При перемещении предмета относительно рассеивающей линзы всегда получается прямое, уменьшенное, мнимое изображение.

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью

формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величины d и f также подчиняются определенному правилу знаков: d > 0 и f > 0 – для действительных предметов

(то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений; d

Последнее изменение этой страницы: 2017-03-14; Просмотров: 862; Нарушение авторского права страницы

Видео:ПРОСТО О СЛОЖНОМ — Деформация и Закон Гука / ФизикаСкачать

Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.

Применение такого вида задач используется в технике и физике элементарных частиц.

Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.

При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.

Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.

Видео:10. Соударение тел. Абсолютно упругий и неупругий ударСкачать

Абсолютно неупругий удар. Скорость

Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.

Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.

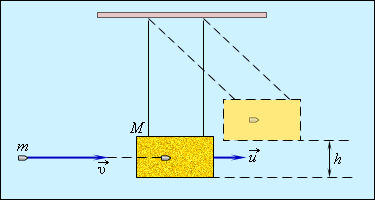
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1 . 21 . 1 , m – горизонтально летящая пуля с v → скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.

Если скорость ящика с пулей обозначить как u → , тогда, используя формулу сохранения импульса, получаем:

m v = ( M + m ) u ; u = m M + m v .

Когда пуля застревает в песке, то механическая энергия теряется:

∆ E = m v 2 2 — ( M + m ) u 2 2 = M M + m · m v 2 2 .

M ( M + m ) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда

∆ E E 0 = M M + m = 1 1 + m M .

Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.

Когда m М ∆ E E 0 → 1 2 , тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆ E E 0 → 0 , только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим ( m > > М ) , отношение принимает вид ∆ E E 0 → 0 .

Расчет движения маятника производится по закону сохранения механической энергии. Получаем

( M + m ) u 2 2 = ( M + m ) g h ; u 2 = 2 g h .

В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что

v = M + m m 2 g h .

При известной высоте h возможно определение скорости пули v .

Рисунок 1 . 21 . 1 . Баллистический маятник.

Видео:Урок 129. Частные случаи абсолютно упругого центрального соударенияСкачать

Абсолютно упругий удар

Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.

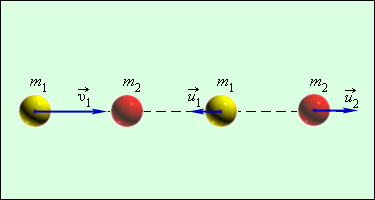
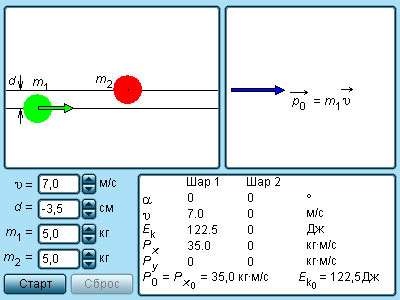
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1 . 21 . 2 .

Центральный удар – это соударение, когда скорости шаров направлены по линии центра.

Рисунок 1 . 21 . 2 . Абсолютно упругий центральный удар шаров.

Встречаются случаи, когда массы m 1 и m 2 не равны. Тогда, используя закон сохранения механической энергии, получаем

m 1 v 1 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 .

За v 1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v 2 = 0 скорость второго шара, u 1 и u 2 – скорости после столкновения.

Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:

m 1 v 1 = m 1 u 1 + m 2 u 2 .

Полученная система из двух уравнений позволяет найти неизвестные скорости u 1 и u 2 шаров после столкновения.

u 1 = m 1 — m 2 v 1 m 1 + m 2 ; u 2 = 2 m 1 v 1 m 1 + m 2 .

Если массы равны, то есть, тогда происходит остановка первого шара ( u 1 = 0 ) , а второй продолжает движение u 2 = v 1 _. происходит обмен скоростями и импульсами.

При наличии нулевой скорости второго шара ( v 2 ≠ 0 ) , задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v 2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v 1 ‘ = v 1 – v 2 _. После определения скорости шаров v 1 и v 2 производится переход к «неподвижной» системе.

С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.

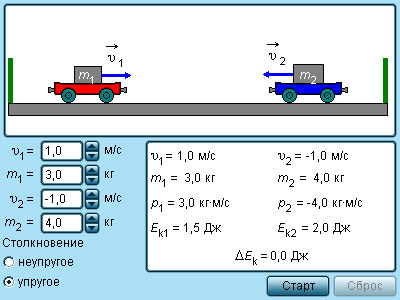
Рисунок 1 . 21 . 3 . Модель упругие и неупругие соударения.

При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.

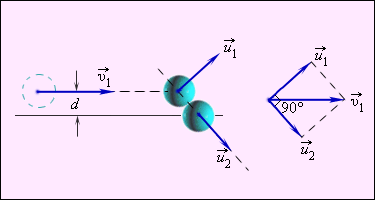
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1 . 21 . 4 .

Рисунок 1 . 21 . 4 . Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.

Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v 1 и v 2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d , изображенное на рисунке 1 . 21 . 4 .

Видео:Лекция II-4. Математические модели твердого телаСкачать

Предельное расстояние

Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v 1 → летящего шара.

При одинаковых массах шаров векторы v 1 → и v 2 → имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m 1 = m 2 = m , тогда определение примет вид

v 1 → = u 1 → + u 2 → ; v 1 2 = u 1 2 + u 2 2 .

Первое равенство значит, что векторы v 1 → , u 1 → , u 2 → образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u 1 → и u 2 → , равняется 90 градусов.

Рисунок 1 . 21 . 5 . Модель соударения упругих шаров

Видео:Абсолютно упругий и неупругий удар. ЕГЭ по физике 2023Скачать

Столкновение тел. Абсолютно упругий и абсолютно неупругий удары

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы продолжаем изучать законы сохранения и рассмотрим различные возможные удары тел. Из своего опыта вы знаете, что накачанный баскетбольный мяч хорошо отскакивает от пола, тогда как сдутый – практически не отскакивает. Из этого вы могли сделать вывод, что удары различных тел могут быть разными. Для того чтобы охарактеризовать удары, вводятся абстрактные понятия абсолютно упругого и абсолютно неупругого ударов. На этом уроке мы займемся изучением различных ударов.