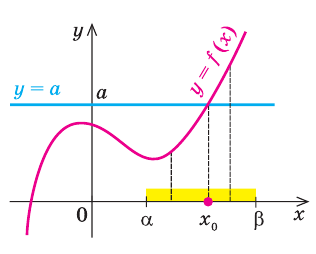
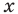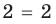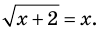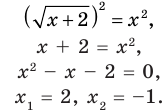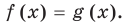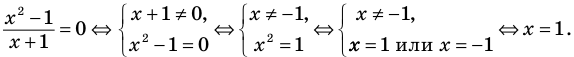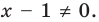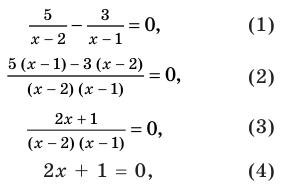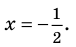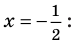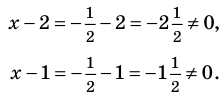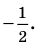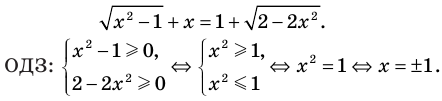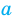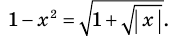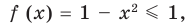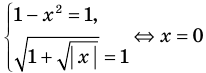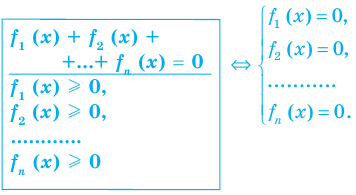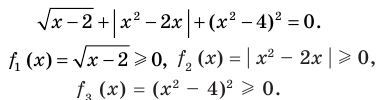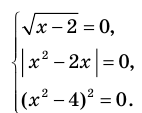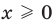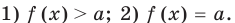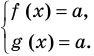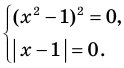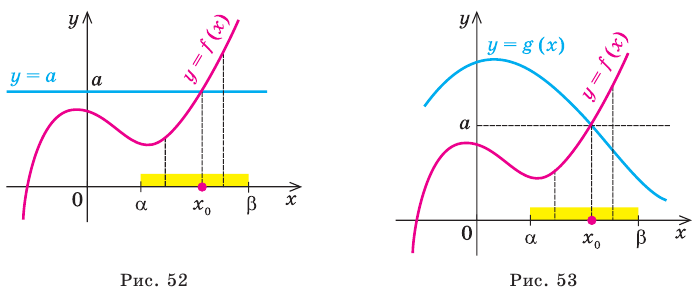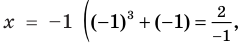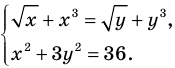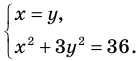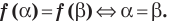- Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
- Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.
- Основные равносильные преобразования уравнений:
- Равносильные уравнения и уравнения следствия
- Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
- Уравнения и способы их решения
- Уравнение — определение и вычисление с примерами решения
- Уравнения
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- 📽️ Видео
Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
- Уравнения (x+2=7) и (2x+1=11) равносильны, так как каждое из них имеет единственный корень – число (5).
- Равносильны и уравнения (x^2+1=0) и (2x^2+3=1) — ни одно из них не имеет корней.
- А вот уравнения (x-6=0) и (x^2=36) неравносильны, поскольку первое имеет только один корень (6), второе имеет два корня: (6) и (-6).
Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Основные равносильные преобразования уравнений:
- Перенос слагаемых из одной части уравнения в другую со сменой знака слагаемого на противоположный.
Умножение или деление обеих частей уравнения на одно число или выражение не равное нулю.
Применение всех формул и свойств, которые есть в математике.
Возведение в нечетную степень обеих частей уравнения.
Извлечение корня нечетной степени из обеих частей уравнения.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Равносильные уравнения и уравнения следствия
Равносильные преобразования уравнений можно назвать «правильными» или «безошибочными» преобразованиями, потому что, сделав их, вы не нарушите математических законов. Почему тогда математики так их и не назвали: «правильные преобразования уравнений»? Потому что есть еще «полу-правильные» преобразования уравнений. В них уравнение при преобразовании приобретает дополнительные корни по ходу решения, но лишние корни мы при записи ответа не учитываем. Строгие математики их называют уравнениями следствиями:
Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
Пример (ОГЭ). Решите уравнение (x^2-2x+sqrt=sqrt+3)
Перенесем оба слагаемых из правой части в левую.
Взаимно уничтожим подобные слагаемые. Это и есть «полу-правильное преобразование», так как после него у уравнения становится два корня вместо изначального одного.
Это уравнение следствие из предыдущего. Найдем корни уравнения по теореме Виета .
Сверяем корни с ОДЗ и исключаем неподходящие.
(↑) не подходит под ОДЗ
Переходить к уравнению следствию не запрещено, но при работе с ними нужно быть осторожным и не забывать про ОДЗ .
Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.
Решение:
В пункте a) применялось равносильное преобразование 1.
В пункте b) перешли к уравнению следствию, так как (sqrt) «ушло», то ОДЗ расширилось;
В пункте с) тоже перешли к уравнению следствию, из-за того что умножили на знаменатель;
В пункте d) применялось равносильное преобразование: «Извлечения корня нечетной степени из обеих частей уравнения»;
В пункте e) умножили обе части уравнения на (2) т.е. равносильно преобразовали;
В пункте f) перешли от вида (a^=a^) к виду (f(x) =g(x)), что тоже является равносильным преобразованием.
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Уравнения и способы их решения
Министерство общего и профессионального образования РФ
Муниципальное образовательное учреждение
на тему: Уравнения и способы их решения
Выполнил: ученик 10 «А» класса
Проверила: учитель математики Исхакова Гульсум Акрамовна
3. Основная часть . 3
4. Заключение . 25
5. Приложение . 26
6. Список использованной литературы . 29
2. Историческая справка.
3. Уравнения. Алгебраически уравнения.
а) Основные определения.
б) Линейное уравненение и способ его решения.
в) Квадратные уравнения и способы его решения.
г) Двучленные уравнения способ их решения.
д) Кубические уравнения и способы его решения.
е) Биквадратное уравнение и способ его решения.
ё) Уравнения четвертой степени и способы его решения.
ж) Уравнения высоких степеней и способы из решения.
з) Рациональноное алгебраическое уравнение и способ его
и) Иррациональные уравнения и способы его решения.
к) Уравнения, содержащие неизвестное под знаком.
абсолютной величины и способ его решения.
4. Трансцендентные уравнения.
а) Показательные уравнения и способ их решения.
б) Логарифмические уравнения и способ их решения.
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. Я расположил материал по степени его сложности, начиная с самого простого. В него вошли как известные нам виды уравнений из школьного курс алгебры, так и дополнительный материал. При этом я попытался показать виды уравнений, которые не изучаются в школьном курсе, но знание которых может понадобиться при поступлении в высшее учебное заведение. В своей работе при решении уравнений я не стал ограничиваться только действительным решением, но и указал комплексное, так как считаю, что иначе уравнение просто недорешено. Ведь если в уравнении нет действительных корней, то это еще не значит, что оно не имеет решений. К сожалению, из-за нехватки времени я не смог изложить весь имеющийся у меня материал, но даже по тому материалу, который здесь изложен, может возникнуть множество вопросов. Я надеюсь, что моих знаний хватит для того, чтобы дать ответ на большинство вопросов. Итак, я приступаю к изложению материала.
Математика. выявляет порядок,
симметрию и определенность,
а это – важнейшие виды прекрасного.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37. «, — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
уравнения. Алгебраические уравнения
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв [1]). Для записи тождества наряду со знаком 

Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:













В общем виде уравнение может быть записано так:





В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество, называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения уравнения 






называют эквивалентными , если каждое из них является следствие другого, и пишут


Таким образом, два уравнения считаются эквивалентными, если множество решений этих уравнений совпадают.
Уравнение 





Н е к о т о р ы е э к в и в а л е н т н ы е у р а в н е н и я:
1) Уравнение 

2) Уравнение 

3) 


4) Уравнение 

5) Уравнение 




Алгебраическим уравнением называется уравнение вида

где 
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида




где n – неотрицательное целое число; коэффициенты многочлена 




Значения неизвестного х, обращающие алгебраическое уравнение в тождество, называются корнями (реже решениями ) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида F(х)
Так вот, главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка(и) пересечения двух графиков даст решение(я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Линейным уравнением называется уравнение первой степени.

где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень 
Прибавляя к обеим частям уравнения (1) число 

эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину 

Алгебраическое уравнение второй степени.

где 



Корни квадратного уравнения вычисляются по формуле

Выражение 
если 
если 
если 


Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если 

Корни приведенного квадратного уравнения вычисляются по формуле

Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде


Корни этого квадратного уравнения удобно вычислять по формуле

Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета


В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если 

если 

если 

если 

Перепишем еще раз квадратное уравнение

и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если



то корни квадратного уравнения вычисляются по формуле



которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).

Заметим, что 







но 

Если положить, что 


Заметим, что 


но 








Уравнения n-й степени вида

называется двучленным уравнением . При 


где 

которое и будет далее рассматриваться.
Двучленное уравнение 





Двучленное уравнение 

Двучленное уравнение 





Двучленное уравнение 

Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
1) 

Уравнение имеет два действительных корня 
2) 

Уравнение имеет один дествительный корень 

3) 

Уравнение имеет два действительных корния 

4) 

Уравнение действительных корней не имеет. Комплексные корни: 
5) 

Уравнение имеет один дествительный корень 

6) 

Уравнение действительных корней не имеет. Комплексные корни:


Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида


оказались «крепким орешком». В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида


разделить на 


Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь 


Мы видим, что надлежащим выбором 



Если здесь сделать замену 



Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида

Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:

Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу 


Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений

и взять в качестве 




Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при 



Выпишем эти корни:
Переменные 




Эта формула известная как формула Кардано .
подстановкой 



Корни 







Пусть «неполное» кубичное уравнение (14) действительно.
а) Если 




(b) Если 






(с) Если 







Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.

где a, b, c – некоторые действительные числа, называется биквадратным уравнением . Заменой 





Если 



Если 



Если 



Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари .
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
можно избавиться от члена 


Идея Феррари состояла в том, чтобы представить уравнение в виде 










Правая часть этого уравнения – квадратный трехчлен от 


Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно 



а само уравнение сводится к двум квадратным:

Их корни и дают все решения исходного уравнения.
Решим для примера уравнение

Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
и добавим к обеим частям выражение 

Теперь приравняем к нулю дискриминант правой части уравнения:

или, после упрощения,

Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: 

откуда 


подстановкой 

Корни 




в которых сочетания знаков выбираются так, чтобы удовлетворялось условие

причем 



Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени 

После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше ? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени 

Таким образом, общей формулы, применимой ко всем уравнениям данной степени 


с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его «Мемуаре об условиях разрешимости уравнений в радикалах» (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь 





Для доказательства достаточно подставить в уравнение 



Все слагаемые в левой части, кроме последнего, делятся на 







С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа «кандидатов». Например, для уравнения

старший коэффициент которого равен 1, «кандидатами» будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: 
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
остаток от деления многочлена 



Из теоремы непосредственно следует, что
Если 





Продолжая наш пример, вынесем из многочлена
множитель 



Но есть и более простой способ. Он станет понятен из примера:



Метод неопределенных коэффициентов
Если у многочлена с целыми коэффициентами рациональных корней не оказалось, можно попробовать разложить его на множители меньшей степени с целыми коэффициентами. Рассмотрим, например, уравнение

Представим левую часть в виде произведения двух квадратных трехчленов с неизвестными (неопределенными) коэффициентами:

Раскроем скобки в правой части и приведем подобные:

Теперь, приравнивая коэффициенты при одинаковых степенях 
Попытка решить эту систему в общем виде вернула бы нас назад, к решению исходного уравнения. Но целые корни, если они существуют, нетрудно найти и подбором. Не ограничивая общности, можно считать, что 




Если уравнение имеет вид 





Возвратным алгебраическим уравнением называется уравнение четной степени вида

в которых коэффициенты, одинаково отстоят от концов, равны: 



Рассмотрим, например, уравнение

Поделив его на 



Поэтому величина 

решив которое можно найти 

При решении возвратных уравнений более высоких степеней обычно используют тот факт, что выражение 



Рациональные алгебраические уравнения
Рациональным алгебраическим уравнением называется уравнение вида

где 



Множество допустимых значений рационального алгебраического уравнения (17)
задается условием 







Метод решения уравнения (17) заключается в следующем. Решаем уравнение

корни которого обозначим через

Сравниваем множества корней многочленов 









П р и м е р. Найдем действительные корни уравнения

где 

Многочлен 


Многочлен 


Решая то же самое уравнение в множестве комплексных чисел, получим, что уравнение 


Уравнение, содержащее неизвестное (либо рациональное алгебраическое выражение от неизвестного) под знаком радикала, называют иррациональным уравнением . В элементарной математике решения иррациональных уравнений отыскивается в множестве действительных чисел.
Всякое иррациональное уравнение с помощью элементарных алгебраических операций (умножение, деление, возведение в целую степень обеих частей уравнения) может быть сведено к рациональному алгебраическому уравнению. При этом следует иметь в виду, что полученное рациональное алгебраическое уравнение может оказаться неэквивалентным исходному иррациональному уравнению, а именно может содержать «лишние» корни, которые не будут корнями исходного иррационального уравнения. Поэтому, найдя корни полученного рационального алгебраического уравнения, необходимо проверить, а будут ли все корни рационального уравнения корнями иррационального уравнения.
В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного иррационального уравнения получилось не просто какое-то рациональное алгебраическое уравнение, среди корней которого будут и корни данного иррационального уравнения, а рациональное алгебраическое уравнение образованное из многочленов как можно меньшей степени. Желание получить то рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени, вполне естественно, так как нахождение всех корней рационального алгебраического уравнения само по себе может оказаться довольно трудной задачей, решить которую полностью мы можем лишь в весьма ограниченном числе случаев.
Приведем некоторые стандартные, наиболее часто применяемые методы решения иррациональных алгебраических уравнений.
1) Одним из самых простых приемов решения иррациональных уравнений является метод освобождения от радикалов путем последовательного возведения обеих частей уравнения в соответствующую натуральную степень. При этом следует иметь в виду, что при возведении обеих частей уравнения в нечетную степень полученное уравнение, эквивалентное исходному, а при возведении обеих частей уравнения в четную степень полученное уравнение будет, вообще говоря, неэквивалентным исходному уравнению. В этом легко убедиться, возведя обе части уравнения
в любую четную степень. В результате этой операции получается уравнение
множество решений которого представляет собой объединение множеств решений:


Однако, несмотря на этот недостаток, именно процедура возведения обеих частей уравнения в некоторую (часто четную) степень является самой распространенной процедурой сведения иррационального уравнения к рациональному уравнению.
П р и м е р 1. Решить уравнение

где 


В силу определения операции извлечения корня в множестве действительных чисел допустимые значения неизвестного 


Возведя обе части уравнения (18) в квадрат, получим уравнение

После повторного возведения в квадрат уравнение превращается в алгебраическое уравнение

Так как обе части уравнения (18) возводились в квадрат, может оказаться, что не все корни уравнения (19) будет являться решениями исходного уравнения, необходима проверка корней.
2) Другим примером решения иррациональных уравнений является способ введения новых неизвестных, относительно которых получается либо более простое иррациональное уравнение, либо рациональное уравнение.
П р и м е р 2. Решить иррациональное уравнение

Множество допустимых значений этого уравнения:

Положив 
или эквивалентное ему уравнение

которое можно рассматривать как квадратное уравнение относительно 


Следовательно, множество решений исходного иррационального уравнения представляет собой объединение множеств решений следующих двух уравнений:


Возведя обе части каждого из этих уравнений в куб, получим два рациональных алгебраических уравнения:


Решая эти уравнения, находим, что данное иррациональное уравнение имеет единственный корень 
В заключение заметим, что при решении иррациональных уравнений не следует начинать решение уравнение с возведения обеих частей уравнений в натуральную степень, пытаясь свести решение иррационального уравнения к решению рационального алгебраического уравнения. Сначала необходимо посмотреть, нельзя ли сделать какое-нибудь тождественное преобразование уравнения, которое может существенно упростить его решение.
П р и м е р 3. Решить уравнение

Множество допустимых значений данного уравнения: 

Далее, записывая уравнение в виде

при 
при 

При 

При 

Принимая во внимание, что множество допустимых решений уравнения определяется условием 
При 

При всех остальных значениях 
Уравнения, содержащие неизвестное под знаком абсолютной величины
Уравнения, содержащие неизвестное под знаком абсолютной величины, можно свести к уравнениям, не содержащим знака абсолютной величины, используя определение модуля. Так, например, решение уравнения

сводится к решению двух уравнений с дополнительными условиями.
1) Если 

Решения этого уравнения: 


2) Если 

Корнями этого уравнения будут числа 



Таким образом, решениями уравнения (21) будут числа 3 и 
Заметим, что коэффициенты уравнения, содержащего неизвестное под знаком абсолютной величины, можно подобрать таким образом, что решениями уравнения будут все значения неизвестного, принадлежащие некоторому промежутку числовой оси. Например, решим уравнение

Рассмотрим числовую ось Ох и отметим на ней точки 0 и 3 (ноли функций, стоящих под знаком абсолютной величины). Эти точки разобьют числовую ось на три промежутка (рис. 1):



 |
1) При 

В промежутке 
Аналогично, при 
и в промежутке 
2) При 

т. е. обращается в тождество. Следовательно, любое значение 
Уравнение, не сводящееся к алгебраическому уравнению с помощью алгебраических преобразований, называется трансцендентным уравнением [4]).
Простешими трансцендентными уравнениями являются показательные, логарифмические и тригонометрические уравнения.
Показательным уравнением называется уравнение, в котором неизвестное входит только в показатели степеней при некоторых постоянных основаниях.
Простейшим показательным уравнением, решение которого сводится к решению алгебраического уравнения, является уравнение вида

где 



В простейшем случае, когда 
Множество решений показательного уравнения вида

где 
Вводится новая переменная 

П р и м е р 1. Решить уравнение

Записывая уравнение в виде
и вводя новую переменную 


Нетрудно убедиться, что данное кубическое уравнение имеет единственный рациональный корень 


Таким образом, решение исходного уравнения сведено к решению простейших показательных уравнений:



Последнее из перечисленных, уравнений решений не имеет. Множество решений первого и второго уравнений:


Н е к о т о р ы е п р о с т е й ш и е п о к а з а т е л ь н ы е у р а в н е н и я:
1) Уравнение вида
заменой 

2) Уравнение вида
заменой 

3) Уравнение вида
заменой 

Логарифмическим уравнением называется уравнение, в котором неизвестное входит в виде аргумента логарифмической функции.
Простейшим логарифмическим уравнением является уравнение вида

где 


В простейшем случае, когда 

Множество решений логарифмического уравнения вида 

Вводится новая переменная 

П р и м е р 1. Решить уравнение

Относительно неизвестного 

Корни этого уравнения: 

Решая логарифмические уравнения


получаем решения логарифмического уравнения (27): 

В некоторых случаях, для того чтобы свести решение логарифмического уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо предварительно сделать подходящие преобразования логарифмов, входящих в уравнение. Такими преобразованиями могут быть преобразование суммы логарифмов двух величин в логарифм произведения этих величин, переход от логарифма с одним основанием к логарифму с другим основанием и т. д.
П р и м е р 2. Решить уравнение

Для того чтобы свести решение данного уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо прежде всего привести все логарифмы к одному основанию (здесь, например, к основанию 2). Для этого воспользуемся формулой

в силу которой 



Заменой 


Корни этого квадратного уравнения: 





П р и м е р 3. Решить уравнение

Преобразуя разность логарифмов двух величин в логарифм частного этих величин:

сводим данное уравнение к простейшему логарифмическому уравнению

Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
В данной работе были представлены далеко не все, способы решения уравнений и даже не все их виды, а только самые основные. Я надеюсь, что мое сочинение может послужить неплохим справочным материалом при решении тех или иных уравнений. В заключении хотелось бы отметить, что при написании данного сочинения я не ставил себе цели показать все виды уравнений, а излагал лишь имеющийся у меня материал.
Список использованной литературы
1. Глав. ред. М. Д. Аксенова. Энциклопедия для детей. Том 11. Математика. – М.: Аванта+, 1998. – 688 с.
2. Цыпкин А. Г. Под ред. С. А. Степанова. Справочник по математике для средней школы. – М.: Наука, 1980.- 400 с.
3. Г. Корн и Т. Корн. Справаочник по математике для начуных работников и инженеров. – М.: Наука, 1970.- 720 с.
[1]) Под допустимыми понимаются те численные значения букв, при которых выполнимы все операции, совершаемые над буквами, входящими в равенство. Например, допустимыми значениями букв, входящих в равенство
будут следующие; для 

[2]) Если a и b имеют разные знаки, то 
[3]) Случай 

[4]) Под алгебраическими преобразованиями уравнения
Понимают следующие преобразования:
1) прибавление к обеим частям уравнения одного и того же алгебраического выражения;
2) умножение обеих частей уравнения на одно и то же алгебраическое выражение;
3) возведение обеих частей уравнения в рациональную степень.
Видео:Корень n-ой степени. Алгебра, 9 классСкачать

Уравнение — определение и вычисление с примерами решения
Содержание:
Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
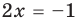
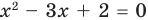
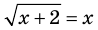
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
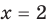
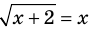
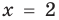
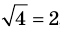
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 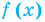
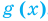
Для уравнения 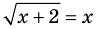
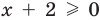
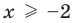
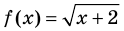

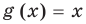
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 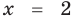
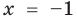
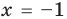
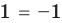
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
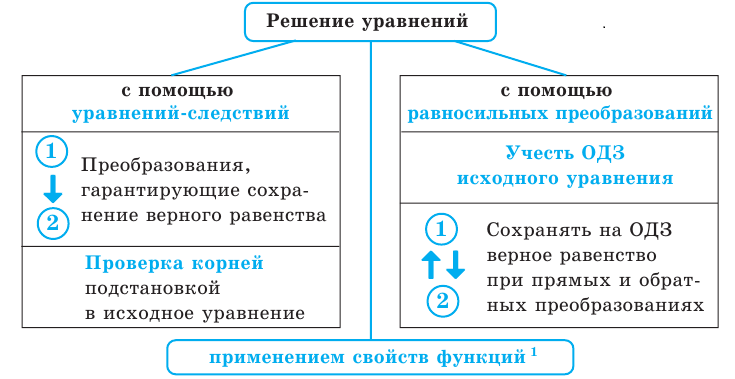
5. Схема поиска плана решения уравнений



Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 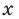
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 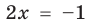
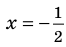
а уравнение 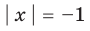
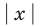
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 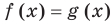
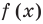
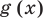
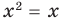
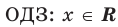
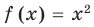
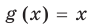
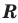
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 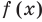
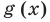
Например, в уравнении 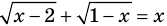
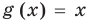
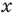
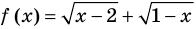
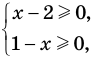
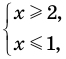
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 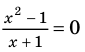
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 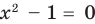
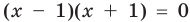
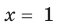
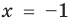
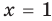
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
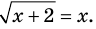
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
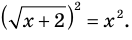
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 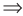
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 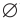
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 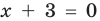
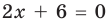
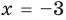
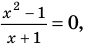
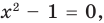
то, как было показано выше, уравнение (3) имеет единственный корень 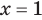
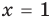
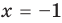
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 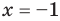
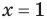
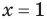
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 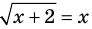
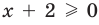

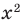
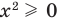
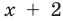


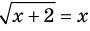
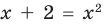
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 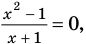
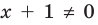
Запись решения в этом случае может быть такой:
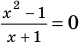
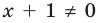
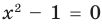
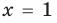
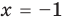
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 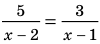
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 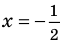
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
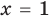
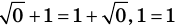
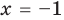
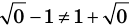
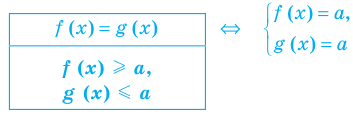
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 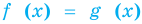


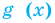
Пример:
►
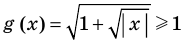
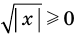
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 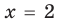
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 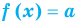
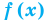
Пример:
Уравнение 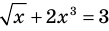
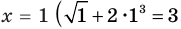
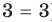
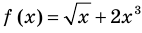
Если в уравнении 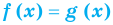
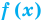
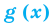
Пример:
Уравнение 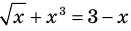
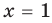
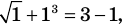
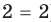
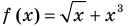

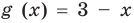
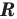
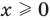
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 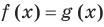
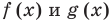
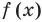
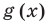
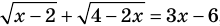
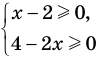
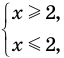


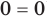


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 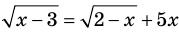
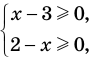
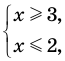
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 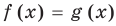
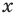
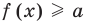
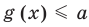
Рассмотрим два случая:
Если 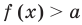
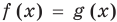
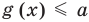
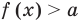
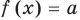
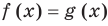
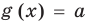
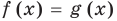
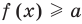
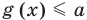
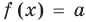
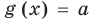
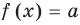
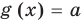
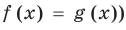
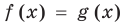
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 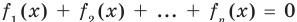
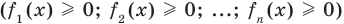
Если предположить, что 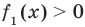

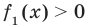
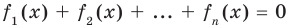
Например, чтобы решить уравнение 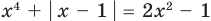
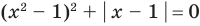
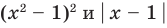
Из второго уравнения получаем 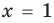
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 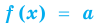
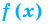
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 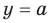
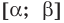
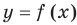
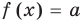
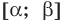
• Если на промежутке 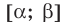
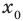
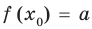
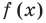
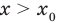
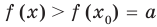
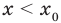
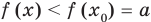
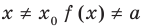
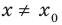
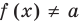
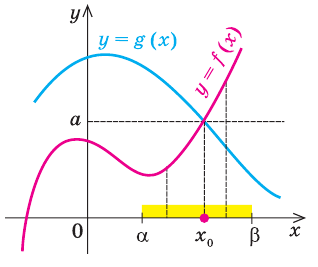
Теорема 2. Если в уравнении 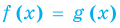
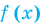
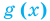
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 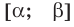
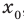
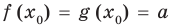
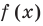
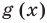
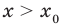
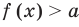
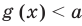
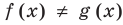
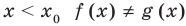
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 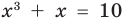
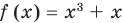

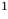
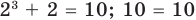
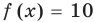
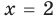
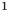

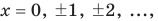
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 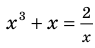
► Сначала следует учесть его ОДЗ: 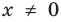
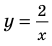
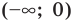
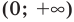
1) При 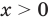
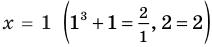
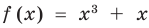

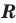
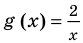

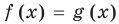
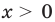
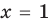
2) При 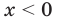
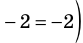
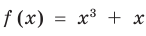
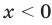
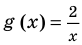
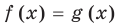
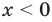
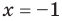
Примеры решения задач:
Пример №424
Решите уравнение 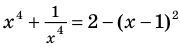
Решение:
► ОДЗ: 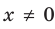
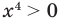
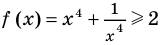
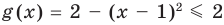
Таким образом, данное уравнение равносильно системе 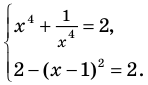


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 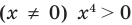
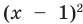
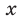
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 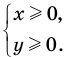
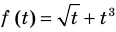
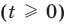
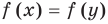
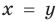
Подставляя 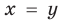
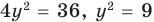
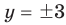

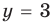
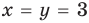
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 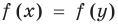
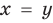
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 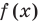
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📽️ Видео
Корень n-ой степени из действительного числа и его свойства. 11 класс.Скачать

Вариант 39, № 2. Линейное уравнение, имеющее бесконечно много корнейСкачать

Имеет ли уравнение действительные корни?Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Быстрый способ решения квадратного уравненияСкачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Комплексные корни квадратного уравненияСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать