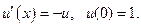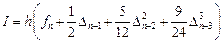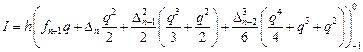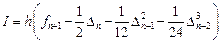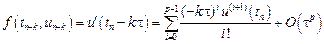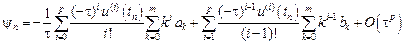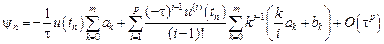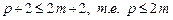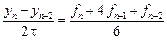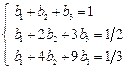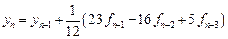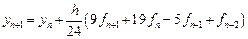Если в один и тот же момент времени выполняются одновременно несколько операций обработки данных, то такие вычисления называются параллельными[1]. Потребность решения сложных прикладных задач с большим объемом вычислений и принципиальная ограниченность максимального быстродействия «классических» — по схеме фон Неймана — ЭВМ привели к появлению многопроцессорных вычислительных систем. Использование таких средств вычислительной техники позволяет существенно увеличивать производительность ЭВМ при любом существующем уровне развития компьютерного оборудования. При этом, однако, необходимо «параллельное» обобщение традиционной — последовательной — технологии решения задач на ЭВМ. Так, численные методы в случае многопроцессорных вычислительных систем должны проектироваться как системы параллельных и взаимодействующих между собой процессов, допускающих исполнение на независимых процессорах. Применяемые алгоритмические языки и системное программное обеспечение должны обеспечивать создание параллельных программ, организовывать синхронизацию и взаимоисключение асинхронных процессов.
Проблема создания высокопроизводительных вычислительных систем является одной из наиболее сложных научно-технических задач современности и ее решение возможно только при концентрации усилий многих талантливых ученых и конструкторов, предполагает использование всех последних достижений науки и техники и требует значительных финансовых инвестиций.
- 1. Типовые структуры линий связи параллельных ВС
- 2. Численные методы решения задач Коши для ОДУ
- 3. Многошаговые методы решения задач Коши для ОДУ
- 3.1 Явные многошаговые методы Адамса-Башфорта
- 3. 2 Неявные многошаговые методы Адамса-Мултона
- 4 Параллельные методы численного решения задачи Коши для ОДУ
- 5 Оценка параллелизма многошаговых блочных методов
- Выводы
- Общая формулировка многошаговых методов
- 🎬 Видео
1. Типовые структуры линий связи параллельных ВС
Топология ВС – это способ соединения компьютеров в единую ВС.
К числу типовых топологий относят[2]:
— Линейка ( linear array or farm ) – представляет собой линейный массив процессоров (рис.1).
Рисунок 1 – Сеть процессоров с топологией линейка
Система, в которой каждый процессор имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами; такая схема является, с одной стороны, просто реализуемой, а с другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений);
— Кольцо ( ring ) – данная топология аналогична топологии линейка с тем учетом, что первый и последний компьютер соединены (рисунок 2). Связи в могут быть однонаправленными или двунаправленными. [6] Кольцевая структура сохраняет достоинства, а также сокращает максимальное расстояние между процессорами – n /2 [5].
Рисунок 2 – Сеть с топологией кольцо
— Решетка (2D-решетка, матрица, сетка – mesh) – система, в которой граф линий связи образует прямоугольную сетку, то есть процессоры расположены в виде правильной двумерной решетки и каждый процессор (кроме крайних) соединен с четырьмя соседями (рисунок 3)
Рисунок 3 – Сеть с топологией решетка
Достоинством такой схемы является простота, а недостаток состоит в том, что при обмене между отдаленными процессорами данные должны пройти через ряд промежуточных процессоров.
— Гиперкуб ( hypercube ) – данная топология представляет частный случай решетки, когда по каждой размерности сетки имеется только два процессора (то есть гиперкуб содержит n = 2 N процессоров при размерности N ).
Рисунок 4 – Сеть с топологией 3-х мерный гиперкуб
Также может быть схема соединения процессоров в четырехмерном кубе. Эта схема приведена на рисунке 5.
Рисунок 5 – Сеть с топологией 4-х мерный гиперкуб
Топология гиперкуб предоставляет возможность моделировать некоторые важные типы связей: линейка, кольцо, решетка.
— Клика или полный граф ( completely — connected graph or clique ) – система, в которой связи процессоров образуют полный граф.
Рисунок 6 – Сеть с топологией клика
— Звезда ( star ) – система, в которой все процессоры имеют линии связи с некоторыми управляющим процессором (рисунок 7). Данная топология является эффективной при организации централизованных схем параллельных вычислений.
Рисунок 7 – Сеть с топологией звезда
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

— «Толстое дерево» («fat-tree», hypertree) – архитектура процессоры в которой локализованы в листьях дерева, в то время как внутренние узлы дерева скомпонованы во внутреннюю сеть. Поддеревья могут общаться между собой, не затрагивая более высоких уровней сети. (рисунок 8, 9)
Рисунок 8 – Сеть с архитектурой «Fat-tree»
Рисунок 8 – Сеть с архитектурой «Fat-tree» (вид сверху)
При этом данная топология является наиболее эффективной.
Реальные высокопроизводительные параллельные вычислительные системы обычно используют несколько различных схем соединения процессоров. Это позволяет сочетать лучшие качества известных топологий и минимизировать недостатки. А также, поскольку способ соединения процессоров друг с другом больше влияет на производительность кластера , чем тип используемых в ней процессоров, то может оказаться более целесообразным создать систему из большего числа дешевых компьютеров, чем из меньшего числа дорогих[8].
Решение различных прикладных задач требует решения обыкновенных дифференциальных уравнений или систем обыкновенных дифференциальных уравнений высокого порядка. Сокращение времени решения, а, следовательно, и времени моделирования, возможно при использовании параллельных вычислительных систем, эффективность работы которых существенно зависит от характеристик применяемых параллельных алгоритмов.
2. Численные методы решения задач Коши для ОДУ
Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение вида [3] (в него входят: независимая переменная t, неизвестная x и ее производные по t )
где, как правило, обозначается значения неизвестной функции буквой x, независимой переменной — t (и интерпретировать ее как время), производных от x по t — x’, x», . x(m). Также используется сокращенное обозначение J(m)x = (x, x’, . x(m)) — этот вектор называют струей, или джетом m-го порядка функции x в точке t. В дифференциальные уравнения может входить также набор C = (C1, C2, . Cp) произвольных постоянных (параметров) [9].
В свою очередь, порядком ОДУ называется порядок старшей производной искомой функции.
Общим интегралом уравнения называют функцию 
т.е. решение x(t) входитнеявным образом, причем количество констант интегрирования равно порядку ОДУ
Общим решением ОДУ называется функция
связывающая независимую переменную t и n констант интегрирования C i , т.е. решение x(t) определяется явным образом.
Для определения констант интегрирования С i задаются дополнительные условия в количестве, равном количеству констант интегрирования или порядку ОДУ.
Если в дополнительные условия подставить исходное уравнение и решить полученную систему относительно С i , а затем подставить в общий интеграл, то получим частное решение или частный интеграл

Аналогичные процедуры с общим решением (3) дают частный интеграл
Если все дополнительные условия задаются в одной точке x 0 , то совокупность ОДУ и дополнительных условий называют задачей Коши для рассматриваемого ОДУ. В этом случае дополнительные условия называют начальными условиями.
Если дополнительные условия задаются более чем в одной точке, то совокупность ОДУ и дополнительных условий называют краевой задачей Коши для рассматриваемого ОДУ, а дополнительные условия называют граничными или краевыми условиями.
3. Многошаговые методы решения задач Коши для ОДУ
Методы решения ОДУ бывают одношаговые и многошаговые. К одношаговым относятся: метод Эйлера, метод Рунге – Кутты и др., а к многошаговым: линейные многошаговые разностные методы, в том числе методы Адамса-Башфорта и методы Адамса-Мултона.
В многошаговых методах повышение точность вычисления происходит за счет использования информации о поведении решения на предыдущих шагах.
Общая схема построения m-шаговых разностных методов, используемых для приближенного решения задачи Коши [4]

выглядит следующим образом

где 



Наиболее простые и наиболее часто встречающиеся вычислительные правила для многошаговых методов имеют вид:

Среди правил (5) особенно широко известны явные (экстраполяционные) при 

3.1 Явные многошаговые методы Адамса-Башфорта
Все m –шаговые методы Адамса, полученные из формулы (3), положив в ней 

Определить коэффициенты формулы (4) можно следующим образом. Пусть известно приближенное решение 









Проводя интегрирование, получим разностную схему для решения дифференциального уравнения. Порядок схемы определяется величиной остаточного члена интерполяционного полинома. По существу, интерполяционный многочлен 



Рассмотрим случай при m =2. В этом случае соответствующий многочлен Ньютона будет иметь вид:
Видео:Решение обыкновенных дифференциальных уравнений. Часть 1Скачать

Подставив его в формулу (7) мы получим:
А после интегрирования формула для вычисления приближенного решения будет иметь вид:
3. 2 Неявные многошаговые методы Адамса-Мултона
Неявные m-шаговые методы Адамса определяются формулой (6) при 

Построение интерполяционных m- шаговых методов Адамса-Мултона может быть осуществлено совершенно аналогично случаю экстраполяционных формул. Для этого следует использовать интеграл (5) , в котором интерполяционный многочлен 

Приведем интерполяционные формулы Адамса различных порядков точности:
двухшаговый неявный разностный метод Адамса- Мултона

трехшаговый неявный разностный метод Адамса – Мултона

Определение порядка аппроксимации неявных методов Адамса-Мултона выполняется аналогично определению невязки методов Адамса-Башфорта
Погрешность аппроксимации трех шагового метода Адамса – Мултона равна
Заметим, что во всех приведенных выше интерполяционных формулах Адамса значение 



действительно является уравнением относительно неизвестного значения 
На практике обычно не решают уравнение (9), а используют совместно явную и неявную формулы (метод Адамса-Бошфорта-Мултона), что приводит к методу прогноза и коррекции. Одним из широко используемых методов прогноза и коррекции является объединение методов Адамса четвертого порядка точности

При такой последовательности вычислений этот метод является явным
4 Параллельные методы численного решения задачи Коши для ОДУ
В данной главе будут рассмотрены основы распараллеливания одношаговых и многошаговых алгоритмов методов решения задачи Коши для ОДУ [5].
Для простоты понимания и вывода формул, будем рассматривать решение задачи Коши для одного обыкновенного дифференциального уравнения первого порядка
Множество M точек равномерной сетки , m = 

В общем случае уравнения многошаговых разностных методов для блока из k точек при использовании вычисленных значений приближенного решения в m предшествующих блоку узлах, с учетом введенных выше обозначений можно записать в виде:


5 Оценка параллелизма многошаговых блочных методов
Для оценки ускорения m -шагового k -точечного блочного метода сравним время его выполнения на мультипроцессорной системе со временем выполнения алгоритма m -шагового метода Адамса-Башфорта на однопроцессорной ЭВМ. [5] Метод Адамса-Башфорта можно рассматривать как многошаговый одноточечный блочный метод. Последовательное k -кратное применение формул Адамса-Башфорта позволяет вычислить приближенное решение в тех же k узлах блока, в которых параллельно за k итераций может быть вычислено решение m -шаговым k -точечным блочным методом. В этом случае время вычисления будет приблизительно одинаково. Точность приближенного решения, полученного m -шаговым k -точечным блочным методом, имеет порядок O( 

Здесь 



ЭВМ и сравним времена решения задачи m -шаговым k -точечным блочным методом на однопроцессорной линейке k процессоров . Закрепим за каждым узлом блока процессор. Используя обозначения, введенные в п. 7.3. получим для времени вычисления на одном процессоре с локальной точностью O( 
Время параллельного вычисления приближенных значений решения на линейке из процессоров с той же точностью для всех узлов блока составит
Ускорение параллельных многоточечных алгоритмов можно вычислиь по формуле
Если учитывать только время вычислений правой части уравнений, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части, то ускорение k точечного многошагового параллельного алгоритма можно считать приближенно равным
и эффективность будет равна
Отсюда следует, что при решении на однопроцессорной ЭВМ решение m -шаговым k -точечным блочным методом потребует меньше времени, чем решение этой же задачи соответствующим методом Адамса — Башфорта.
Выводы
В данный момент все чаще и чаще приходится касаться вопросов вычислительной мощности систем. Одним из способов повышения этой мощности является организация параллельных систем.
В данной работе рассмотрены параллельные алгоритмы решения задачи Коши, как многошаговых, так и одношаговых. Повышение производительности параллельных алгоритмов происходит за счет одновременного вычисления нескольких значений. В свою очередь повышение точности вычислений многошаговых методов происходит за счет учета найденных решений в нахождении новых. Т.о. параллельные многошаговые методы обладают высокой производительностью и высокой точностью вычислений.
Общая формулировка многошаговых методов
Многошаговые методы
Решения задачи коши
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
Видео:7.4 Многошаговые методыСкачать

9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение yn+1 определяется лишь значениями tn, yn и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках yn-1, yn-2,
Многошаговые методы строятся на равномерной сетке
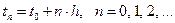
Обозначим: 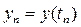
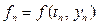
Линейный m-шаговый метод можно описать формулой:

Многошаговые методы не являются самостартующими. Для использования m-шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения 
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 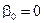
Если 
Частным случаем многошаговых методов являются методы Адамса:
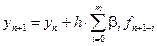
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 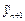

Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:

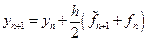
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
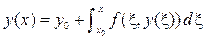
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки xn можно записать следующим образом

В формуле (9.4) 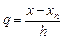

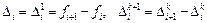

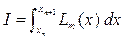
Найдем вначале формулы для двухшагового метода m=2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции 

и 
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:

При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки xn+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 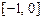
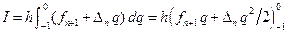
Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
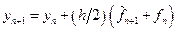
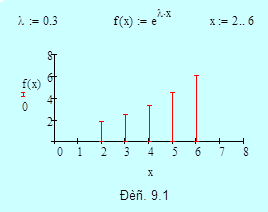
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
Точное решение представляет собой экспоненту 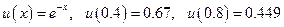
Выберем шаг приращения 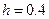
Начальное условие: 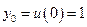
Дополнительное условие: 
С помощью формул (9.8) и (9.10) вычислим значение 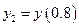
По формуле предиктор получаем: 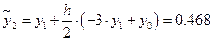
По формуле корректор уточняем решение: 
Для сравнения приведем расчеты значения 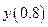

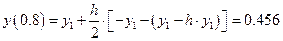
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
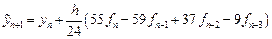
Вывод формулы корректор.
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
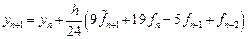
Общая формулировка многошаговых методов
Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Для решения задачи Коши
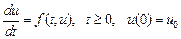
введем сетку с постоянным шагом 

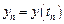

Линейным m-шаговым разностным методом называется система разностных уравнений
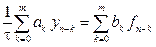
где 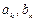
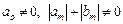
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 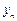
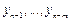
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки

Метод называется явным, если 
Если 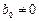
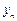

Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв 
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
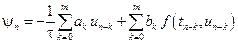
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).
Подставим эти разложения в формулу для невязки
Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
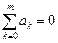
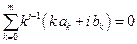

Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов ak, bk. К этим уравнениям нужно добавить еще условие нормировки (9.15): 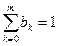
Для неявного метода имеем 2m+2 неизвестных: 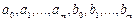
– для неявного метода порядок аппроксимации не превышает 2m.
Для явного метода имеем 2m+1 неизвестных: 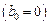
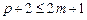
Преобразуем систему уравнений для коэффициентов ak, bk. С учетом условия нормировки уравнение 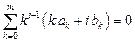
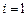
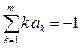
Окончательно получаем систему уравнений для коэффициентов линейного m-шагового разностного метода общего вида:
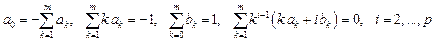
На практике часто используются методы Адамса, которые описываются формулой
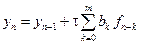
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты bk.

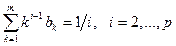
Имеем p уравнений. В случае неявного метода Адамса имеется m+1 неизвестных: 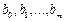
Рассмотрим варианты двухшаговых методов m=2. Максимальный порядок двухшагового метода равен p=4, так что можно написать следующую систему уравнений.
Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 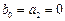
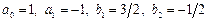

2) Положив 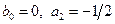

3) Положив 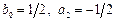
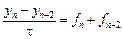
Варианты методов третьего порядка.
1) Положив 
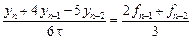
2) Если выбрать 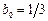

3) Выбрав 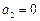
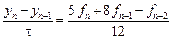
Метод четвертого порядка получим, используя все шесть уравнений:
Явный трехшаговый метод имеет порядок p=3. В соответствии с формулами (9.20) для нахождения коэффициентов bk имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i: 
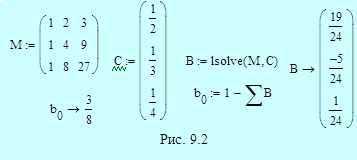
Неявный метод имеет четвертый порядок, и для коэффициентов 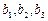
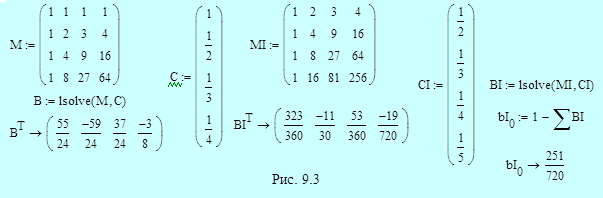 |
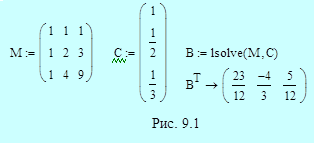
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
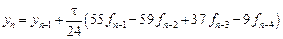
- неявный метод пятого порядка
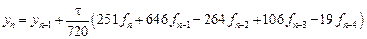
🎬 Видео
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

3_05. Многошаговые алгоритмы решения ОДУСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Численное решение задачи Коши методом ЭйлераСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Дифференциальные уравнения. 11 класс.Скачать

Метод ЭйлераСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

5 Численное решение дифференциальных уравнений Part 1Скачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать