Многочлены от нескольких переменных решение уравнений

Видео:11 класс, 2 урок, Многочлены от нескольких переменныхСкачать

Как решать многочлены от нескольких переменных — пояснения

Видео:Алгебра 10 класс (Урок№13 - Многочлены от нескольких переменных.)Скачать

Понятие многочлена от нескольких переменных

Одночлен — тип числа, переменные, их произведения и степени.

Многочлен — сумма различных одночленов. Примером многочлена может считаться уравнение 31 x y 5 + y 6 + 3 x z 5 .

Члены многочлена — абсолютно все одночлены, которые входят в состав многочлена.

Многочлен стандартного вида — тип многочлена, который состоит из одночленов стандартного вида, не имеющих соответствующих членов.

Степень многочлена стандартного вида — самая большая степень из перечня степеней одночленов, которые входят в его состав.

Для термина «многочлен нескольких переменных» возможно выделить несколько частных вариантов: трехчлен и двучлен.

Двучлен — такой многочлен, который состоит из двух членов. Примером двучлена служит следующее уравнение: 6 b 6 + 13 a c 5 .

Трехчлен — такой многочлен, который состоит из трех членов. Примером трехчлена служит следующее уравнение: x y 5 + y 6 + x z 5 .

При помощи многочлена вводят такие термины как «алгебраическое уравнение», «алгебраическое число», а также алгебраическая функция».

Виды многочленов

Существуют следующие виды многочленов:

• унитарным, приведенным, нормированным называют многочлен с одной переменной, если старший коэффициент равняется единице;
• однородным называют многочлен, при котором все одночлены обладают одной и той же полной степенью. Пример: x 2 + x y + y 2 является однородным многочленом с двумя переменными, а x 2 + y + 1 не будет считаться однородным;
• приводимым называется многочлен, который возможно разложить в виде произведения многочленов низших степеней с коэффициентами из определенного поля, а ином случае такой многочлен является неприводимым.

Многочлены от двух переменных

Для обозначения переменных возьмем две латинские буквы — y и x, которые обычно используются в алгебре. Представим произведение a × x k × y l , где a будет являться числом, которое можно назвать одночленом. Степень данного числа будет равна k+l. Сумма одночленов считается многочленом.

В отличие от многочленов с одной переменной, для многочленов, у которых большое количество переменных, не существует общепринятой шаблонной записи.

Как и многочлены с одной переменной, многочлены с несколькими переменными имеют способность к разложению на множители. Самым главным разложением является разложение разности n-ых степеней, которое более известно всем в использовании для n=2 и n=3.

x 2 — y 2 = ( x — y ) ( x + y )

x 3 — y 3 = ( x — y ) ( x 2 + x × y + y 2 )

Данные формулы можно обобщить для произвольного n:

x n — y n = ( x — y ) ( x n — 1 + x n — 2 × y + . . . + x × y n — 2 + y n — 1 )

Сумму n — ы х степеней возможно с легкостью разложить в тех случаях, когда n является нечетным. Слагаемое y n возможно представить в форме — ( — y ) n , а также применить формулу разложения разности n — ы х степеней.

x 5 + y 5 = x 5 — ( — y ) 5 = ( x — ( — y ) ) × ( x 4 + x 3 × ( — y ) + x 2 × ( — y ) 2 + x × ( — y ) 3 + ( — y ) 4 ) = ( x + y ) × ( x 4 — x 3 × y + x 2 × y 3 + y 4 ) .

Данное тождество может быть проверено прямым перемножением скобок правой части.

Многочлены от нескольких переменных

Как и в случае с двумя переменными возможно построить многочлены от любого количества переменных. Возьмем m количество букв x 1 , x 2 , … Совершим построение одночленов x k 1 , x l 2 , . . . , x z n . Многочленом называется сумма данных одночленов, которые снабжены числовыми коэффициентами.

Покажем ряд тождеств, в которых могут использоваться многочлены с несколькими переменными.

1 ) x 3 + y 3 + z 3 — 3 × x y z = ( x + y + z ) × ( x 2 + y 2 + z 2 — x y — y z — x z ,

2 ) ( a 2 + b 2 + c 2 ) × ( x 2 + y 2 + z 2 ) = ( z x + b y + c z ) 2 + ( a y — b x ) 2 + ( a z — c x ) 2 + ( b z — c y ) 2 ,

3 ) ( x — x 1 ) × ( x — x 2 ) × ( x — x 3 ) = x 3 — ( x 1 + x 2 + x 3 ) × x 2 + ( x 1 x 2 + x 2 x 3 + x 3 x 1 ) × x — x 1 x 2 x 3 .

Степень одночлена — такая сумма степеней, с которыми в данный одночлен входят все буквы. Степень многочлена — самая большая степень одночлена, входящего в многочлен (с условием ненулевого коэффициента). Рассмотрим примеры, которые приведены выше.

В первом примере в левой части находится многочлен третьей степени с разными переменными (обозначается буквами x, z, y).

Во втором примере многочлен находится в четвертой степени с переменными, которые обозначаются буквами a, b, c, x, y, z.

В третьем случае многочлен находится в третьей степени с четырьмя буквами x, x1, x2, x3.

Многочлен считается однородным в том случае, если все его одночлены обладают одним и тем же коэффициентом степени. В примерах выше все многочлены считаются однородными. Среди многочленов с несколькими буквами выделяют симметричные многочлены. В примерах выше первые два примера считаются симметричными. Можно особо отметить базовые симметричные многочлены, как и в варианте с двумя переменными.

F 0 = 1 , F 1 = x 1 + . . . + x m , F 2 = x 1 x 2 + . . . + x m — 1 x m , F m = x 1 x 2 × . . . × x m .

В данных формулах F n является суммой всех возможных произведений, которые взяты по k букв из информации m букв. Как и в случае с двумя буквами, каждый симметричный многочлен будет представлен в качестве многочлена от базовых симметричных многочленов.

Бином Ньютона является одним из самых известных многочленов от двух переменных. Бином представляет собой разложение степени двучлена ( a x + b y ) n в сумму одночленов.

Рассмотрим, какие действия можно совершать с многочленами.

Сумма многочленов

У многочленов существует способность складываться друг с другом. Приведем пару простых примеров.

Совершим сложение следующих уравнений:

3 x y 5 + 6 y 6 + 13 x 5 , а также 6 y 6 — x y 5 + 3 x 5 .

Первый этап сложения — записать данные многочлены в виде суммы:

( 3 x y 5 + 6 y 6 + 13 x 5 ) + ( 6 y 6 — x y 5 + 3 x 5 ) .

Далее нужно раскрыть скобки в данном уравнении:

3 x y 5 + 6 y 6 + 13 x 5 + 6 y 6 — x y 5 + 3 x 5 .

Далее нужно привести подобные слагаемые. В итоге получим следующее уравнение:

2 x y 5 + 12 y 6 + 16 x 5 .

Получается, что результат суммы данных двух многочленов дает такой же многочлен.

Разность многочленов

Также над данными типами чисел можно совершать действие вычитания. Рассмотрим небольшой пример данного действия.

Совершаем вычитание следующих уравнений:

3 x y 5 + 6 y 6 + 13 x 5 и 6 y 6 — x y 5 + 3 x 5 .

Первый шаг в решении такого типа заданий — записать данное уравнение в качестве разности:

( 3 x y 5 + 6 y 6 + 13 x 5 ) — ( 6 y 6 — x y 5 + 3 x 5 ) .

Далее раскрываем скобки: 3 x y 5 + 6 y 6 + 13 x 5 — 6 y 6 + x y 5 — 3 x 5 .

Стоит помнить, что если перед скобками находится знак минус, то в случае раскрытия скобок знаки поменяются на противоположные. Приводим подобные слагаемые, в итоге получаются:

4 x y 5 + 10 x 5 .

Получается, что в результате разности получается такой же многочлен.

Произведение многочлена и одночлена

В итоге умножения всегда получается только многочлен. Рассмотрим этапы умножения:

• составляют определенное произведение;
• раскрывают скобки;
• для раскрытия скобок в процессе умножения нужно сделать умножение каждого одночлена на каждый элемент многочлена, а также нужно сложить данные уравнения между собой;
• происходит группировка одних чисел с другими, одинаковых переменных друг с другом;
• происходит умножение чисел, а также складываются степени соответствующих одинаковых переменных.

Совершим умножение одночлена ( — m 2 n ) на многочлен ( m 2 n 2 — m 2 — n 2 ) .

Решение. Составляется произведение:

( — m 2 n ) × ( m 2 n 2 — m 2 — n 2 ) .

( — m 2 n ) × m 2 n 2 + ( — m 2 n ) × ( — m 2 ) + ( — m 2 n ) × ( — n 2 ) .

После умножения получится следующее выражение: — m 4 n 3 + m 4 n + m 2 n 3 .

Произведение двух многочленов

Представим правило умножения: нужно каждый элемент первого многочлена перемножить на каждый элемент второго многочлена, далее нужно произвести сложение полученных результатов, итоговый многочлен нужно привести к стандартному виду.

Произведением умножение многочлена на многочлен ( 1 — 4 x 2 ) и ( 5 y 2 — 3 x — 2 ) .

Нужно составить соответствующее произведение: ( 1 — 4 x 2 ) × ( 5 y 2 — 3 x — 2 ) .

Раскрываются скобки согласно правилу: 5 y 2 — 3 x — 2 — 20 x 2 y 2 + 12 x 3 + 8 x 2 .

Данный многочлен обладает стандартным видом, а, значит, ответом будет:

5 y 2 — 3 x — 2 — 20 x 2 y 2 + 12 x 3 + 8 x 2 .

Также возможно совершить деление, при котором можно перейти полностью к сокращению дроби (то есть перейти на уровень, когда дробь под чертой можно сократить).

Видео:Многочлены. 10 класс.Скачать

Каноническая форма многочлена

Стандартный многочлен степени m (полином) от одинарной переменной x — уравнение формы типа

a ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a m x m = ∑ i = 0 m a i x i ,

при котором a i ∈ K , a m ≠ 0 .

Часть a i является коэффициентами многочлена. Они могут являться нулевыми (как элементы, так и все полностью).

Можно определить каноническую форму многочлена таким образом: находится самое большое i.

Оно должно быть таким, чтобы a i ≠ 0 , допустим, i = n .

Получается следующее выражение: a ( x ) = a 0 + a 1 x 1 + a 2 x 2 + . . . a n x n , a n ≠ 0 .

Если абсолютно все a i стремятся к нулю, то каноническая форма будет нулем.

Число 0 ∈ K будет читаться многочленом с нулевыми коэффициентами, носит название нулевых многочленов. Однако степень нулевого многочлена является неопределенной.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Примеры решения задач для самостоятельного разбора новой темы

Представим задачу на многочлены от нескольких переменных

Умножить многочлены ( a 2 + b + 1 ) и ( a 2 — 24 b + 6 ) . Привести результат к стандартному виду.

Решение. Нужно составить выражение ( a 2 + b + 1 ) × ( a 2 — 24 b + 6 ) .

Раскрываем скобки согласно правилу: a 4 — 24 a 2 b + 6 a 2 + a 2 b — 24 b 2 + 6 b + a 2 — 24 b + 6 .

Приводим его к стандартному виду: a 4 — 23 a 2 b + 7 a 2 — 24 b 2 — 18 b + 6 .

Ответ: a 4 — 23 a 2 b + 7 a 2 — 24 b 2 — 18 b + 6 .

Видео:Многочлены от нескольких переменныхСкачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №13. Многочлены от нескольких переменных.

Перечень вопросов, рассматриваемых в теме

1) определение многочлена от нескольких переменных;

2) понятие симметрических многочленов;

3) формулы сокращенного умножения для старших степеней;

4) бином Ньютона;

5) метод неопределенных коэффициентов.

Глоссарий по теме

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.

Уравнение Р(x;y) = а, где , называютсимметрическим, если Р(х;y) — симметрический многочлен.

Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.

Пример 1. Разложить на множители многочлен: 2x 2 -5xy+2y 2 .

Воспользуемся методом группировки

2x 2 -5xy+2y 2= 2x 2 -4xy-xy+2y 2 = 2x(x-2y) –y(x-2y)=

Пример 2. Выведем формулу сокращенного умножения для «квадрата суммы» (x+y+z+u) 2 .

(x+y+z+u) 2 =((x+y)+(z+u)) 2 = (x+y) 2 +2(x+y)(z+u)+(z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).

Итак, мы получили (x+y+z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).

Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.

2) р(х; у)=3х 2 +5ху-7у 2 — однородный многочлен второй степени; соответственно 3х 2 +5ху-7у 2 =0 — однородное уравнение второй степени.

3) p(x; y)= x 3 +4xy 2 -5y 3 — однородный многочлен третьей степени; x 3 +4xy 2 -5y 3 =0 соответственно — однородное уравнение третьей степени.

4) p(x; y)= a_nx n +a_n-1x n-1 y+a_n-2x n-2 y 2 ₊…+a₁xy n-1 +a₀y n — общий вид однородного многочлена n-й степени.

Рассмотрим еще один метод разложения многочленов на множители-

метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения

1. Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
2. Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
3. Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Пример 3. Разложить на множители многочлен

3 x 3 – x 2 – 3 x + 1.

Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3 x 3 – x 2 – 3 x + 1 = ( x – p )( ax 2 + bx + c ) = ax 3 + ( b – ap ) x 2 + ( c – bp ) x – pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:

Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).

Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.

Пример 4. Решим уравнение x 3 +4xy 2 -5y 3 =0

Заметим, что если в заданном уравнении взять х=0, то получится у=0; это означает, что пара (0; 0) является решением однородного уравнения. Пусть теперь х. Разделим почленно обе части заданного однородного уравнения на х 3 , получим:

Введем новую переменную . Тогда уравнение примет вид 1+4z 2 -5z 3 =0.

Далее последовательно находим:

(5z 3 -5z 2 )+(z 2 -1)=0

Из уравнения z-1=0 находим z=1, уравнение 5z 3 -4z 2 -1=0 действительных корней не имеет.

Если z=1, то , т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.

Ответ: (t; t), где t- любое действительное число.

Теперь поговорим о симметрических многочленах. Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х. Например, симметрическим является двучлен x 2 y+xy 2 . В самом деле, при одновременной замене х на у и у на х получится двучлен y 2 x+yx 2 , но это то же самое, что x 2 y+xy 2 . Другие примеры симметрических многочленов: xy, x+y, x 2 +y 2 , x 3 +y 3 , x 4 +y 4 и т.д. Первые два из записанных многочленов считаются основными в том смысле, что любые другие симметрические многочлены можно представить в виде некоторой комбинации многочленов х + у и ху.

Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.

x 2 +y 2 =(x+y) 2 -2xy

x 3 +y 3 =(x+y) 3 -3xy(x+y)

x 4 +y 4 = 2xy(x 2 +y 2 )-(x 4 +y 4 )+3(xy) 2 и т.д.

Уравнение Р(x;y) = а, где , называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.

А теперь перейдем к такому понятию как бином Ньютона.

Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Бином Ньютона — название формулы, выражающей степень двучлена в виде суммы одночленов.

Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.

Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.

(a+b) 2 =a 2 +2ab+b 2

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах

Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?

Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):

(a+b) 4 =(a+b) 3 (a+b)=(a 3 +3a 2 b+3ab 2 +b 3 )(a+b)=a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4

(a+b) 5 =(a+b) 4 (a+b)=(a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 )(a+b)=a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +b 5

Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:

Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):

Общая формула бинома Ньютона:

.

Правая часть формулы называется разложением степени бинома.

— называется биномиальными коэффициентами, а все слагаемые — членами бинома.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

На самом деле, о треугольнике Паскаля было известно задолго до Паскаля — его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел (биномиальных коэффициентов) до n=12 включительно.

Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Доказать, что значение выражения 5 n +28n-1, где n – натуральное число, делится на 16 без остатка.

Решение: представим первое слагаемое выражение как 5 n = (4+1) n и воспользуемся формулой бинома Ньютона:

Полученное произведение доказывает делимость исходного выражения на 16.

Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница

Примеры и разборы решения заданий тренировочного модуля

Из данных многочленов выделите симметрические:

1. 2х 2 -5ху+2у 2 -6
2. 6x⁴-16xy²-6y 3 +19
3. -3ху+6х²-5у²+8
4. 16x 4 y²+16x²y 4 -x⁴-y⁴

Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.

1. 2х 2 -5ху+2у 2 -6
2. 6x⁴-16xy²-6y 3 +19
3. -3ху+6х²-5у²+8
4. 16x 4 y²+16x²y 4 -x⁴-y⁴

(а+b) 5 = __a 5 +___a 4 b+___a 3 b 2 +___a 2 b 3 +___ab 4 +__b 5

Решение: для решения данного задания воспользуемся треугольником Паскаля

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

Нас интересует последняя строчка.

Применив ее, получим ответ:

(а+b) 5 = 1a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +1b 5

Видео:Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Многочлены от нескольких переменных и алгоритм Бухбергера на Haskell

В этой статье я хочу рассказать о том, как реализовывал алгоритмы, связанные с базисами Грёбнера, на языке Haskell. Надеюсь, кому-нибудь мои идеи и объяснения окажутся полезными. Я не собираюсь вдаваться в теорию, так что читателю стоит быть знакомым с понятиями полиномиального кольца, идеала кольца и базиса идеала. Советую прочитать вот эту книгу МЦНМО, в ней подробно расписана вся необходимая теория.

Основной предмет статьи — базисы Грёбнера идеалов колец многочленов от нескольких переменных. Это понятие возникает при изучении систем полиномиальных уравнений. В конце статьи я на примере покажу, как можно применять эти идеи.

Самый главный результат, который даёт эта теория — хороший способ решать полиномиальные системы уравнений от нескольких переменных. Даже если вы не знакомы с высшей алгеброй или с Haskell, я советую вам прочитать эту статью, так как эти самые методы решения объяснены на уровне, доступном школьнику, а вся теория нужна только для обоснования. Можно спокойно пропустить всё, что связано с высшей алгеброй, и просто научиться решать системы уравнений.

Если вас заинтересовало, прошу под кат.

Я прошу прощения за картинки — это отрендерено latex’ом, а как заставить хабр понимать style=»width. ;height=. ;» я не знаю. Если подскажете способ лучше, обязательно переделаю.

1 Самые необходимые понятия из алгебры

Множества, на элементах которых можно задать две операции — «сложение» и «умножение», отвечающие определённому набору правил (аксиом), в алгебре называются кольцами. Многочлены от нескольких переменных, коэффициентами которых являются вещественные числа, образуют кольцо, обозначаемое , относительно обычных школьных операций сложения и умножения многочленов. Идеалом кольца называется такое его подмножество, разность двух элементов которого лежит в нём же и произведение любого его элемента и произвольного элемента кольца лежит в этом подмножестве. Самый простой пример идеала — множество кратных пяти чисел как идеал в кольце целых чисел. Самостоятельно убедитесь в том, что это идеал. Если получилось — дальше тоже особых проблем не возникнет.

Далее мы будем рассматривать только идеалы в кольце многочленов. Некоторый конечный набор многочленов называется базисом идеала, если любой многочлен из идеала представим в виде , где — какие-то многочлены. Этот факт записывается так: . Теорема Гильберта о базисе даёт замечательный результат — любой идеал (в кольце многочленов) имеет конечный базис. Это позволяет работать в любой ситуации просто работать с конечными базисами идеалов.

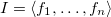
Теперь будем рассматривать системы уравнений следующего вида:

Назовём идеалом этой системы идеал 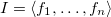. Из алгебры известно, что любой многочлен, лежащий в идеале , обращается в нуль на любом решении исходной системы. И далее, если — другой базис идеала , то система

имеет то же множество решений, что и исходная. Из этого всего следует, что если нам удастся найти в идеале системы базис, который проще, чем исходный, то и задача решения самой системы упрощается.

Волшебным образом такой базис существует — он называется базисом Грёбнера идеала. По определению это такой базис, что процедура деления с остатком (о ней позже) для любого многочлена из идеала выдаст нулевой остаток. Если произвести его построение, то один из его многочленов, по крайней мере в большинстве случаев, будет зависеть только от одной переменной, что позволит решить и всю систему последовательной подстановкой.

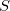
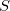
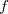
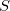
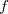
Последнее, что нам понадобится — -полином и критерий -пар Бухбергера. Выберем какой-нибудь «хороший» способ упорядочивания одночленов (за подробностями — в книжку) и обозначим через старший член (относительно этого упорядочивания) многочлена , а через — наименьшее общее кратное одночленов и . Тогда -полиномом от и называется следующая конструкция:

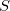
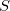
Доказано (критерий -пар), что базис идеала является его базисом Грёбнера тогда и только тогда, когда -многочлен от любой пары его членов даёт остаток 0 при делении на базис (как это делается будет объяснено далее). Это тут же подсказывает алгоритм построения такого базиса:

1. Для каждой пары многочленов базиса составить их -многочлен и разделить его с остатком на базис.
2. Если все остатки равны нулю, получен базис Грёбнера. Иначе, добавить все ненулевые остатки к базису и вернуться на шаг 1.

Это и есть алгоритм Бухбергера — основной предмет этой статьи. На этом с математикой всё, можно переходить. Если вы что-то не поняли, стоит посмотрите википедию или книгу, хотя дальнейшее повествование не требует знаний высшей алгебры.

2 Представление многочленов от нескольких переменных на Haskell

Начнём строить представление многочленов с одночленов. Одночлен характеризуется всего двумя вещами — коэффициентом и набором степеней переменных. Будем считать, что имеются переменные , и так далее. Тогда одночлен имеет коэффициент 1 и степени [2,3,1] , а одночлен — коэффициент 2 и степени [0,0,3] . Обратите внимание на нулевые степени! Они критичны для реализации всех остальных методов. Вообще, потребуем, чтобы списки степеней всех одночленов (в рамках одной задачи) имели одинаковую длину. Это значительно упростит нам работу.

Опишем тип «одночлен» как алгебраический тип данных, состоящий из коэффициента (типа « c ») и списка степеней (каждая типа « a »):

Нам потребуется сравнивать между собой одночлены, так что самое время написать воплощение класса Ord . Я буду использовать обычное лексикографическое упорядочение по степеням, так как оно очень просто и вместе с тем соответствует правилам «хорошего» упорядочения одночленов. Также напишем воплощение класса Show просто для удобства работы с нашей системой.

Функция show пытается быть «умной»: она не показывает коэффициент, если он равен 1, и она не показывает переменные нулевой степени, а так же не показывает первую степень переменных. Вот так:

Я буду писать функции, похожие на show , постоянно, так что стоит пояснить, как именно она работает — уверен, кого-нибудь она точно испугала. С помощью zip as [1..] склеиваем каждую степень с номером своей переменной, затем с помощью filter (
(p _) -> p /= 0) избавляемся от нулевых степеней, превращаем описание каждой переменной в строку через showOne и, наконец, склеиваем всё вместе, перемежая значками умножения, используя intercalate из Data.List

Теперь мы готовы описать собственно тип многочленов. Для этого подойдёт newtype обёртка над обычным списком:

На этот раз функция show простая, так как вся грязная работа уже спрятана в типе одночленов. Работает это так:

Договоримся на будущее, что одночлены в этом списке всегда будут храниться в порядке убывания (в смысле нашего определения воплощения Ord ). Это позволит реализовать некоторые вещи гораздо проще.

3 Операции над многочленами

Самые простые операции это LT, проверки на равенство нулю и умножение на число. Из нашего соглашения об упорядоченности мономов следует, что старший моном всегда стоит на первом месте в списке и может быть получен с помощью head . Одночлен считается нулевым в том случае, если его коэффициент равен нулю, а многочлен — если он не содержит одночленов. Ну а умножение на константу просто изменяет коэффициент:

Два одночлена будут называться подобными, если они отличаются только коэффициентами. Для них определена сумма — нужно просто сложить коэффициенты, а степени оставить без изменения.

Чтобы перемножить два одночлена, просто сложим степени каждой из переменных. Эту операция очень легко реализовать с помощью замечательной функции zipWith . Я думаю, код говорит сам за себя:

Гораздо более интересно сложение многочленов. Будем решать эту задачу рекурсивно. Тривиальные случаи — сумма двух нулевых многочлена (пустых списков) равна нулевому многочлену. Сумма любого многочлена и нулевого равна ему же. Теперь мы можем считать оба многочлена ненулевыми, а значит каждый из них можно разделить на старший член и остальные — «хвост». Возникает два случая:

1. Старшие члены подобны. В этом случае сложим их и добавим результат (если он ненулевой) к сумме хвостов.
2. Старшие члены не подобны. Тогда выберем больший из них. Наше условие упорядоченности гарантирует, что в хвостах обоих многочленов не найдётся подобного ему одночлена. Следовательно, мы можем сложить хвост выбранного многочлена с другим, а затем добавить в его начало этот самый больший одночлен.

Остаётся заметить, что в результате этой рекурсивной процедуры снова получится упорядоченный многочлен, и написать, собственно код.

Умножение многочленов получается абсолютно естественным путём. Очень просто умножить одночлен на многочлен — просто умножим его на каждый из одночленов с помощью map и mulMono . А затем применим дистрибутивность («распределительный закон», раскрытие скобок) к произведению двух многочленов и получим, что требуется лишь умножить все одночлены первого полинома на второй и сложить полученные результаты. Умножения выполним с помощью всё того же map , а результаты сложим, воспользовавшись foldl’ и addPoly . Код этих двух операций получился на удивление коротким — короче, чем описания типов!

Вот и всё, мы реализовали основные действия над многочленами, а значит можно двигаться дальше!

4 Деление с остатком на базис (редукция)

Будем говорить, что одночлен делится на одночлен , если существует такой одночлен , что . Очевидно, что это верно, только если каждая переменная входит в в не меньшей степени, чем в . Следовательно, проверку на делимость можно реализовать с помощью уже знакомой функции zipWith и замечательной функции and . А вместе с проверкой легко получить и собственно процедуру деления:

Обратите внимание, что теперь тип коэффициента должен позволять деление — класс Fractional . Это удручает, но ничего не поделаешь.
Алгоритм деления многочлена на базис с остатком это, по существу, простое школьное деление столбиком. Среди многочленов базиса выбирается первый такой полином, что на его старший член делится старший член делимого, затем из делимого вычитается этот полином, умноженный на частное их старших членов. Результат вычитания принимается за новое делимое и процесс повторяется. Если старший член не делится ни на один из старших членов базиса, деление завершается и последнее делимое называется остатком.

Нашей основной процедуре деления, назовём её reduceMany , потребуются две вспомогательных — reducable и reduce . Первая из них проверяет, делится ли многочлен на другой, а вторая осуществляет деление.

Так как у нас нет функции для вычитания, просто умножим второй многочлен на -1 и сложим их — всё просто! А вот и весь алгоритм деления:

Функция reduceMany пытается поделить многочлен на базис. Если деление произошло, процесс продолжается, иначе — завершается. Внутренняя функция reduceStep всего лишь ищет тот самый первый многочлен, на который можно поделить, и делит, возвращая остаток и флаг, показывающий, было ли сделано деление.

5 Алгоритм Бухбергера

Вот мы и подошли к основной части этой статьи — реализации алгоритма Бухбергера. Единственное, чего у нас ещё нет, это функции для получения 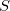-полинома. Её реализация очень проста, как и вспомогательной функции для поиска наименьшего общего кратного одночленов:

Здесь оба полинома просто умножаются на соответствующие одночлены, причём второй дополнительно ещё и на минус единицу, как и в случае деления с остатком.
Я уверен, что существует множество способов реализовать этот алгоритм. Я также не претендую на то, что моя реализация достаточно оптимальна или проста. Но она мне нравится и она работает, и это всё, что требуется.

Подход, который я использовал, можно назвать динамическим. Разделим наш базис на две части — ту, в которой мы уже проверили (и добавили) 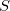-полиномы от всех пар — « checked » — и ту, в которой только предстоит сделать это — « add ». Один шаг алгоритма будет выглядеть так:

1. Возьмём первый многочлен из второй части
2. Последовательно построим -полиномы между ним и всеми многочленами первой части и добавим все ненулевые остатки в конец второй части
3. Переместим этот многочлен в первую часть

Как только вторая часть окажется пустой, первая будет содержать базис Грёбнера. Преимущество такого решения в том, что не будут считаться 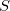-полиномы от тех пар, от которых они уже посчитаны и проверены. Ключевая функция в этом процессе — checkOne . Она принимает многочлен (из второй части), а так же обе части, а возвращает список многочленов, которые следует добавить к базису. Используем простую рекурсию по первой части, естественно не добавляя нулевые остатки:

Наверняка это можно заменить на хитрый foldl , но я оставлю это в качестве упражнения. Осталось лишь построить сам базис Грёбнера по данному. Реализация шага алгоритма дословно повторяет его описание, смотрите сами:

Многочлен a переходит в первую часть, а во вторую попадают все его ненулевые остатки. Обратите внимание, что и правда достаточно проверять -полиномы каждого многочлена второй части только с первой, в силу перемещений полиномов между частями. Остаётся заметить, что для получения базиса Грёбнера из данного достаточно поместить один его многочлен в первую часть, остальные — во вторую и применить процедуру build , что и сделано в функции makeGroebner .

6 Примеры использования

Все эти теоретические построения кажутся совершенно бесполезными без демонстрации практического применения этих методов. В качестве примера рассмотрим задачу нахождения точки пересечения трёх окружностей — простейший случай позиционирования на карте. Запишем уравнения окружностей как систему уравнений:

.

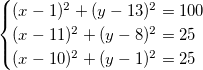
После раскрытия скобок получаем следующее:

Построим базис Грёбнера (я использовал тип Rational для пущей точности):

Чудесным образом мы получили два линейных уравнения, которые быстро дают ответ — точка (7,5). Можно проверить, что она лежит на всех трёх окружностях. Итак, мы свели решение системы трёх сложных квадратных уравнений к двум простым линейным. Базисы Грёбнера — действительно полезный инструмент для подобных задач.

7 Вопросы для размышления и заключение

На самом деле, этот результат можно ещё улучшить. -полиномы требуется считать только для тех пар многочленов, старшие члены которых не взаимно просты — то есть их наименьшее общее кратное не является просто их произведением. В некоторых источниках про этот случай говорят «многочлены имеют зацепление». Добавьте такую оптимизацию в нашу функцию makeGroebner .

Если в итоговый базис попал полином, старший член которого делится на старший член какого-то другого полинома из базиса, то его можно исключить. Базис, полученный после исключения всех таких многочленов, называется минимальным базисом Грёбнера. Также можно рассмотреть полином, произвольный член которого делится на старший член какого-то другого полинома. В этом случае заменим этот полином остатком от деления на другой. Базис, в котором проведены все возможные операции такого типа, называется редуцированным. В качестве упражнения реализуйте минимизацию и редуцирование базиса.

В заключение хочу сказать спасибо всем, кто дочитал эту статью до конца. Я знаю, что моё повествование было несколько сумбурным, а код неидеальным (и, может, непонятным), но я всё-таки надеюсь, что заинтересовал кого-нибудь базисами Грёбнера. Мне будет очень приятно, если кто-нибудь сможет найти применение моим наработкам в хоть сколько-нибудь реальных задачах.

📹 Видео

Схема Горнера. 10 класс.Скачать

Школьная математика. Симметрические многочлены от двух переменных. Часть 1.Скачать

МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 1Скачать

Многочлены от нескольких переменных. Однородные многочлены. Симметрические многочленыСкачать

Многочлены. 7 класс.Скачать

✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Математика. Многочлены с несколькими переменными. Видеоурок 1. Шварц А.В.Скачать

Деление многочленов | Математика | TutorOnlineСкачать

Теорема Безу и разложение многочлена на множителиСкачать

11 класс, 1 урок, Многочлены от одной переменнойСкачать

ЕГЭ по математике. Деление многочлена на двучленСкачать

Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать